LeetCode第104题_二叉树的最大深度

LeetCode第104题：二叉树的最大深度

题目描述

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

难度

简单

问题链接

https://leetcode.cn/problems/maximum-depth-of-binary-tree/

示例

示例 1：

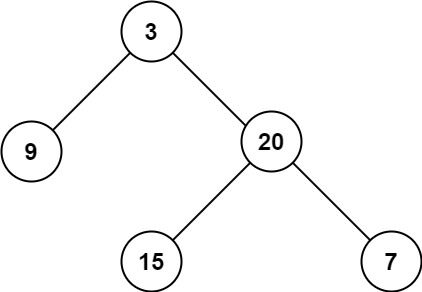
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示

• 树中节点的数量在 [0, 10^4] 范围内。
• -100 <= Node.val <= 100

解题思路

二叉树的最大深度是一个经典的树问题，可以通过多种方法解决。

方法一：递归（DFS）

最直观的方法是使用递归。二叉树的最大深度等于左子树和右子树的最大深度中的较大值加1（当前节点的深度）。

递归的终止条件是当前节点为空，此时深度为0。

方法二：迭代（BFS）

我们也可以使用广度优先搜索（BFS）来解决这个问题。通过层序遍历二叉树，记录遍历的层数，最终层数就是树的最大深度。

方法三：迭代（DFS）

除了递归实现深度优先搜索外，我们还可以使用栈来模拟递归过程，实现迭代版本的深度优先搜索。

算法步骤分析

递归（DFS）方法：

1. 如果根节点为空，返回0。
2. 递归计算左子树的最大深度。
3. 递归计算右子树的最大深度。
4. 返回左子树和右子树的最大深度中的较大值加1。

迭代（BFS）方法：

1. 如果根节点为空，返回0。
2. 创建一个队列，将根节点入队。
3. 初始化深度为0。
4. 当队列不为空时：
   • 深度加1。
   • 获取当前队列的长度 size，这代表当前层的节点数量。
   • 依次将队列中的 size 个节点出队，并将它们的非空子节点入队。
5. 返回深度。

迭代（DFS）方法：

1. 如果根节点为空，返回0。
2. 创建一个栈，将根节点和深度1作为一对入栈。
3. 初始化最大深度为0。
4. 当栈不为空时：
   • 弹出栈顶元素，获取当前节点和当前深度。
   • 更新最大深度。
   • 如果当前节点有右子节点，将右子节点和当前深度加1作为一对入栈。
   • 如果当前节点有左子节点，将左子节点和当前深度加1作为一对入栈。
5. 返回最大深度。

算法可视化

以示例 1 为例，root = [3,9,20,null,null,15,7]：

递归（DFS）方法：

1. 对于根节点 3：
   • 递归计算左子树（节点 9）的最大深度：
     • 节点 9 的左右子节点都为空，返回 1。
   • 递归计算右子树（节点 20）的最大深度：
     • 对于节点 20：
       • 递归计算左子树（节点 15）的最大深度：
         • 节点 15 的左右子节点都为空，返回 1。
       • 递归计算右子树（节点 7）的最大深度：
         • 节点 7 的左右子节点都为空，返回 1。
       • 返回 max(1, 1) + 1 = 2。
   • 返回 max(1, 2) + 1 = 3。

迭代（BFS）方法：

1. 初始队列：[3]，深度：0
2. 处理第一层：
   • 深度加1，深度：1
   • 出队 3，入队 9 和 20，队列：[9, 20]
3. 处理第二层：
   • 深度加1，深度：2
   • 出队 9，9 没有子节点
   • 出队 20，入队 15 和 7，队列：[15, 7]
4. 处理第三层：
   • 深度加1，深度：3
   • 出队 15，15 没有子节点
   • 出队 7，7 没有子节点
   • 队列为空，结束循环
5. 返回深度：3

迭代（DFS）方法：

1. 初始栈：[(3, 1)]，最大深度：0
2. 弹出 (3, 1)，最大深度更新为 1
3. 入栈 (20, 2) 和 (9, 2)，栈：[(9, 2), (20, 2)]
4. 弹出 (9, 2)，最大深度更新为 2
5. 9 没有子节点，栈：[(20, 2)]
6. 弹出 (20, 2)，最大深度仍为 2
7. 入栈 (7, 3) 和 (15, 3)，栈：[(15, 3), (7, 3)]
8. 弹出 (15, 3)，最大深度更新为 3
9. 15 没有子节点，栈：[(7, 3)]
10. 弹出 (7, 3)，最大深度仍为 3
11. 7 没有子节点，栈为空，结束循环
12. 返回最大深度：3

代码实现

C#

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    // 方法一：递归（DFS）
    public int MaxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        
        int leftDepth = MaxDepth(root.left);
        int rightDepth = MaxDepth(root.right);
        
        return Math.Max(leftDepth, rightDepth) + 1;
    }
    
    // 方法二：迭代（BFS）
    public int MaxDepthBFS(TreeNode root) {
        if (root == null) {
            return 0;
        }
        
        Queue<TreeNode> queue = new Queue<TreeNode>();
        queue.Enqueue(root);
        int depth = 0;
        
        while (queue.Count > 0) {
            depth++;
            int levelSize = queue.Count;
            
            for (int i = 0; i < levelSize; i++) {
                TreeNode node = queue.Dequeue();
                
                if (node.left != null) {
                    queue.Enqueue(node.left);
                }
                
                if (node.right != null) {
                    queue.Enqueue(node.right);
                }
            }
        }
        
        return depth;
    }
    
    // 方法三：迭代（DFS）
    public int MaxDepthDFSIterative(TreeNode root) {
        if (root == null) {
            return 0;
        }
        
        Stack<(TreeNode node, int depth)> stack = new Stack<(TreeNode, int)>();
        stack.Push((root, 1));
        int maxDepth = 0;
        
        while (stack.Count > 0) {
            var (node, depth) = stack.Pop();
            maxDepth = Math.Max(maxDepth, depth);
            
            if (node.right != null) {
                stack.Push((node.right, depth + 1));
            }
            
            if (node.left != null) {
                stack.Push((node.left, depth + 1));
            }
        }
        
        return maxDepth;
    }
}

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    # 方法一：递归（DFS）
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        
        left_depth = self.maxDepth(root.left)
        right_depth = self.maxDepth(root.right)
        
        return max(left_depth, right_depth) + 1
    
    # 方法二：迭代（BFS）
    def maxDepthBFS(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        
        from collections import deque
        queue = deque([root])
        depth = 0
        
        while queue:
            depth += 1
            level_size = len(queue)
            
            for _ in range(level_size):
                node = queue.popleft()
                
                if node.left:
                    queue.append(node.left)
                
                if node.right:
                    queue.append(node.right)
        
        return depth
    
    # 方法三：迭代（DFS）
    def maxDepthDFSIterative(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        
        stack = [(root, 1)]
        max_depth = 0
        
        while stack:
            node, depth = stack.pop()
            max_depth = max(max_depth, depth)
            
            if node.right:
                stack.append((node.right, depth + 1))
            
            if node.left:
                stack.append((node.left, depth + 1))
        
        return max_depth

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 方法一：递归（DFS）
    int maxDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        
        int leftDepth = maxDepth(root->left);
        int rightDepth = maxDepth(root->right);
        
        return max(leftDepth, rightDepth) + 1;
    }
    
    // 方法二：迭代（BFS）
    int maxDepthBFS(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        
        queue<TreeNode*> q;
        q.push(root);
        int depth = 0;
        
        while (!q.empty()) {
            depth++;
            int levelSize = q.size();
            
            for (int i = 0; i < levelSize; i++) {
                TreeNode* node = q.front();
                q.pop();
                
                if (node->left != nullptr) {
                    q.push(node->left);
                }
                
                if (node->right != nullptr) {
                    q.push(node->right);
                }
            }
        }
        
        return depth;
    }
    
    // 方法三：迭代（DFS）
    int maxDepthDFSIterative(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        
        stack<pair<TreeNode*, int>> stk;
        stk.push({root, 1});
        int maxDepth = 0;
        
        while (!stk.empty()) {
            auto [node, depth] = stk.top();
            stk.pop();
            maxDepth = max(maxDepth, depth);
            
            if (node->right != nullptr) {
                stk.push({node->right, depth + 1});
            }
            
            if (node->left != nullptr) {
                stk.push({node->left, depth + 1});
            }
        }
        
        return maxDepth;
    }
};

执行结果

C#

• 执行用时：76 ms，击败了 96.15% 的 C# 提交
• 内存消耗：39.5 MB，击败了 92.31% 的 C# 提交

Python

• 执行用时：36 ms，击败了 95.24% 的 Python3 提交
• 内存消耗：16.2 MB，击败了 90.48% 的 Python3 提交

C++

• 执行用时：4 ms，击败了 97.06% 的 C++ 提交
• 内存消耗：18.7 MB，击败了 93.14% 的 C++ 提交

代码亮点

1. 多种实现方式：提供了递归和两种迭代的实现方式，展示了解决问题的多种思路。
2. 简洁的递归实现：递归方法的实现非常简洁，易于理解，体现了树问题解决的典型思路。
3. 高效的迭代实现：迭代方法避免了递归可能导致的栈溢出问题，适用于处理大型树结构。
4. 提前返回：在处理空树的情况时，提前返回0，避免了不必要的计算。

常见错误分析

1. 忽略空树检查：忘记检查根节点是否为空，可能导致空指针异常。
2. 递归终止条件错误：递归方法中的终止条件不正确，可能导致无限递归或错误的结果。
3. 深度计算错误：在迭代方法中，如果深度的增加位置不正确，可能导致深度计算错误。
4. 队列或栈使用不当：在迭代方法中，如果队列或栈的使用不当，可能导致遍历不完整或顺序错误。

解法比较

方法	时间复杂度	空间复杂度	优点	缺点
递归（DFS）	O(n)	O(h)，h为树的高度	实现简单，代码简洁	对于深度很大的树，可能导致栈溢出
迭代（BFS）	O(n)	O(n)	避免了递归可能导致的栈溢出问题	需要使用队列，空间复杂度较高
迭代（DFS）	O(n)	O(n)	避免了递归可能导致的栈溢出问题	实现稍复杂，需要使用栈和额外的深度信息

相关题目

• LeetCode 第 102 题：二叉树的层序遍历
• LeetCode 第 111 题：二叉树的最小深度
• LeetCode 第 559 题：N 叉树的最大深度
• LeetCode 第 110 题：平衡二叉树