中频信号解析:瞬时相位信息的原理与应用
中频信号解析:瞬时相位信息的原理与应用
引言
在雷达信号处理(图1)、数字通信系统等工程领域,瞬时相位作为信号时频分析的核心参数,承载着调制信息解调、目标特征提取等关键功能。本文将从数学原理、信号处理价值、典型应用三个维度深入剖析瞬时相位的本质。
一、瞬时相位的基本概念
瞬时相位是描述信号在某一时刻相位状态的重要参数,反映了信号在时间-频率域中的动态特性。在信号处理中,瞬时相位可通过解析信号(Analytic Signal)来定义。对于一个实信号 x ( t ) x(t) x(t),其解析信号 z ( t ) z(t) z(t) 由原始信号和其希尔伯特变换(Hilbert Transform)构成:
z ( t ) = x ( t ) + j ⋅ H [ x ( t ) ] z(t) = x(t) + j \cdot \mathcal{H}[x(t)] z(t)=x(t)+j⋅H[x(t)]
其中,希尔伯特变换 H [ x ( t ) ] \mathcal{H}[x(t)] H[x(t)] 将信号的正频率分量相位延迟 9 0 ∘ 90^{\circ} 90∘ ,负频率分量相位超前 9 0 ∘ 90^{\circ} 90∘ 。瞬时相位 ϕ ( t ) \phi(t) ϕ(t) 则定义为解析信号的幅角:
ϕ ( t ) = arctan ( H [ x ( t ) ] x ( t ) ) \phi(t) = \arctan\left( \frac{\mathcal{H}[x(t)]}{x(t)} \right) ϕ(t)=arctan(x(t)H[x(t)])
物理意义:
瞬时相位可以表征信号的局部周期性特征。例如,在调频信号中,瞬时相位的变化率直接对应瞬时频率,即:
f ( t ) = 1 2 π d ϕ ( t ) d t f(t) = \frac{1}{2\pi} \frac{d\phi(t)}{dt} f(t)=2π1dtdϕ(t)
该关系式在频率调制信号解调中具有重要应用价值。
二、瞬时相位在信号处理中的作用
1. 动态特征提取
瞬时相位能够捕捉信号的非平稳特性,如频率调制(FM)信号的频率变化规律。在雷达系统中,目标微小位移(如1mm)会导致中频信号相位变化 18 0 ∘ 180^{\circ} 180∘,通过相位差计算可实现高精度测距和测速。
2. 噪声鲁棒性
相比直接分析信号幅度,相位信息对加性噪声更鲁棒。例如,在机械故障诊断中,即使信号被噪声污染,瞬时相位仍能有效反映轴承的振动特征。
3. 多分量信号分离
通过相位建模法(Phase Modeling)和时频分布(如Wigner-Ville分布),可将混合信号分解为多个单分量信号,分别分析其瞬时相位。
三、瞬时相位的数学推导与MATLAB实现
案例:调频信号的瞬时相位计算
设调频信号为 s ( t ) = cos ( 2 π f c t + β sin ( 2 π f m t ) ) s(t) = \cos(2\pi f_c t + \beta \sin(2\pi f_m t)) s(t)=cos(2πfct+βsin(2πfmt)),其中 β \beta β为调制指数。其瞬时相位为:
ϕ ( t ) = 2 π f c t + β sin ( 2 π f m t ) \phi(t) = 2\pi f_c t + \beta \sin(2\pi f_m t) ϕ(t)=2πfct+βsin(2πfmt)
MATLAB代码实现:
fs = 1000; % 采样率
t = 0:1/fs:1; % 时间序列
fc = 10; fm = 2; beta = 5; % 载频、调制频率、调制指数
% 生成调频信号
s = cos(2*pi*fc*t + beta*sin(2*pi*fm*t));
% 计算瞬时相位
analytic_signal = hilbert(s); % 希尔伯特变换得到解析信号
phase = angle(analytic_signal); % 提取瞬时相位
% 可视化
figure();
subplot(2,1,1);
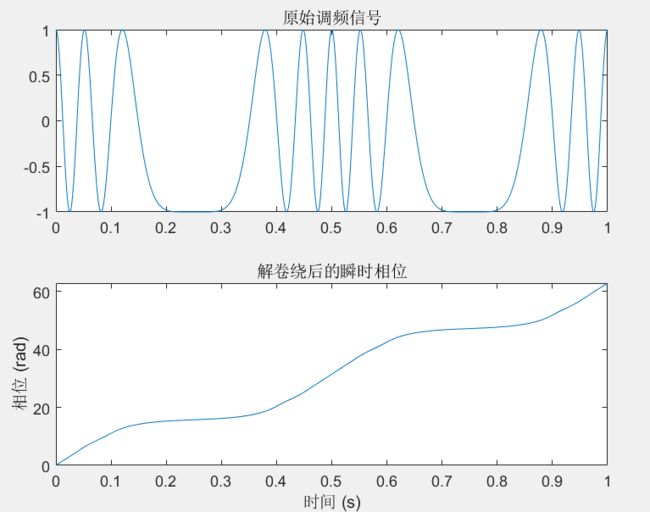
plot(t, s);
title('原始调频信号');
subplot(2,1,2);
plot(t, unwrap(phase));
xlabel('时间 (s)');
ylabel('相位 (rad)');
title('解卷绕后的瞬时相位');
代码说明:
-
hilbert函数生成解析信号,angle提取相位,unwrap消除相位跳变。 -
解卷绕(Unwrapping)处理可避免 ±π±π 的相位跳变,得到连续相位曲线 。
四、实际应用场景
- 雷达测速与测距
在FMCW雷达中,通过比较连续Chirp信号的相位差 Δ ϕ = 4 π d λ Δϕ=\frac{4πd}{λ} Δϕ=λ4πd,可精确计算目标距离 d d d;相位随时间的变化率 Δ ϕ Δ t \frac{Δϕ}{Δt} ΔtΔϕ用于估计速度 。 - 机械故障诊断
轴承振动信号的瞬时相位可反映故障特征频率。通过分析相位突变点,可定位损伤位置。 - 通信系统调制解调
在QPSK、QAM等数字调制中,瞬时相位携带符号信息。接收端通过相位解调恢复原始数据 。
五、扩展讨论:相位建模法
相位建模法通过多项式拟合瞬时相位的变化规律,适用于非平稳信号分析。设信号模型为:
ϕ ( t ) = a 0 + a 1 t + a 2 t 2 + ⋅ ⋅ ⋅ + a n t n ϕ(t) = a_0 +a_1t+a_2t^2+···+a_nt^n ϕ(t)=a0+a1t+a2t2+⋅⋅⋅+antn
利用最小二乘法估计系数 a i a_i ai,可分离多分量信号的相位。MATLAB实现可参考瞬时频率估计的相位建模法代码包 。
六、总结
瞬时相位是信号时频分析的核心参数,通过希尔伯特变换和相位建模法,可深入挖掘非平稳信号的动态特性。其在雷达、通信、故障诊断等领域具有广泛应用,结合MATLAB工具可实现高效算法验证。
六、总结
瞬时相位是信号时频分析的核心参数,通过希尔伯特变换和相位建模法,可深入挖掘非平稳信号的动态特性。其在雷达、通信、故障诊断等领域具有广泛应用,结合MATLAB工具可实现高效算法验证。