深度分离卷积模块：轻量化网络的革命性设计

引言：卷积神经网络的计算瓶颈

在计算机视觉领域，卷积神经网络(CNN)已经成为了事实上的标准架构。从AlexNet到ResNet，再到EfficientNet，CNN架构不断演进，在图像分类、目标检测和语义分割等任务上取得了令人瞩目的成绩。然而，随着模型性能的提升，网络的计算复杂度和参数量也呈指数级增长，这给移动端和嵌入式设备的部署带来了巨大挑战。

传统的标准卷积操作在提取特征时，同时考虑了空间相关性和通道相关性。这种"全功能"的设计虽然强大，但也带来了巨大的计算开销。深度分离卷积(Depthwise Separable Convolution)的提出，正是为了解决这一计算瓶颈，它通过将空间滤波和通道组合这两个操作分离，大幅减少了计算量和参数数量，同时保持了良好的特征提取能力。

本文将深入探讨深度分离卷积模块的设计原理、数学表达、实现细节以及在各种网络架构中的应用，帮助读者全面理解这一轻量化网络设计的核心技术。

第一部分：深度分离卷积的基本原理

1.1 标准卷积的计算代价

在深入理解深度分离卷积之前，我们需要先回顾标准卷积的操作方式及其计算成本。对于一个输入特征图F∈R^(H×W×C_in)，标准卷积使用一个卷积核K∈R^(k×k×C_in×C_out)对其进行操作，其中k是卷积核大小(通常为3或5)，C_in和C_out分别是输入和输出通道数。

标准卷积的计算量为：
FLOPs = H × W × C_in × C_out × k × k

参数量为：
Params = C_in × C_out × k × k

可以看出，计算量和参数量都与输入输出通道数的乘积成正比，当网络深度增加时，这会成为严重的计算瓶颈。

1.2 深度分离卷积的分解思想

深度分离卷积的核心思想是将标准卷积分解为两个独立的操作：深度卷积(Depthwise Convolution)和逐点卷积(Pointwise Convolution)。这种分解基于一个观察：标准卷积同时执行空间滤波和通道组合，而这两个功能可以分开进行。

深度卷积：对每个输入通道单独应用空间卷积滤波。与标准卷积不同，深度卷积不会跨通道组合信息，每个通道有自己的滤波器。数学上，这相当于使用C_in个k×k×1的滤波器，每个滤波器处理对应的输入通道。

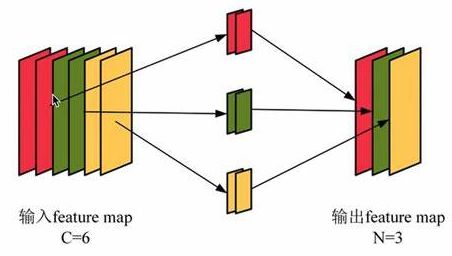
逐点卷积：使用1×1卷积来组合深度卷积输出的通道。这一步负责建立通道间的相关性，将C_in个通道线性组合为C_out个通道。

1.3 计算量对比

深度分离卷积的总计算量为深度卷积和逐点卷积之和：

FLOPs_depthwise = H × W × C_in × k × k
FLOPs_pointwise = H × W × C_in × C_out
Total FLOPs = H × W × C_in × (k × k + C_out)

与标准卷积相比，计算量减少了约：
Reduction = (k × k × C_out) / (k × k + C_out)倍

当C_out较大时(通常如此)，这个比值接近k²。对于3×3卷积，理论计算量减少约8-9倍。

第二部分：深度分离卷积的数学表达与实现

2.1 数学形式化表达

设输入特征图F∈R^(H×W×C_in)，标准卷积可以表示为：

(F*K)(x,y,c_out) = ∑(i,j=0)^(k-1) ∑(c_in=1)^C_in F(x+i,y+j,c_in) · K(i,j,c_in,c_out)

深度分离卷积将其分解为：

1. 深度卷积：
   (F*K_d)(x,y,c_in) = ∑_(i,j=0)^(k-1) F(x+i,y+j,c_in) · K_d(i,j,c_in)
   其中K_d∈R^(k×k×C_in)，每个输入通道有独立的空间滤波器

2. 逐点卷积：
   (F_p*K_p)(x,y,c_out) = ∑_(c_in=1)^C_in F_p(x,y,c_in) · K_p(0,0,c_in,c_out)
   其中F_p是深度卷积输出，K_p∈R^(1×1×C_in×C_out)

2.2 PyTorch实现示例

import torch
import torch.nn as nn

class DepthwiseSeparableConv(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
        super().__init__()
        self.depthwise = nn.Conv2d(
            in_channels, 
            in_channels, 
            kernel_size=kernel_size,
            stride=stride,
            padding=padding,
            groups=in_channels  # 关键参数，确保每个输入通道有自己的滤波器
        )
        self.pointwise = nn.Conv2d(
            in_channels,
            out_channels,
            kernel_size=1
        )
        
    def forward(self, x):
        x = self.depthwise(x)
        x = self.pointwise(x)
        return x

2.3 分组卷积的视角

深度卷积可以视为分组卷积的一种极端形式，其中分组数等于输入通道数。类似地，逐点卷积就是分组数为1的1×1卷积。这种视角有助于理解深度分离卷积在现有深度学习框架中的实现方式。

第三部分：深度分离卷积的变体与改进

3.1 带扩张率的深度分离卷积

为了在不增加计算量的情况下扩大感受野，可以在深度卷积中引入扩张率(dilation rate)：

nn.Conv2d(
    in_channels, 
    in_channels,
    kernel_size=3,
    dilation=2,  # 扩张率
    padding=2,   # 保持空间尺寸
    groups=in_channels
)

这种设计在语义分割任务中特别有用，可以在保持计算效率的同时捕获更大范围的上下文信息。

3.2 深度分离卷积与残差连接

将深度分离卷积与残差连接结合，可以构建更深的轻量化网络：

class DSResidualBlock(nn.Module):
    def __init__(self, channels, stride=1):
        super().__init__()
        self.conv = nn.Sequential(
            DepthwiseSeparableConv(channels, channels, 3, stride, 1),
            nn.BatchNorm2d(channels),
            nn.ReLU(),
            DepthwiseSeparableConv(channels, channels, 3, 1, 1),
            nn.BatchNorm2d(channels)
        )
        self.shortcut = nn.Sequential()
        if stride != 1:
            self.shortcut = nn.Sequential(
                nn.Conv2d(channels, channels, 1, stride),
                nn.BatchNorm2d(channels)
            )
            
    def forward(self, x):
        out = self.conv(x)
        out += self.shortcut(x)
        out = F.relu(out)
        return out

3.3 线性瓶颈与倒残差结构

MobileNetV2引入了线性瓶颈和倒残差结构，进一步优化了深度分离卷积：

1. 线性瓶颈：在残差块的最后一个1×1卷积后不使用ReLU激活，避免低维空间中的信息损失

倒残差：先使用1×1卷积扩展通道数，再进行深度卷积，最后用1×1卷积压缩通道数

class InvertedResidual(nn.Module):
    def __init__(self, in_channels, out_channels, stride, expand_ratio):
        super().__init__()
        hidden_dim = in_channels * expand_ratio
        self.use_residual = stride == 1 and in_channels == out_channels
        
        layers = []
        if expand_ratio != 1:
            layers.append(
                nn.Conv2d(in_channels, hidden_dim, 1, bias=False)
            )
            layers.append(nn.BatchNorm2d(hidden_dim))
            layers.append(nn.ReLU6())
            
        layers.extend([
            nn.Conv2d(hidden_dim, hidden_dim, 3, stride, 1, 
                      groups=hidden_dim, bias=False),
            nn.BatchNorm2d(hidden_dim),
            nn.ReLU6(),
            nn.Conv2d(hidden_dim, out_channels, 1, bias=False),
            nn.BatchNorm2d(out_channels)
        ])
        
        self.conv = nn.Sequential(*layers)
        
    def forward(self, x):
        if self.use_residual:
            return x + self.conv(x)
        return self.conv(x)

第四部分：实际应用与性能分析

4.1 MobileNet系列

Google的MobileNet系列是深度分离卷积最著名的应用：

1. MobileNetV1：首次系统性地使用深度分离卷积构建轻量化网络

2. MobileNetV2：引入倒残差结构和线性瓶颈

3. MobileNetV3：结合神经网络架构搜索(NAS)和注意力机制

4.2 EfficientNet的复合缩放

EfficientNet提出了一种复合缩放方法，统一调整网络宽度、深度和分辨率。其基础构建块MBConv就是基于深度分离卷积的倒残差结构。

4.3 性能对比

在ImageNet分类任务上，不同轻量化网络的对比：

模型	参数量(M)	FLOPs(B)	Top-1 Acc(%)
MobileNetV1	4.2	0.575	70.6
MobileNetV2	3.4	0.3	72.0
MobileNetV3-Small	2.5	0.056	67.4
EfficientNet-B0	5.3	0.39	77.1

4.4 部署优势

深度分离卷积在移动设备上的优势尤为明显：

1. 内存占用低：参数少，减少内存带宽需求

2. 计算效率高：适合移动GPU/DSP的并行计算模式

3. 能耗低：减少计算量直接降低能耗

实测数据显示，在相同精度下，基于深度分离卷积的网络比标准CNN在移动设备上快3-5倍，能耗降低2-4倍。

第五部分：局限性与未来方向

5.1 深度分离卷积的局限性

尽管深度分离卷积有很多优点，但也存在一些局限：

1. 训练难度：深度卷积的参数较少，可能导致训练不稳定

2. 特征表示能力：分离操作可能损失部分空间-通道联合信息

3. 硬件支持：某些硬件对深度分离卷积的优化不如标准卷积完善

5.2 混合结构设计

一些最新研究尝试将深度分离卷积与标准卷积结合：

• 在关键层使用标准卷积保持表示能力

• 在大部分层使用深度分离卷积减少计算量

• 动态决定哪些层应该使用分离结构

5.3 自动化设计

神经网络架构搜索(NAS)正被用于自动发现最优的深度分离卷积组合：

• 搜索每个块是否应该使用深度分离结构

• 优化扩展比例和通道数

• 联合优化网络拓扑和分离策略

5.4 新型分离范式

研究人员正在探索更复杂的分离方式：

• 频域分离

• 通道分组分离

动态分离(根据输入决定分离方式)

结语

深度分离卷积模块代表了深度学习模型设计从"越大越好"向"高效智能"转变的重要里程碑。通过解耦空间滤波和通道组合这两个功能，它实现了计算效率的质的飞跃，使高性能神经网络能够在资源受限的设备上运行。从MobileNet到EfficientNet，深度分离卷积不断演进，结合新的设计理念如倒残差、注意力机制等，持续推动着轻量化网络的发展。

未来，随着自动化机器学习技术和新型硬件架构的发展，深度分离卷积可能会进一步演化，出现更智能、更高效的变体。但无论如何发展，其核心思想——通过合理的分解减少冗余计算——将继续指导高效神经网络的设计。

对于从业者而言，理解深度分离卷积不仅有助于应用现有轻量化模型，更能启发我们设计适合特定场景的高效架构。在边缘计算和物联网时代，这种能力将变得越来越宝贵。