【第一次团体赛赛后部分题解】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
第一次团体赛赛后部分题解
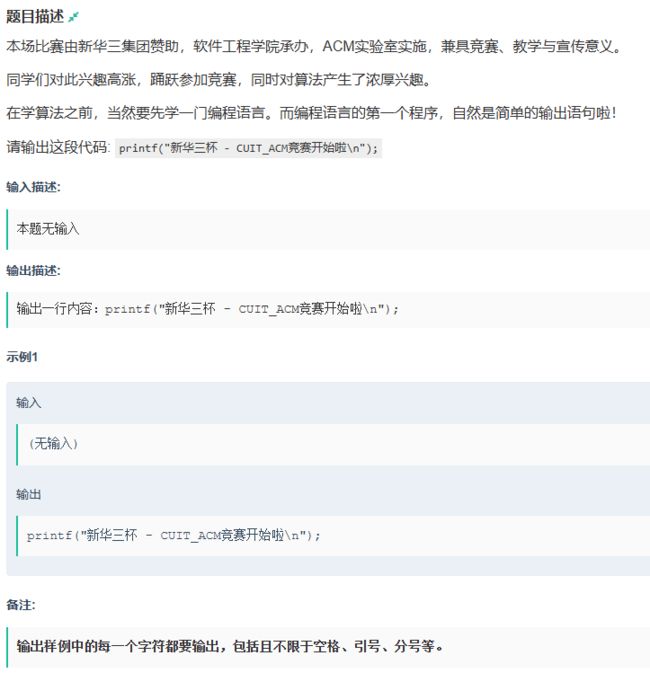
- A 欢迎来到算法世界
- B 更待西湖彻底干 此间应有再生缘
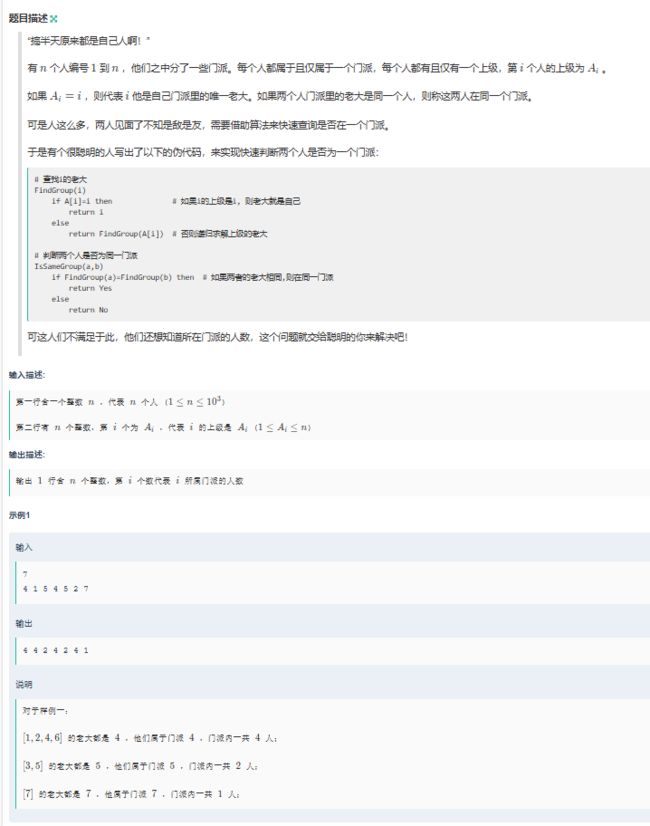
- D 我上面有人儿
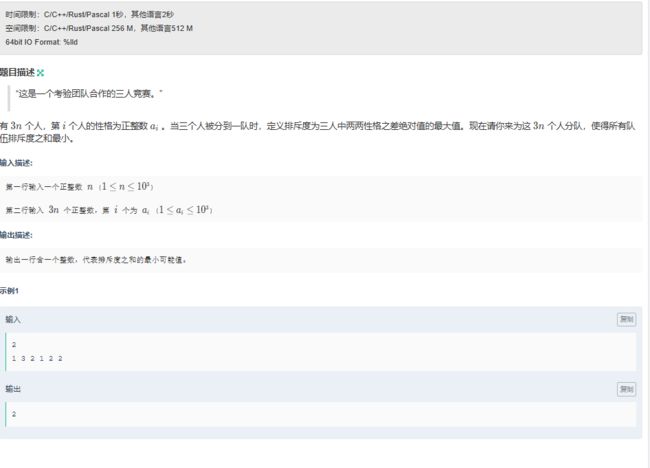
- G 三人成行
- J 娇の礼帽
- K 我来组成头部
- 总结
A 欢迎来到算法世界
#include解题思路:这道题跟以往打印题不同,以往打印题不是汉字就是英语,这次需要打印的话包含了C语言中的一些符号,比如printf,(,),\n,;等等,正常直接打印是不行的,只能把它分解成几段字符串,使它失去原本的作用,另外还考察了转义字符的应用,在 C 语言里,转义字符以反斜杠 \ 开头,用来表示一些无法直接输入的字符或者有特殊用途的字符,\n直接输出会导致换行,前边加个\会让它失去作用。
B 更待西湖彻底干 此间应有再生缘
#include解题思路:这道题很长,刚开始吓我一跳,结果只用这么短就ac了,一个人除了他自己和伴侣以外的异性拥抱,只需要拥抱n-1次,因为有n对,不带他俩就剩n-1次。
D 我上面有人儿
#include解题思路:定义一个find函数找每个人的老大,利用递归查找当前人的门派老大。若a[i]等于i,说明i就是自己门派的老大,直接返回i;否则,继续递归查找a[i]的老大,直到找到门派的最终老大。遍历每个人,通过find函数找到其门派老大b[i],并将对应老大的门派人数c[find(i)]加 1 。这样就完成了每个门派人数的统计。
G 三人成行
#include解题思路:先sort排序,排序后第一个数和第三个数的差的绝对值就是最大排斥度,用for循环,遍历每三个人的第一个人,用sum加起来每组的最大排斥度就行了。
J 娇の礼帽
#include解题思路:特殊情况分析:对于只有 1 个人的情况,由于没有任何可参考信息,猜对帽子颜色的概率是 50%,所以答对人数的期望就是0.5×1=0.5。
多人情况策略制定:当人数大于 1 时,采用如下策略。让最后一个人(第n个人)先回答,他没有足够信息确定自己帽子颜色,只能随机猜,猜对概率为 50%。但他可以通过回答传递关键信息,比如说出前n−1个人中黑色帽子数量的奇偶性。
信息传递与推断:第n−1个人听到第n个人的回答后,结合自己看到的前n−2个人的帽子颜色情况,就能推断出自己帽子的颜色。因为他知道前n−1个人黑色帽子数量的奇偶性,又看到了前n−2个人的情况,所以可以确定自己帽子颜色,从而必然答对。
依此类推:从第n−2个人到第 1 个人,都可以按照同样的方式,根据后面人传递的信息和自己看到的前面人的帽子颜色,准确推断出自己帽子的颜色,他们答对的概率都是 1。
计算期望:综合以上情况,答对人数的期望就是前面n−1个人必然答对的人数(n−1)乘以答对概率(1),再加上最后一个人答对的期望(0.5),即(n−1)×1+0.5=n−0.5。在编程实现时,先读取询问次数q,然后对每次询问读取人数n,按照n−0.5计算答对人数期望并输出
K 我来组成头部
#include
这道题是一道找规律题,由于是多实例,再加上超绝n的范围(109),说明得考虑一下o(1)的方法,也就是找规律。
总结
通过这次比赛,我发现找规律的题比较多。找到规律就可以直接做出来,找不到就over了。