【动态规划】背包问题(01背包,完全背包,多重背包,分组背包)
01背包
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 v i v_i vi, w i w_i wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
01背包问题,最基础的背包问题,每件物品只有一件,可以选择放或不放
状态转移方程为 f[i][j] = max(f[i - 1][j] , f[i - 1][j - v[i]] + w[i])
其中 f[i][j] 是前i件物品,背包容量是j的最大价值
当选择不放第i件物品时,那么问题就转化为 前i-1件物品放入容量为v的背包中 ,即f[i][j] = f[i - 1][j]
当选择放第i件物品时,那么问题就变成了 前i-1件物品放入剩下的容量为v-c[i]的背包中 ,即f[i][j] = f[i - 1][j - v[i]] + w[i]
代码如下
import java.io.*;
import java.util.*;
public class Main {
static final int N = 1010;
static int[] volume = new int[N];
static int[] value = new int[N];
static int[][] maxValue = new int[N][N];
public static void main(String[] args) throws Exception {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int v = sc.nextInt();
for(int i = 1; i <= n; i++) {
volume[i] = sc.nextInt();
value[i] = sc.nextInt();
}
//计算最大价值
for(int i = 1; i <= n; i++) {
for(int j = 0; j <= v; j++) {
maxValue[i][j] = maxValue[i - 1][j];
if(j >= volume[i]) {
maxValue[i][j] = Math.max(maxValue[i - 1][j], maxValue[i - 1][j - volume[i]] + value[i]);
}
}
}
System.out.println(maxValue[n][v]);
sc.close();
}
}
下面通过一个具体的例子模拟一下整个过程
有三个物品,编号为1、2、3,其体积和价值如下表,背包的容积是10
| 编号 | 体积 | 价值 |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 6 |
以下过程十分详细,但看起来也很恶心,如果已经理解了整个过程,可以直接看后面的一维优化
当 i = 1 (考虑物品 1)
外层循环 i 代表当前考虑的物品编号,内层循环 j 代表当前背包容量。
当 j = 0 :
maxValue[1][0] = maxValue[0][0] = 0 ,因为 j < volume[1] ,不放入物品 1。
当 j = 1 :
maxValue[1][1] = maxValue[0][1] = 0 ,因为 j < volume[1] ,不放入物品 1。
当 j = 2 :
maxValue[1][2] = maxValue[0][2] = 0 ,因为 j < volume[1] ,不放入物品 1。
当 j = 3 :
maxValue[1][3] = maxValue[0][3] = 0 ,因为 j < volume[1] ,不放入物品 1。
当 j = 4 :
maxValue[1][4] = Math.max(maxValue[0][4], maxValue[0][4 - 4] + value[1]) = Math.max(0, 0 + 5) = 5 ,可以放入物品 1。
当 j = 5 :
maxValue[1][5] = Math.max(maxValue[0][5], maxValue[0][5 - 4] + value[1]) = Math.max(0, 0 + 5) = 5 ,可以放入物品 1。
当 j = 6 :
maxValue[1][6] = Math.max(maxValue[0][6], maxValue[0][6 - 4] + value[1]) = Math.max(0, 0 + 5) = 5 ,可以放入物品 1。
当 j = 7 :
maxValue[1][7] = Math.max(maxValue[0][7], maxValue[0][7 - 4] + value[1]) = Math.max(0, 0 + 5) = 5 ,可以放入物品 1。
当 j = 8 :
maxValue[1][8] = Math.max(maxValue[0][8], maxValue[0][8 - 4] + value[1]) = Math.max(0, 0 + 5) = 5 ,可以放入物品 1。
当 j = 9 :
maxValue[1][9] = Math.max(maxValue[0][9], maxValue[0][9 - 4] + value[1]) = Math.max(0, 0 + 5) = 5 ,可以放入物品 1。
当 j = 10 :
maxValue[1][10] = Math.max(maxValue[0][10], maxValue[0][10 - 4] + value[1]) = Math.max(0, 0 + 5) = 5 ,可以放入物品 1。
此时 maxValue[1] 数组的值为 [0, 0, 0, 0, 5, 5, 5, 5, 5, 5, 5] 。
当 i = 2 (考虑物品 2)
当 j = 0 :
maxValue[2][0] = maxValue[1][0] = 0 ,因为 j < volume[2] ,不放入物品 2。
当 j = 1 :
maxValue[2][1] = maxValue[1][1] = 0 ,因为 j < volume[2] ,不放入物品 2。
当 j = 2 :
maxValue[2][2] = maxValue[1][2] = 0 ,因为 j < volume[2] ,不放入物品 2。
当 j = 3 :
maxValue[2][3] = maxValue[1][3] = 0 ,因为 j < volume[2] ,不放入物品 2。
当 j = 4 :
maxValue[2][4] = maxValue[1][4] = 5 ,因为 j < volume[2] ,不放入物品 2。
当 j = 5 :
maxValue[2][5] = maxValue[1][5] = 5 ,因为 j < volume[2] ,不放入物品 2。
当 j = 6 :
maxValue[2][6] = maxValue[1][6] = 5 ,因为 j < volume[2] ,不放入物品 2。
当 j = 7 :
maxValue[2][7] = Math.max(maxValue[1][7], maxValue[1][7 - 7] + value[2]) = Math.max(5, 0 + 9) = 9 ,可以放入物品 2。
当 j = 8 :
maxValue[2][8] = Math.max(maxValue[1][8], maxValue[1][8 - 7] + value[2]) = Math.max(5, 0 + 9) = 9 ,可以放入物品 2。
当 j = 9 :
maxValue[2][9] = Math.max(maxValue[1][9], maxValue[1][9 - 7] + value[2]) = Math.max(5, 0 + 9) = 9 ,可以放入物品 2。
当 j = 10 :
maxValue[2][10] = Math.max(maxValue[1][10], maxValue[1][10 - 7] + value[2]) = Math.max(5, 0 + 9) = 9 ,可以放入物品 2。
此时 maxValue[2] 数组的值为 [0, 0, 0, 0, 5, 5, 5, 9, 9, 9, 9] 。
当 i = 3 (考虑物品 3)
当 j = 0 :
maxValue[3][0] = maxValue[2][0] = 0 ,因为 j < volume[3] ,不放入物品 3。
当 j = 1 :
maxValue[3][1] = maxValue[2][1] = 0 ,因为 j < volume[3] ,不放入物品 3。
当 j = 2 :
maxValue[3][2] = maxValue[2][2] = 0 ,因为 j < volume[3] ,不放入物品 3。
当 j = 3 :
maxValue[3][3] = maxValue[2][3] = 0 ,因为 j < volume[3] ,不放入物品 3。
当 j = 4 :
maxValue[3][4] = maxValue[2][4] = 5 ,因为 j < volume[3] ,不放入物品 3。
当 j = 5 :
maxValue[3][5] = Math.max(maxValue[2][5], maxValue[2][5 - 5] + value[3]) = Math.max(5, 0 + 6) = 6 ,可以放入物品 3。
当 j = 6 :
maxValue[3][6] = Math.max(maxValue[2][6], maxValue[2][6 - 5] + value[3]) = Math.max(5, 0 + 6) = 6 ,可以放入物品 3。
当 j = 7 :
maxValue[3][7] = Math.max(maxValue[2][7], maxValue[2][7 - 5] + value[3]) = Math.max(9, 5 + 6) = 11 ,可以放入物品 3。
当 j = 8 :
maxValue[3][8] = Math.max(maxValue[2][8], maxValue[2][8 - 5] + value[3]) = Math.max(9, 5 + 6) = 11 ,可以放入物品 3。
当 j = 9 :
maxValue[3][9] = Math.max(maxValue[2][9], maxValue[2][9 - 5] + value[3]) = Math.max(9, 5 + 6) = 11 ,可以放入物品 3。
当 j = 10 :
maxValue[3][10] = Math.max(maxValue[2][10], maxValue[2][10 - 5] + value[3]) = Math.max(9, 5 + 6) = 11 ,可以放入物品 3。
此时 maxValue[3] 数组的值为 [0, 0, 0, 0, 5, 6, 6, 11, 11, 11, 11] 。
观察这个二维状态转移方程可以发现,maxValue[i][j] 的计算只依赖于 maxValue[i - 1][j] 和 maxValue[i - 1][j - volume[i]],也就是说,当前状态 i 只和上一个状态 i - 1 有关。因此,我们可以只使用一个一维数组 maxValue[j] 来保存状态,在每一轮更新时,直接覆盖上一轮的状态,从而将空间复杂度从 (O(nv)) 优化到 (O(v))。
优化后版本
import java.io.*;
import java.util.*;
public class Main {
static final int N = 1010;
static int[] volume = new int[N];
static int[] value = new int[N];
static int[] maxValue = new int[N];
public static void main(String[] args) throws Exception {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int v = sc.nextInt();
for(int i = 1; i <= n; i++) {
volume[i] = sc.nextInt();
value[i] = sc.nextInt();
}
//计算最大价值
for(int i = 1; i <= n; i++) {
for(int j = v; j >= volume[i]; j--) {
maxValue[j] = Math.max(maxValue[j], maxValue[j - volume[i]] + value[i]);
}
}
System.out.println(maxValue[v]);
}
}
到这肯定会有这样的疑问:为什么内层循环要从大到小枚举
因为如果从小到大枚举的话,j - volume[i] 严格小于 j ,也就是maxValue[j - volume[i]] 可能已经在这一次中被更新过了
将其复原的话会变成 maxValue[i][j] = Math.max(maxValue[i][j], maxValue[i][j - volume[i]] + value[i]);
而不是i - 1
还是按照上面的例子详细说明:
当 i = 1 时,物品 1 的重量 volume[1] = 4,价值 value[1] = 5。
如果内层循环从小到大枚举:
当 j = 4 时:
maxValue[4] = Math.max(maxValue[4], maxValue[4 - 4] + value[1]) = Math.max(0, 0 + 5) = 5
当 j = 5 时:
maxValue[5] = Math.max(maxValue[5], maxValue[5 - 4] + value[1]) = Math.max(0, 0 + 5) = 5
当 j = 8 时:
maxValue[8] = Math.max(maxValue[8], maxValue[8 - 4] + value[1]),此时 maxValue[8 - 4] 已经在 j = 4 时被更新为放入物品 1 后的状态,即 maxValue[4] = 5,所以 maxValue[8] = Math.max(0, 5 + 5) = 10。这就意味着我们在计算 maxValue[8] 时,又一次使用了物品 1,相当于物品 1 被重复放入了背包,违背了 0 - 1 背包问题每个物品只能使用一次的规则。
当 i = 1 时,物品 1 的重量 volume[1] = 4,价值 value[1] = 5。
如果内层循环从大到小枚举:
当 j = 10 时:
maxValue[10] = Math.max(maxValue[10], maxValue[10 - 4] + value[1]) = Math.max(0, 0 + 5) = 5
当 j = 9 时:
maxValue[9] = Math.max(maxValue[9], maxValue[9 - 4] + value[1]) = Math.max(0, 0 + 5) = 5
当 j = 8 时:
maxValue[8] = Math.max(maxValue[8], maxValue[8 - 4] + value[1]),此时 maxValue[8 - 4] 还没有被更新,仍然是上一轮(即没有考虑物品 1)的状态,所以 maxValue[8] = Math.max(0, 0 + 5) = 5。
通过从大到小枚举,我们保证了在计算 maxValue[j] 时,maxValue[j - volume[i]] 是上一轮(即 i - 1 )的状态,避免了同一个物品被重复使用的问题,从而正确地实现了 0 - 1 背包问题的优化。
综上所述,内层循环从大到小枚举可以避免同一个物品被重复使用的问题,保证了状态转移的正确性。
完全背包问题
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行两个整数 v i v_i vi, w i w_i wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
10
完全背包和01背包不同的点在于,完全背包的物品可以无限次使用
状态表示和01背包相同,f[i][j]表示前i件物品,背包容量是j的最大价值
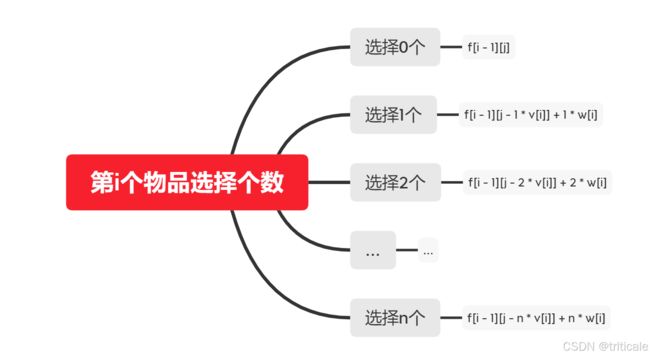
可以将第i件物品划分为选择0件,选择1一件,选择2件…选择n件(n是不得超过背包最大容量)
因此可以得出状态计算方程为 f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i])
朴素算法
import java.util.*;
public class Main {
private static final int N = 1010;
static int[] v = new int[N];
static int[] w = new int[N];
static int[][] f = new int[N][N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
for (int i = 1; i <= n; i++){
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
for(int i = 1; i <= n; i++) {
for(int j = 0; j <= m; j++) {
for(int k = 0; k * v[i] <= j; k++) {
f[i][j] = Math.max(f[i][j], f[i-1][j - k * v[i]] + k * w[i]);
}
}
}
System.out.println(f[n][m]);
}
}
观察易得
f[i][j] = max{f[i - 1][j] ,f[i - 1][j - v[i]] + w[i], f[i - 1][j - 2 * v[i]] + 2 * w[i]…}
f[i][j - v[i]] = max(f[i-1][j - v[i]] , f[i - 1][j - 2 * v[i]] + w[i] , f[i - 1][j - 3 * v[i]] + 2 * w[i] ,…)
可见f[i][j] 可以改写为max(f[i -1][j], f[i][j - v[i]] + w[i])
由此可以将三层循环改写为二层循环
import java.util.*;
public class Main {
private static final int N = 1010;
static int[] v = new int[N];
static int[] w = new int[N];
static int[][] f = new int[N][N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
for (int i = 1; i <= n; i++){
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
for(int i = 1; i <= n; i++) {
for(int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j];
if(j >= v[i]) {
f[i][j] = Math.max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
}
System.out.println(f[n][m]);
}
}
这个和01背包问题是不是很相似
01背包中用的是第i-1层,而完全背包问题用的是第i层
因此再将其优化为一维的
import java.util.*;
public class Main {
private static final int N = 1010;
static int[] v = new int[N];
static int[] w = new int[N];
static int[] f = new int[N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
for (int i = 1; i <= n; i++){
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
for(int i = 1; i <= n; i++) {
for(int j = v[i]; j <= m; j++) {
f[j] = Math.max(f[j], f[j - v[i]] + w[i]);
}
}
System.out.println(f[m]);
}
}
多重背包问题
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 s i s_i si 件,每件体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 v i v_i vi, w i w_i wi, s i s_i si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0
提示:
本题考查多重背包的二进制优化方法。
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
多重背包问题的朴素算法和完全背包问题相差不多,不过是添加了枚举的数量小于总数量的条件
import java.util.*;
public class Main {
static final int N = 110;
static int[] v = new int[N];
static int[] w = new int[N];
static int[] s = new int[N];
static int[][] f = new int[N][N];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
for(int i = 1; i<= n; i++) {
v[i] = sc.nextInt();
w[i] = sc.nextInt();
s[i] = sc.nextInt();
}
for(int i = 1; i <= n; i++) {
for(int j = 0; j <= m; j++) {
for(int k = 0; k <= s[i] && k * v[i] <= j; k++) {
f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
System.out.println(f[n][m]);
sc.close();
}
}
但是因为max值不再是无限项中取最大值
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i], f[i - 1][j - 2v[i]] + 2w[i], …, f[i - 1][j - nv[i]] + nw[i])
f[i][j - v[i]] = max(f[i - 1][j -v[i]], f[i-1][j - 2v[i]] + w[i], f[i - 1][j - 3v[i]] + 2w[i], …, f[i - 1][j - nv[i]] + (n - 1)w[i], f[i -1][j - (n+1)v[i]] + nw[i])
那么如何对多重背包进行优化
可以使用一种二进制的方法
我们将i中物品的s个分为1, 2, 4, 8, 16…的组
例如1, 2 , 4, 8可以组合出0-15的任何一个整数
于是将分组后的每个“盒子”看成是01背包问题中的每个物品
import java.util.*;
public class Main {
//这里N开的数据范围的依据:多重背包问题中的一个「箱子」相当于01背包问题中的一件「物品」,实际上我们是要将s[i]用几个箱子装进去,因此我们需要估计出多重背包问题中到底有多少个箱子。
static final int N = 2400010;
static int[] v = new int[N];
static int[] w = new int[N];
//f[]是装不同背包容积下的物品最大价值,所以用背包容积来开f[]数组
static int[] f = new int[N];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
//重新定义存储物品的编号
int cnt = 0;
for(int i = 1; i <= n; i++) {
int vi = sc.nextInt();
int wi = sc.nextInt();
int si = sc.nextInt();
//定义箱子可以放物品的初始值 第一个箱子可以放一个i号物品
int k = 1;
while(k <= si) {
cnt++;
//这个箱子可以存的i号物品总体积 箱子可以放的物品总数 * 物品体积 = 物品总体积
v[cnt] = vi * k;
w[cnt] = wi * k;
//从i号物品总个数中减去这个箱子装的k个 方便while循环条件判断
si -= k;
//二进制优化 下一个箱子可以放的物品数量是上一个的两倍
k *= 2;
}
//如果物品i还没有被二进制箱子存完 再开一个可以存还剩下的所有物品i的箱子
if(si > 0) {
cnt++;
v[cnt] = vi * si;
w[cnt] = wi * si;
}
}
//现在总数已经是cnt个了
n = cnt;
//做一遍01背包即可
for(int i = 1; i <= n; i++) {
for(int j = m; j >= v[i]; j--) {
f[j] = Math.max(f[j], f[j -v[i]] + w[i]);
}
}
System.out.println(f[m]);
sc.close();
}
}
分组背包问题
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 v i j v_{ij} vij,价值是 w i j w_{ij} wij,其中 i 是组号,j 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有 N 组数据:
- 每组数据第一行有一个整数 S i S_i Si,表示第 i 个物品组的物品数量;
- 每组数据接下来有 S i S_i Si 行,每行有两个整 v i j v_{ij} vij, w i j w_{ij} wij,用空格隔开,分别表示第 i 个物品组的第 j 个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
数据范围
0
0< v i j v_{ij} vij, w i j w_{ij} wij≤100
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例:
8
分组背包问题状态表示
f[i][j] 为前i组物品中体积为j的最大价值
状态计算f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i][k]] + w[i][k])
import java.io.*;
import java.util.*;
public class Main {
static final int N = 110;
static int[][] v = new int[N][N];
static int[][] w = new int[N][N];
static int[] groupSize = new int[N];
static int[] f = new int[N];
public static void main(String[] agrs) throws Exception {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
for(int i = 1; i <= n; i++) {
groupSize[i] = sc.nextInt();
for(int j = 1; j <= groupSize[i]; j++) {
v[i][j] = sc.nextInt();
w[i][j] = sc.nextInt();
}
}
//枚举每一组
for(int i = 1; i <= n; i++) {
//枚举体积,从大到小
for(int j = m; j >= 0; j--) {
//枚举每个物品
for(int k = 1; k <= groupSize[i]; k++) {
if(j >= v[i][k]) {
f[j] = Math.max(f[j], f[j - v[i][k]] + w[i][k]);
}
}
}
}
System.out.println(f[m]);
sc.close();
}
}