poj 3083 DFS 和BFS

Children of the Candy Corn

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 6630		Accepted: 2891

Description

The cornfield maze is a popular Halloween treat. Visitors are shown the entrance and must wander through the maze facing zombies, chainsaw-wielding psychopaths, hippies, and other terrors on their quest to find the exit. 

One popular maze-walking strategy guarantees that the visitor will eventually find the exit. Simply choose either the right or left wall, and follow it. Of course, there's no guarantee which strategy (left or right) will be better, and the path taken is seldom the most efficient. (It also doesn't work on mazes with exits that are not on the edge; those types of mazes are not represented in this problem.) 

As the proprieter of a cornfield that is about to be converted into a maze, you'd like to have a computer program that can determine the left and right-hand paths along with the shortest path so that you can figure out which layout has the best chance of confounding visitors.

Input

Input to this problem will begin with a line containing a single integer n indicating the number of mazes. Each maze will consist of one line with a width, w, and height, h (3 <= w, h <= 40), followed by h lines of w characters each that represent the maze layout. Walls are represented by hash marks ('#'), empty space by periods ('.'), the start by an 'S' and the exit by an 'E'. 

Exactly one 'S' and one 'E' will be present in the maze, and they will always be located along one of the maze edges and never in a corner. The maze will be fully enclosed by walls ('#'), with the only openings being the 'S' and 'E'. The 'S' and 'E' will also be separated by at least one wall ('#'). 

You may assume that the maze exit is always reachable from the start point.

Output

For each maze in the input, output on a single line the number of (not necessarily unique) squares that a person would visit (including the 'S' and 'E') for (in order) the left, right, and shortest paths, separated by a single space each. Movement from one square to another is only allowed in the horizontal or vertical direction; movement along the diagonals is not allowed.

Sample Input

2

8 8

########

#......#

#.####.#

#.####.#

#.####.#

#.####.#

#...#..#

#S#E####

9 5

#########

#.#.#.#.#

S.......E

#.#.#.#.#

#########

Sample Output

37 5 5

17 17 9

---

转自：http://www.cnblogs.com/lyy289065406/archive/2011/07/31/2122369.html

题目大意:

给定一个迷宫，S是起点，E是终点，#是墙不可走，.可以走

先输出左转优先时，从S到E的步数

再输出右转优先时，从S到E的步数

最后输出S到E的最短步数

 

 

W为宽，列数

H为高，行数

 

 

 

解题思路：

DFS和BFS的综合题水题，难度不大，但是写代码时要注意几方面：

 

1、 左转、右转优先搜索时必须标记当前位置时的方向，我定义的方向是

    

 

 

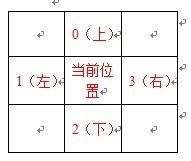
最初的方向由起点S确定，而下一步的方向则由前一步的走向决定

 

例如 左边优先搜索：

当前位置的方向指向 1（向左），(这同时说明前一步是在第“3”的位置走过来的)

那么走下一步时，就要根据2103的顺序，先逐格确定当前位置周边的四格是否可行

若第一次确认2可行，就走到2，在位置2时的方向为2（向下）

若2不可行，则再确定1，若1可行，就走到1，在位置1时的方向为1（向左）

  若1也不可行，则再确定0，若0可行，就走到0，在位置0时的方向为0（向上）

  若0也不可行，说明进入了迷宫的死胡同，要从原路返回，走回3

 

右边优先搜索也同理。

 

根据我定义的方向，设当前位置为d，那么

左转，用数学式子表达就是  d=(d+1)%4

右转，用数学式子表达就是  d=(d+3)%4

我比较懒，在我的程序中，DFS和BFS都用了多入口的做法，有兴趣的同学可以利用我给出的这两个式子对代码进行优化。

        

这里有一点必须要注意的：

左边、右边优先搜索都不是找最短路，因此走过的路可以再走，无需标记走过的格

 

2、 寻找最短路只能用BFS

因此在做第3问时别傻乎乎的又用DFS，DFS对于样例的输入确实和BFS得到的结果一样的，别以为样例PASS就提交了。。。所以我就说样例没代表性，学会测试数据很重要= =

 

注意有一点：

要求E的最短路，必须把迷宫模拟为树，S为根，找到E所在的层（树深），该层就是S到E的最短路，处理技巧就是在BFS时，令queue[tail]的depth等于对应的queue[head]的depth+1，详细见我的程序

把循环的次数作为深度就铁定错的

---

代码：

View Code

  1 #include <iostream>

  2 #include <stdio.h>

  3 #include <string.h>

  4 using namespace std;

  5 

  6 struct M{

  7     int r,c;

  8     int depth;    

  9 };

 10 

 11 M s,e;

 12 int Lstep,Rstep;    //左/右优先的步数

 13 

 14 bool maze[41][41];

 15 

 16 void DFS_L(int i,int j,int d)   //左边优先搜索， i,j是当前坐标，d为位置方向

 17 {

 18     Lstep++;

 19     if(i==e.r && j==e.c)

 20     {

 21         return ;

 22     }

 23     switch(d)                    //由图可以看出

 24     {

 25         case 0:

 26             {

 27                 if(maze[i][j-1])

 28                     DFS_L(i,j-1,1);

 29                 else if(maze[i-1][j])

 30                     DFS_L(i-1,j,0);

 31                 else if(maze[i][j+1])

 32                     DFS_L(i,j+1,3);

 33                 else if(maze[i+1][j])

 34                     DFS_L(i+1,j,2);

 35                 break;

 36             }

 37         case 1:

 38             {

 39                 if(maze[i+1][j])

 40                     DFS_L(i+1,j,2);

 41                 else if(maze[i][j-1])

 42                     DFS_L(i,j-1,1);

 43                 else if(maze[i-1][j])

 44                     DFS_L(i-1,j,0);

 45                 else if(maze[i][j+1])

 46                     DFS_L(i,j+1,3);

 47                 break;

 48             }

 49         case 2:

 50             {

 51                 if(maze[i][j+1])

 52                     DFS_L(i,j+1,3);

 53                 else if(maze[i+1][j])

 54                     DFS_L(i+1,j,2);

 55                 else if(maze[i][j-1])

 56                     DFS_L(i,j-1,1);

 57                 else if(maze[i-1][j])

 58                     DFS_L(i-1,j,0);

 59                 break;

 60             }

 61         case 3:

 62             {

 63                 if(maze[i-1][j])

 64                     DFS_L(i-1,j,0);

 65                 else if(maze[i][j+1])

 66                     DFS_L(i,j+1,3);

 67                 else if(maze[i+1][j])

 68                     DFS_L(i+1,j,2);

 69                 else if(maze[i][j-1])

 70                     DFS_L(i,j-1,1);

 71                 break;

 72             }

 73     }

 74     return ;

 75 }

 76 

 77 void DFS_R(int i,int j,int d)

 78 {

 79     Rstep++;

 80     if(i==e.r && j==e.c)

 81         return;

 82     switch(d)

 83     {

 84         case 0:

 85             {

 86                 if(maze[i][j+1])

 87                     DFS_R(i,j+1,3);

 88                 else if(maze[i-1][j])

 89                     DFS_R(i-1,j,0);

 90                 else if(maze[i][j-1])

 91                     DFS_R(i,j-1,1);

 92                 else if(maze[i+1][j])

 93                     DFS_R(i+1,j,2);

 94                 break;

 95             }

 96         case 1:

 97             {

 98                 if(maze[i-1][j])

 99                     DFS_R(i-1,j,0);

100                 else if(maze[i][j-1])

101                     DFS_R(i,j-1,1);

102                 else if(maze[i+1][j])

103                     DFS_R(i+1,j,2);

104                 else if(maze[i][j+1])

105                     DFS_R(i,j+1,3);

106                 break;

107             }

108         case 2:

109             {

110                 if(maze[i][j-1])

111                     DFS_R(i,j-1,1);

112                 else if(maze[i+1][j])

113                     DFS_R(i+1,j,2);

114                 else if(maze[i][j+1])

115                     DFS_R(i,j+1,3);

116                 else if(maze[i-1][j])

117                     DFS_R(i-1,j,0);

118                 break;

119             }

120         case 3:

121             {

122                 if(maze[i+1][j])

123                     DFS_R(i+1,j,2);

124                 else if(maze[i][j+1])

125                     DFS_R(i,j+1,3);

126                 else if(maze[i-1][j])

127                     DFS_R(i-1,j,0);

128                 else if(maze[i][j-1])

129                     DFS_R(i,j-1,1);

130                 break;

131             }

132     }

133     return;

134 }

135 

136 void BFS(int i, int j)                    //    i,j为起始位置

137 {

138     bool vis[41][41]={false};

139     M queue[1605];

140     int head,tail;

141     head=tail=0;

142     queue[0].r=i;

143     queue[0].c=j;

144     queue[tail++].depth=1;

145     vis[i][j]=true;

146 

147     while(head<tail)

148     {

149         M x=queue[head++];

150         if(x.r==e.r && x.c==e.c)

151         {

152             printf("%d\n",x.depth);

153             return;

154         }

155         if(maze[x.r][x.c-1] && !vis[x.r][x.c-1])

156         {

157             vis[x.r][x.c-1]=true;

158             queue[tail].r=x.r;

159             queue[tail].c=x.c-1;

160             queue[tail++].depth=x.depth+1;

161         }

162         if(maze[x.r-1][x.c] && !vis[x.r-1][x.c])

163         {

164             vis[x.r-1][x.c]=true;

165             queue[tail].r=x.r-1;

166             queue[tail].c=x.c;

167             queue[tail++].depth=x.depth+1;

168         }

169         if(maze[x.r][x.c+1] && !vis[x.r][x.c+1])

170         {

171             vis[x.r][x.c+1]=true;

172             queue[tail].r=x.r;

173             queue[tail].c=x.c+1;

174             queue[tail++].depth=x.depth+1;

175         }

176         if(maze[x.r+1][x.c] && !vis[x.r+1][x.c])

177         {

178             vis[x.r+1][x.c]=true;

179             queue[tail].r=x.r+1;

180             queue[tail].c=x.c;

181             queue[tail++].depth=x.depth+1;

182         }

183 

184     }

185     return;

186 }

187 

188 int main()

189 {

190     int t;

191     int i,j;

192     scanf("%d",&t);

193     while(t--)

194     {

195         int dir;

196         int w,h;

197         scanf("%d%d",&w,&h);

198         Lstep=1;

199         Rstep=1;

200         memset(maze,false,sizeof(maze));

201 

202         for(i=1;i<=h;i++)

203         {

204             for(j=1;j<=w;j++)

205             {

206                 char tt;

207                 cin>>tt;

208                 if(tt=='.')

209                     maze[i][j]=true;

210                 if(tt=='S')

211                 {

212                     maze[i][j]=true;

213                     s.r=i;

214                     s.c=j;

215                     if(i==h) dir=0;                //判断其实dir方向

216                     else if(j==w) dir=1;        

217                     else if(i==1) dir=2;

218                     else if(j=1) dir=3;

219                 }

220                 if(tt=='E')

221                 {

222                     maze[i][j]=true;

223                     e.r=i;

224                     e.c=j;

225                 }

226 

227             }

228         }

229         switch(dir)

230         {

231             case 0: {DFS_L(s.r-1,s.c,0);break;}                //    题目描述，所有S两边都是'#'。

232             case 1: {DFS_L(s.r,s.c-1,1);break;}

233             case 2: {DFS_L(s.r+1,s.c,2);break;}

234             case 3: {DFS_L(s.r,s.c+1,3);break;}

235         }

236         cout<<Lstep<<' ';

237 

238         switch(dir)

239         {

240             case 0: {DFS_R(s.r-1,s.c,0);break;}

241             case 1: {DFS_R(s.r,s.c-1,1);break;}

242             case 2: {DFS_R(s.r+1,s.c,2);break;}

243             case 3: {DFS_R(s.r,s.c+1,3);break;}

244         }

245         cout<<Rstep<<' ';

246         

247         BFS(s.r,s.c);

248     }

249     return 0;

250 }