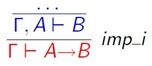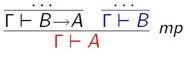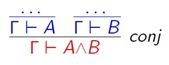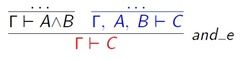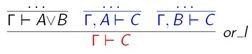coq 的一点体会
用coq做了一个作业,所以现在会一点点证明了。不过这只是coq中的很小很小的一部分,现在把我的理解写出来。
首先隆重介绍命题逻辑的5种基本连接词:
- ~ 非
- /\ 合取
- \/ 析取
- -> 蕴含
- <-> 等价
每种连接都有两种基本规则:
- introduction rule 引入规则
- elimination rule 删除规则
这些规则是用来证明一个命题是否正确的根本。下面来分别介绍之,因为我的学术水平十分一般,所以接下来打算用最通俗的语言来解释~
1. 蕴含的引入规则 intros H
这么看是挺抽象的,这是一种表达方式。A和B都是公式,上面是前提,下面是结论。这个规则的意思就是,如果┏和A都成立推出B成立,那么┏成立可以推出A->B。
(大概是这么个意思,可能某些术语不对,毕竟学数理逻辑是三年前的事情了= =)。。
在coq中,是根据结果来一步步往上推,然后用前提条件将其消去。也就是说,coq中使用引入规则是将横线下的部分转换成横线上的部分来证明。
比如说当前状态是要证B。coq的显示为:
……
=================
A->B
我输入coq> intros H.
将获得一个前提A。
……
H :A
=================
B
2. 蕴含的删除规则 apply H
这个我就不解释了。。反正就是上面前提下面结论,coq里面倒着用。比如说我有一个前提H:B->A,可以用它来把要证的结论A替换成B。
输入coq>apply H.
下面来个综合示例。从PPT里偷来的。
coq输入:
Section Propositional_Logic.
Variables P Q R : Prop.
Lemma imp_dist : (P ->(Q -> R)) -> (P -> Q) -> P -> R.
Proof.
显示如下:
1 subgoal
P : Prop
Q : Prop
R : Prop
============================
(P –> Q –> R) –> (P –> Q) –> P –> R
输入coq>intros H H0 p.
显示如下,可以看到式子被分解了:
1 subgoal:
P : Prop
Q : Prop
R : Prop
H : P –>Q –> R
H0 : P –> Q
p : P
============================
R
输入coq>apply H.
显示如下:
2 subgoals:
P : Prop
Q : Prop
R : Prop
H : P -> Q -> R
H0 : P -> Q
p : P
============================
P
subgoal 2 is:
Q
coq>assumption.
这里解释一下,assumption表示要使用前提中为真的命题,p:P表示P已经为真了,我们可以直接拿来用。
然后显示如下:
1 subgoal:
P : Prop
Q : Prop
R : Prop
T : Prop
H : P -> Q -> R
H0 : P -> Q
p : P
============================
Q
继续输入:
coq>apply H0;assumption.
Proof completed
coq>Qed.
这样就算证完了一个命题了。
3. 等价的拆分 split
<->在数理逻辑里都是拆成两部分证明的,先证A->B再证B->A这样。在coq遇到这样的问题也是先拆,要拆结论的话命令是split。因为示例太占空间了,我这里就不显示了。
对于前提中的命题H : A<->B,拆分的方法是destruct H as [H1 H2],这样就可以看到自己获得了两个前提H1 : A->B H2 : B->A。
这样的方法同样适用于A /\ B,接下来也会介绍。
4. 合取的引入规则 split
在coq中用这个命令就是将结论拆成两个分开来证明,因为coq是倒着证的。输入了coq>split.后,显示中的目标会变成2个,A和B都要证。
5. 合取的删除规则 destruct
使用destruct指令可以将前提拆分。假设H :A /\ B。那么输入coq>destruct H as [H1 H2]将生成两个新的前提:H1 : A 和 H2 : B。
下面举个例子:
Lemma and_comm : P /\ Q –> Q /\ P.
Proof.
intro H.
1 subgoal
P : Prop
Q : Prop
H : P /\ Q
============================
Q /\ P
destruct H as [H1 H2].
1 subgoal
P : Prop
Q : Prop
H1 : P
H2 : Q
============================
Q /\ P
split.
2 subgoals
P : Prop
Q : Prop
H1 : P
H2 : Q
============================
Q
subgoal 2 is:
P
...
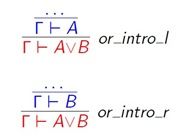
6. 析取的引入规则 left & right
对目标结论输入coq>left.能够使目标变为A,同理right变成B。选择其中一个你觉得证起来比较简单的子式吧~
7. 析取的删除规则 destruct
如果有前提H : A \/ B,输入coq>destruct H as [H1|H2]将它拆分成两个前提。这个跟前面类似,只是用的是或连接符“|”,就不多说了。
8. 非的引入规则 intros H
非的引入规则是intros H。假设结果是~A。输入coq> intros H.将得到H : A,此时要证的结论是False。
9. 非的删除规则 elim H
非的删除规则用于将目标False替换为A,假如有前提H : ~A的话,反之亦然,只要输入coq>elim H.就行了。接下来就可以证明A了。
命题逻辑我知道的基本就这么多,关于谓词逻辑的,且听下回分解。>_<
本文原创,转载请注明出处: