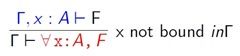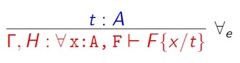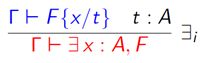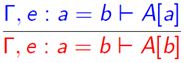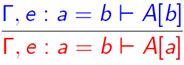coq的一点体会2
下面是谓词逻辑。在coq里,量词的表示如下:
全称量词:forall
存在量词:exists
同样都有自己的引入规则和删除规则
1. forall引入规则 intros x
输入intros x就可以提取出一个前提x,使得结论成为F。intros前面有讲很多,这里就不多说了。
2. forall删除规则 apply H
对于已知的前提H : forall x:A , F.可以用它来简化结论,比如对于H : forall x:A, P x -> forall y:A, R x y -> R x (f y),输入coq>apply H. 可以看到目标R a (f (f a))被分解为两个:P a 和 R a (f a)
下面来举个课件中的例子。。下面有用到";" 意思就是两句合并到一起执行。注意有时A ; B与A. (换行) B. 的运行结果是不一样的,这两句并不等价。
输入:
Hypothesis Hf : forall x y:A, R x y -> R x (f y).
Hypothesis R_refl : forall x:A, R x x.
Lemma Lf : forall x :A, R x (f (f (f x))).
Proof.
intro x;apply Hf.
1 subgoal
Hf : forall x y : A, R x y -> R x (f y)
R refl : forall x : A, R x x
x : A
============================
R x (f (f x))
repeat apply Hf.
1 subgoal
A : Set
f : A -> A
Hf : forall x y : A, R x y -> R x (f y)
R refl : forall x : A, R x x
x : A
============================
R x x
apply R_refl.
Qed.
有时候应用前提来证明时,系统并不知道如何给forall x:A找到一个合适的赋值,在我们输入apply H时,会给出如下的错误提示:
Error: Unable to find an instance for the variable m.
这时需要给出H的赋值,使用with后缀。下面看一个例子:
Hypothesis lt_trans : forall n m p : nat, n < m -> m < p -> n < p.
Lemma lt_n_SSn : forall i:nat, i < S (S i).
Proof.
intro i.
1 subgoal
Hypothesis lt_trans : forall n m p : nat, n < m -> m < p -> n < p
i : nat
===========================
i < S (S i)
如果这时输入的是apply lt_trans. 会给出错误提示找不到m的实例。正确的输入应该是:
apply lt_trans with (S i);
目标这时就会分解为 i < S i 和 S i < S (S i)。类似的可以输入eapply lt_trans. 系统会自动找一个随机变量替代m。
注:with x 这一后缀同样适用于elim子句。
3. 存在量词引入规则 exists t
输入exists t. 提取出F来证明。需要注意的是这个t必须是在前提中存在的。
4. 存在量词删除规则 destruct H as [x Hx]
输入destruct H as [x Hx]. ,将前提H分解为两个,分别是x和Hx :F –> G。
5. 等价性引入规则 reflexivity
当证明目标是很显然的a=a时,可以输入reflexivity, trivial, auto中的一个来证明。
6. 替换规则
已知前提e : a=b,想要用b来替换目标A[a]中的a,可以输入rewrite –>e.
同样的
用a来替换b:rewrite <-e.
还是比较直观的,下面是一个例子:
Lemma eq_trans_on_A :
forall x y z:A, x = y -> y = z -> x = z.
Proof.
intros x y z e.
. . .
e : x = y
============================
y = z -> x = z
rewrite -> e.
. . .
e : x = y
============================
y = z -> y = z
class over~
本文原创,转载请注明出处: