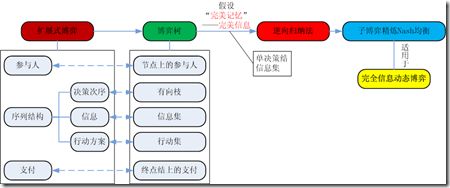
博弈论——扩展式博弈
图1 扩展式博弈
1. 问题提出——新产品开发
两企业(企业1和企业2)准备各自开发同一新产品,并投放市场。开发中企业的投入、产出如图所示:
图2 新产品开发投入-产出图
两个企业都知道市场需求,且企业1先决策,企业2观测到企业1的选择后再进行选择。试问企业1和企业2将如何选择?
2. 问题描述——扩展式博弈
扩展式博弈(extensive form game):与战略式博弈侧重博弈结果相比,扩展式博弈更注重对参与人在博弈过程中所遇到决策问题的序列结构的详细分析。
描述方式:博弈树
扩展式博弈四要素:
2) 参与人的行动顺序;
3) 每个参与人行动时面临的决策问题,包括参与人行动时可供他选择的行动方案及他所了解的信息;
4) 参与人的支付函数
“新产品开发”博弈扩展式描述:
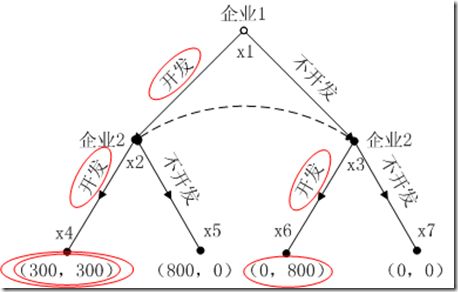
图3 需求大的情况下新产品开发博弈的博弈树描述
图4 需求小的情况下新产品开发博弈的博弈树描述
3. 问题的解——子博弈精炼Nash均衡
子博弈:原博弈的一部分,始于原博弈中一个位于单结信息集中的决策结x,并由决策结x及其后续结共同组成,与原博弈具有相同的信息结构。
扩展式博弈的战略组合![]() 是一个子博弈精炼Nash均衡,当且仅当满足以下条件:
是一个子博弈精炼Nash均衡,当且仅当满足以下条件:
1) 它是原博弈的Nash均衡;
2) 它在每个子博弈上给出(或构成)Nash均衡。
逆向归纳法:
1) 找出博弈的所有子博弈
2) 按照博弈进程的“反方向”逐一求解各个子博弈,即最先求解最底层的子博弈,在求解上一层的子博弈,……,直至原博弈。
图5 逆向归纳法求解新产品开发博弈(需求大)
子博弈精炼Nash均衡为(开发,(开发,开发))
图6 逆向归纳法求解新产品开发博弈(需求小)
子博弈精炼Nash均衡(开发,(不开发,开发))
Kuhn定理:每个有限的扩展式博弈都存在子博弈精炼Nash均衡。
参考文献:
[1] 罗云峰. 博弈论教程. 北京: 清华大学出版社, 北京交通大学出版社, 2007.