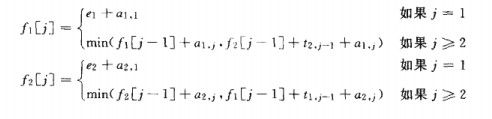数据结构 练习 16-动态规划

参考文献 《算法导论》 第15章

 

所谓“动态规划“”，就是寻求最优解的过程，采用的也是递归的思想，不过与分而治之的区别是：分治法，每个子问题是独立的，只要求出每个字问题，然后合并一下，就可以了；而动态规划虽然也是递归的过程，但子问题不独立，下文将结合例子讲解。

根据《算法导论》，动态规划(dynamic programming) 包括一下四个方面：

1，描述最优解的结构

2，递归定义最优解的值

3，自底向上的方式计算最优解的值

4，有计算出的结果构造一个最优解。

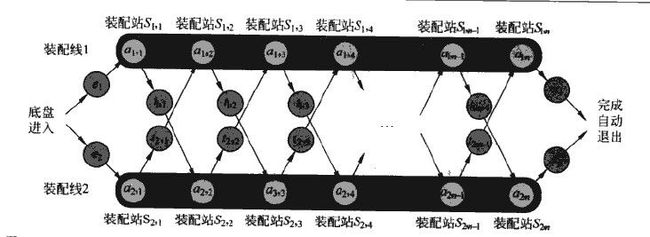
还是引用书上的装配调度来分析。不清楚题目的，请看原始第二版 P192

为了 找到最优路径，如果我们采用笨办法就是所有路径都算一遍，当然肯定可以的，但是复杂度为O(2^n)，计算机没法接受。

在此背景下，动态规划来了。

动态规划的核心思想是：子问题最优，子子问题最优，不断最优。而在最优的过程中，充分利用了，子问题之间的关系，避免重复计算。后一个最优一定是在前一个最优的基础上建立的，而分治没有。根本原因，在于，动态规划针对的就是最优问题。当然分治法也可以针对最优，但是动态规划在求最优方面是分治的进化，是更高级的东西。

据上面的例子：

假如分治法找到到a1,3的最短路径，OK,所有遍历：

e1    a1,1   a1,2    a1,3 

e 1   a1,1    a2,2   a1,3

e2    a2,1   a2,2    a1,3

e2    a2,1   a1,2    a1,3

假设采用动态规划：

通向a1,3有俩条路径，a1,2 和 a2,2

此时，分别计算通往a1,2  a2,2  的最优路径，然后比较，再决定哪条路径最优。

在此过程中，a1,2 到 a1,3只计算一次，而在，分治法中，a1,2 到a1,3计算了俩次，如上第一行和第四行，依此原理其他路径也只要计算一次；这样计算量大大缩减，当然有的人会说，每个点增加了一次比较(选择子最优)。

但是点到点之间的重复计算随着规模的增大而增大。也正由于比较的存在，一个点一次，导致最后的复杂度为O(N)。

根据《算法导论》给出递推关系式：

下面尝试给出代码：

 我自己用递归函数写的代码

#include<iostream>
using namespace std;

//声明几个全局变量。一般不建议声明全局变量，但这只是功能测试。
int a1[6]={7,9,3,4,8,4};
int a2[6]={8,5,6,4,5,7};
int t1[5]={2,3,1,3,4};
int t2[5]={2,1,2,2,1};
int e1=2;//进入站点的时间
int e2=4;
int x1=3;//退出站点的时间
int x2=2;
int l1[5];
int l2[5];//记录留个位置 
int sum1;
int sum2;
//f1 路线1上到站点_a1的最优路径的时间总和，_t1路径转移数组的下标，其余类似
void fastWay(int f1,int f2,int _t1,int _a1,int _t2,int _a2)
{  
	if(_t1>=5||_t2>=5|| _a1>=6|| _a2>=6) return;//遍历完成
	int tmp1;
	int tmp2;

	tmp1=f2+t2[_t2]+a1[_a1];
	tmp2=f1+a1[_a1];

	int inputData1,inputData2;
    if(tmp1>tmp2)
	{
        l1[_a1-1]=1;
		inputData1=tmp2;       
	}
	else
	{
        l1[_a1-1]=2;
		inputData1=tmp1;

	}

	sum1=inputData1;
	tmp1=f1+t1[_t1]+a2[_a2];
	tmp2=f2+a2[_a2];

	if(tmp1>tmp2)
	{
		l2[_a2-1]=2;
		inputData2=tmp2;
	}
	else
	{
		l2[_a2-1]=1;
		inputData2=tmp1;
	}
	sum2=inputData2;

	_t1++;
	_a1++;
	_t2++;
	_a2++;

	fastWay(inputData1,inputData2,_t1,_a1,_t2,_a2);
	
}

int main()
{
 int addedF1=e1+a1[0];
 int addedF2=e2+a2[0];
 fastWay(addedF1,addedF2,0,1,0,1);

 for(int i=0;i<5;++i)
 cout<<l1[i];
 cout<<endl;

 for(int i=0;i<5;++i)
 cout<<l2[i];
 
 if(sum1+x1>sum2+x2)
    {	
		cout<<"花的最少时间是："<<sum2+x2<<"经过的站点为：";
        for(int i=0;i<5;++i)
        cout<<l2[i];
		cout<<2;
    } 
 else
   {	
	 cout<<"花的最少时间是："<<sum1+x1<<"经过的站点为：";
      for(int i=0;i<5;++i)
        cout<<l1[i];
		cout<<1;
   }
    
return 0;
}

测试结果：

程序利用了函数的递归，需要反复压入栈，效率，不如直接循环高，如  http://www.cnblogs.com/Anker/archive/2013/03/09/2951785.html 写的代码 还是不错的。