- COCO 格式的数据集转化为 YOLO 格式的数据集
QYQY77
YOLOpython
"""--json_path输入的json文件路径--save_path保存的文件夹名字,默认为当前目录下的labels。"""importosimportjsonfromtqdmimporttqdmimportargparseparser=argparse.ArgumentParser()parser.add_argument('--json_path',default='./instances
- 处理标签包裹的字符串,并取出前250字符
周bro
前端javascript开发语言
//假设这是你的HTML字符串varhtmlString=`这是一个段落。这是一个标题这是另一个段落,包含一些链接。`;//解析HTML字符串并提取文本functionextractTextFromHTML(html){varparser=newDOMParser();vardoc=parser.parseFromString(html,"text/html");vartextContent=do
- 【Python爬虫】百度百科词条内容
PokiFighting
数据处理python爬虫开发语言
词条内容我这里随便选取了一个链接,用的是FBI的词条importurllib.requestimporturllib.parsefromlxmlimportetreedefquery(url):headers={'user-agent':'Mozilla/5.0(WindowsNT6.1;Win64;x64)AppleWebKit/537.36(KHTML,likeGecko)Chrome/80.
- 报错 | pydantic.v1.error_wrappers.ValidationError ... subclass of BaseModel expected
程序猿林仔
报错pythonpythonlangchain
文章目录01问题情景02分析问题03阅读源码04解决方案4.1方案1-指定版本安装4.2(通用)方案2-指定v1版本4.3(推荐)方案3-参考源码01问题情景最近在做Langchain的开发,可能是因为我更新了依赖库的版本,在执行下面这部分代码的时候出现了该异常:#出现该异常的代码(仅保留核心逻辑)fromlangchain.output_parsersimportPydanticOutputPa
- Java:日期类2
昭关969
java开发语言
SimpleDateFormat日期格式化类构造SimpleDateFormat(Stringpattern);pattern是我们自己制定的日期格式,字母不能改变,但连接符可以改变yyyy--MM--dd--HH时间单位字母表示Y年M月d日H时m分s秒方法Stringformat(Datedate)将Date对象按照对应格式转成StringDateparse(Stringsource)将符合我们
- 前端技能树,面试复习第 29 天—— 简述 Babel 的原理 | Webpack 构建流程 | Webpack 热更新原理 | Git 常用命令
编程轨迹_
前端面试复习笔记前端面试面经前端工程化WebpackBabel前端面试大厂面试题
31b3479814f74acbb70b9f63f2e80012.gif"width=“100%”>⭐️本文首发自前端修罗场(点击加入社区,参与学习打卡,获取奖励),是一个由资深开发者独立运行的专业技术社区,我专注Web技术、答疑解惑、面试辅导以及职业发展。。1.Babel的原理是什么?babel的转译过程也分为三个阶段,这三步具体是:解析、转换、生成解析Parse:将代码解析⽣成抽象语法树(AS
- SRT3D: A Sparse Region-Based 3D Object Tracking Approach for the Real World
Terry Cao 漕河泾
3d人工智能计算机视觉目标跟踪
基于区域的方法在基于模型的单目3D跟踪无纹理物体的复杂场景中变得越来越流行。然而,尽管它们能够实现最先进的结果,大多数方法的计算开销很大,需要大量资源来实时运行。在下文中,我们基于之前的工作,开发了SRT3D,这是一种稀疏的基于区域的3D物体跟踪方法,旨在弥合效率上的差距。我们的方法在所谓的对应线(这些线模型化了物体轮廓位置的概率)上稀疏地考虑图像信息。由此,我们改进了当前的技术,并引入了考虑定义
- 把html字符串转为可以被js操作的dom
微特尔普拉斯
javascriptwebnodejavascripthtml前端
在JavaScript中,您可以使用DOMParserAPI将HTML字符串转换为可操作的DOM节点。以下是具体步骤:1.创建DOMParser实例:constparser=newDOMParser();2.使用parseFromString()方法解析HTML字符串:consthtmlString='Hello,world!';constdoc=parser.parseFromString(ht
- Cuda 程序编译报错: fatal error: cusparse.h: No such file or directory
原野寻踪
实践经验cuda
编译cuda程序时发现下列报错:/mnt/xxx/miniconda3/envs/xxx/lib/python3.8/site-packages/torch/include/ATen/cuda/CUDAContext.h:6:10:fatalerror:cusparse.h:Nosuchfileordirectory#include^~~~~~~~~~~~检查发现是选择了错误的Cuda版本。ls/
- R语言 基础笔记
waterHBO
r语言笔记开发语言
起因:今天不知道要写什么。把之前的笔记复制一下。代码开头,导入:#清除系统变量rm(list=ls())#隐藏警告信息:options(warn=-1)#把当前目录,设置为工作目录。library(rstudioapi)current_folder_path0.0&ideology<10.0)分组聚合,类似groupby()df2<-aggregate(df1KaTeXparseerror:Exp
- Java中字符串和日期类型的相互转换
Aries263
javajvm开发语言
当在Java中进行字符串和日期类型之间的相互转换时,可以使用SimpleDateFormat类来实现。下面是一个详细的代码示例,展示了如何将字符串转换为日期类型,以及如何将日期类型转换为字符串。首先,我们来看字符串转换为日期类型的示例代码:importjava.text.ParseException;importjava.text.SimpleDateFormat;importjava.util.
- 从底层原理上理解ClickHouse 中的稀疏索引
goTsHgo
大数据分布式Clickhouse数据库clickhouse
稀疏索引(SparseIndexes)是ClickHouse中一个重要的加速查询机制。与传统数据库使用的B-Tree或哈希索引不同,ClickHouse的稀疏索引并不是为每一行数据构建索引,而是为数据存储的块或部分数据生成索引。这种索引的核心思想是通过减少需要扫描的数据范围来加速查询,特别适用于大数据量场景。1.基本概念:数据存储与索引在理解稀疏索引之前,首先需要理解ClickHouse的列式存储
- 使用爬虫写一个简易的翻译器+图像界面+python
w²大大
python学习pythontkinterjson
翻译器+图像界面+python1.效果图如下:2.代码实现1.效果图如下:2.代码实现importtkinterimportrandomimportrequestsimportrequestimporturllibfromurllibimportrequest,parseimporttime,json,random,hashlibwin=tkinter.Tk()defpachong():try:u
- 配置QT程序的命令行参数
码农飞飞
QT+QMLqtui开发语言json
在开发一些非UI程序的时候,我们习惯通过命令行参数给程序传递一些配置项和参数。这时候在程序里面解析这些配置项和参数就成了一个让人头疼的问题。其实针对QT命令行参数的解析,QT提供了现成的工具类QCommandLineParser,通过使用工具类可以极大的简化我们解析命令行参数的工作量。这里介绍一下命令行参数解析类的使用方法。获取程序的版本信息对于一些通用产品,比如git或者electron等等我们
- Unexpected token ‘o‘, “[object Obj“... is not valid JSON 报错原因解释
dongIsRunning
json前端javascript
在开发时使用到JSON.parse报错,不过第一次不会报错,解释一下原因:JSON.parse()用于从一个字符串中解析出json对象,举个例子:varstr='{"name":"Bom","age":"15"}'JSON.parse(str)//结果是一个Object//age:"15";//name:"Bom";报错的原因:因为你转换的数据本来就是object,JSON.parse()这个方法
- tiptap parseHTML renderHTML 使用
曹天骄
前端数据库
要在Tiptap中使用parseHTML和renderHTML,可以通过创建自定义扩展来解析和渲染自定义的HTML元素。这两个方法允许你定义如何将HTML解析为ProseMirror文档节点以及如何将ProseMirror的文档节点渲染为HTML。1.parseHTMLparseHTML用于将HTML元素解析为ProseMirror节点。在自定义扩展中,你可以定义如何将特定的HTML元素解析为Ti
- sql存储过程中处理json数据
taozi_5188
sql常用功能和代码json存储jsonsql函数
注意:此方法经过验证后,在数据量大于5条以后会很慢,不建议使用。建议使用这种方法:https://blog.csdn.net/taozi_5188/article/details/105744265用到的函数:CREATEFUNCTION[huo].[parseJSON](@JSONNVARCHAR(MAX))RETURNS@hierarchyTABLE(element_idINTIDENTITY
- 使用C++编写接口调用PyTorch模型,并生成DLL供.NET使用
编程日记✧
pytorch人工智能python.netc#c++
一、将PyTorch模型保存为TorchScript格式1)构造一个pytorch2TorchScript.py,示例代码如下:importtorchimporttorch.nnasnnimportargparsefromnetworks.seg_modelingimportmodelasViT_segfromnetworks.seg_modelingimportCONFIGSasCONFIGS_
- Python全栈 part02 - 006 Ajax
drfung
JSON定义:JSON(Javascriptobjectnotation,JS对象标记)是一种轻量级的数据交换格式;是基于ECMASCript(w3cjs规范)的一个子集.JS-JSON-Python.pngJSON对象定义需要注意的点属性名必须用"(双引号)不能使用十六进制值不能使用undefined不能使用函数名和日期函数stringify与parse方法JSON.parse()将一个JSON
- js获取地址栏中的指定参数
puxiaotaoc
varparseQueryString=function(url,key){varnum=url.indexOf('?');//获取?的下标if(num>0){url=url.slice(num+1);//截取url?后面的所有参数vararr=url.split('&');//将各个参数放到数组里console.log(arr);varresult={};//存放结果for(vari=0;i0)
- Css-loader安装失败,webpack打包css文件时,确认css-loader和style-loader安装正确,import路径都正确,打包反复报错...
Malong Wu
Css-loader安装失败
webpack打包css文件时,确认css-loader和style-loader都安装正确,且import路径都正确,打包反复报错:ERRORin./src/assets/styles/test.css1:0Moduleparsefailed:Unexpectedtoken(1:0)Youmayneedanappropriateloadertohandlethisfiletype,current
- JS手写实现深拷贝
Mzp风可名喜欢
javascript前端
手写深拷贝一、通过JSON.stringify二、函数库lodash三、递归实现深拷贝基础递归升级版递归---解决环引用爆栈问题最终版递归---解决其余类型拷贝结果一、通过JSON.stringifyJSON.parse(JSON.stringify(obj))是比较常用的深拷贝方法之一原理:利用JSON.stringify将JavaScript对象序列化成为JSON字符串,并将对象里面的内容转换
- java parser乱码_HtmlParser 2.0 中文乱码问题
福建低调
javaparser乱码
对于HTMLParser2.0工具包我们需要修改其中的Page.java文件使其适用中文的html文件分析。主要是把protectedstaticfinalStringDEFAULT_CHARSET="ISO-8859-1";修改成protectedstaticfinalStringDEFAULT_CHARSET="gb2312";主要是兼容charset='GBK'声明的页面。--因为采用默认的
- OmniParse:解锁生成式AI潜能的全能数据解析框架
花生糖@
AIGC学习资源人工智能AI代码AI实战
在当今信息爆炸的时代,非结构化数据如潮水般涌来,而如何有效驾驭这些数据,使之成为驱动智能应用的燃料,成为了业界亟待解决的挑战。在此背景下,OmniParse应运而生,作为一个开源框架,它致力于将复杂的非结构化数据转化为生成式AI应用所需的清晰、可操作的结构化数据。本文将深入剖析OmniParse的核心优势与特性,探讨其如何赋能AI+PDF工具、知识库产品的开发,以及其在各行业的潜在应用价值。一、核
- Biopython从pdb文件中提取蛋白质链的信息
qq_27390023
开发语言python
使用Biopython的PDB模块可以方便地解析PDB文件并提取你需要的信息。下面是一个示例代码,用于提取PDB文件中的链名称、序列和长度:示例代码fromBioimportPDB#读取PDB文件pdb_file="/Users/zhengxueming/Downloads/1a0h.pdb"parser=PDB.PDBParser(QUIET=True)structure=parser.get_
- 微信小程序 js 计算时间间隔
XUE_雪
微信小程序javascript
/**判断距离当前时间间隔多少分钟*/judgeTimeDiffer:function(startTime){varstartTimes=newDate(startTime.replace(/-/g,'/'));returnparseInt((startTimes.getTime()-newDate().getTime())/1000/60);},切记:要将时间格式通过replace(/-/g,'
- JSON parse error: Illegal character ((CTRL-CHAR, code 31)): only regular white space (\r, \n, \t)
Chen__Wu
javajavajson
JSONparseerror:Illegalcharacter((CTRL-CHAR,code31)):onlyregularwhitespace(\r,\n,\t)isallowedbetweentokens;nestedexceptioniscom.fasterxml.jackson.core.JsonParseException:Illegalcharacter((CTRL-CHAR,cod
- Webpack4-配置
16325
module.rule.parser解析选项对象。所有应用的解析选项都将合并。解析器(parser)可以查阅这些选项,并相应地禁用或重新配置。大多数默认插件,会如下解释值:将选项设置为false,将禁用解析器。将选项设置为true,或不修改将其保留为undefined,可以启用解析器。然而,一些解析器(parser)插件可能不光只接收一个布尔值。例如,内部的NodeStuffPlugin差距,可以
- HTML到React解析器 - 使用指南及教程
罗昭贝Lovely
HTML到React解析器-使用指南及教程html-react-parser:memo:HTMLtoReactparser.项目地址:https://gitcode.com/gh_mirrors/ht/html-react-parser一、项目介绍HTML到React解析器(html-react-parser)是由remarkablemark开发的一款开源工具库,专为将普通的HTML字符串转换成R
- Autoencoder
chuange6363
人工智能python
自编码器Autoencoder稀疏自编码器SparseAutoencoder降噪自编码器DenoisingAutoencoder堆叠自编码器StackedAutoencoder本博客是从梁斌博士的博客上面复制过来的,本人利用Tensorflow重新实现了博客中的代码深度学习有一个重要的概念叫autoencoder,这是个什么东西呢,本文通过一个例子来普及这个术语。简单来说autoencoder是一
- 多线程编程之join()方法
周凡杨
javaJOIN多线程编程线程
现实生活中,有些工作是需要团队中成员依次完成的,这就涉及到了一个顺序问题。现在有T1、T2、T3三个工人,如何保证T2在T1执行完后执行,T3在T2执行完后执行?问题分析:首先问题中有三个实体,T1、T2、T3, 因为是多线程编程,所以都要设计成线程类。关键是怎么保证线程能依次执行完呢?
Java实现过程如下:
public class T1 implements Runnabl
- java中switch的使用
bingyingao
javaenumbreakcontinue
java中的switch仅支持case条件仅支持int、enum两种类型。
用enum的时候,不能直接写下列形式。
switch (timeType) {
case ProdtransTimeTypeEnum.DAILY:
break;
default:
br
- hive having count 不能去重
daizj
hive去重having count计数
hive在使用having count()是,不支持去重计数
hive (default)> select imei from t_test_phonenum where ds=20150701 group by imei having count(distinct phone_num)>1 limit 10;
FAILED: SemanticExcep
- WebSphere对JSP的缓存
周凡杨
WAS JSP 缓存
对于线网上的工程,更新JSP到WebSphere后,有时会出现修改的jsp没有起作用,特别是改变了某jsp的样式后,在页面中没看到效果,这主要就是由于websphere中缓存的缘故,这就要清除WebSphere中jsp缓存。要清除WebSphere中JSP的缓存,就要找到WAS安装后的根目录。
现服务
- 设计模式总结
朱辉辉33
java设计模式
1.工厂模式
1.1 工厂方法模式 (由一个工厂类管理构造方法)
1.1.1普通工厂模式(一个工厂类中只有一个方法)
1.1.2多工厂模式(一个工厂类中有多个方法)
1.1.3静态工厂模式(将工厂类中的方法变成静态方法)
&n
- 实例:供应商管理报表需求调研报告
老A不折腾
finereport报表系统报表软件信息化选型
引言
随着企业集团的生产规模扩张,为支撑全球供应链管理,对于供应商的管理和采购过程的监控已经不局限于简单的交付以及价格的管理,目前采购及供应商管理各个环节的操作分别在不同的系统下进行,而各个数据源都独立存在,无法提供统一的数据支持;因此,为了实现对于数据分析以提供采购决策,建立报表体系成为必须。 业务目标
1、通过报表为采购决策提供数据分析与支撑
2、对供应商进行综合评估以及管理,合理管理和
- mysql
林鹤霄
转载源:http://blog.sina.com.cn/s/blog_4f925fc30100rx5l.html
mysql -uroot -p
ERROR 1045 (28000): Access denied for user 'root'@'localhost' (using password: YES)
[root@centos var]# service mysql
- Linux下多线程堆栈查看工具(pstree、ps、pstack)
aigo
linux
原文:http://blog.csdn.net/yfkiss/article/details/6729364
1. pstree
pstree以树结构显示进程$ pstree -p work | grep adsshd(22669)---bash(22670)---ad_preprocess(4551)-+-{ad_preprocess}(4552) &n
- html input与textarea 值改变事件
alxw4616
JavaScript
// 文本输入框(input) 文本域(textarea)值改变事件
// onpropertychange(IE) oninput(w3c)
$('input,textarea').on('propertychange input', function(event) {
console.log($(this).val())
});
- String类的基本用法
百合不是茶
String
字符串的用法;
// 根据字节数组创建字符串
byte[] by = { 'a', 'b', 'c', 'd' };
String newByteString = new String(by);
1,length() 获取字符串的长度
&nbs
- JDK1.5 Semaphore实例
bijian1013
javathreadjava多线程Semaphore
Semaphore类
一个计数信号量。从概念上讲,信号量维护了一个许可集合。如有必要,在许可可用前会阻塞每一个 acquire(),然后再获取该许可。每个 release() 添加一个许可,从而可能释放一个正在阻塞的获取者。但是,不使用实际的许可对象,Semaphore 只对可用许可的号码进行计数,并采取相应的行动。
S
- 使用GZip来压缩传输量
bijian1013
javaGZip
启动GZip压缩要用到一个开源的Filter:PJL Compressing Filter。这个Filter自1.5.0开始该工程开始构建于JDK5.0,因此在JDK1.4环境下只能使用1.4.6。
PJL Compressi
- 【Java范型三】Java范型详解之范型类型通配符
bit1129
java
定义如下一个简单的范型类,
package com.tom.lang.generics;
public class Generics<T> {
private T value;
public Generics(T value) {
this.value = value;
}
}
- 【Hadoop十二】HDFS常用命令
bit1129
hadoop
1. 修改日志文件查看器
hdfs oev -i edits_0000000000000000081-0000000000000000089 -o edits.xml
cat edits.xml
修改日志文件转储为xml格式的edits.xml文件,其中每条RECORD就是一个操作事务日志
2. fsimage查看HDFS中的块信息等
&nb
- 怎样区别nginx中rewrite时break和last
ronin47
在使用nginx配置rewrite中经常会遇到有的地方用last并不能工作,换成break就可以,其中的原理是对于根目录的理解有所区别,按我的测试结果大致是这样的。
location /
{
proxy_pass http://test;
- java-21.中兴面试题 输入两个整数 n 和 m ,从数列 1 , 2 , 3.......n 中随意取几个数 , 使其和等于 m
bylijinnan
java
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
public class CombinationToSum {
/*
第21 题
2010 年中兴面试题
编程求解:
输入两个整数 n 和 m ,从数列 1 , 2 , 3.......n 中随意取几个数 ,
使其和等
- eclipse svn 帐号密码修改问题
开窍的石头
eclipseSVNsvn帐号密码修改
问题描述:
Eclipse的SVN插件Subclipse做得很好,在svn操作方面提供了很强大丰富的功能。但到目前为止,该插件对svn用户的概念极为淡薄,不但不能方便地切换用户,而且一旦用户的帐号、密码保存之后,就无法再变更了。
解决思路:
删除subclipse记录的帐号、密码信息,重新输入
- [电子商务]传统商务活动与互联网的结合
comsci
电子商务
某一个传统名牌产品,过去销售的地点就在某些特定的地区和阶层,现在进入互联网之后,用户的数量群突然扩大了无数倍,但是,这种产品潜在的劣势也被放大了无数倍,这种销售利润与经营风险同步放大的效应,在最近几年将会频繁出现。。。。
如何避免销售量和利润率增加的
- java 解析 properties-使用 Properties-可以指定配置文件路径
cuityang
javaproperties
#mq
xdr.mq.url=tcp://192.168.100.15:61618;
import java.io.IOException;
import java.util.Properties;
public class Test {
String conf = "log4j.properties";
private static final
- Java核心问题集锦
darrenzhu
java基础核心难点
注意,这里的参考文章基本来自Effective Java和jdk源码
1)ConcurrentModificationException
当你用for each遍历一个list时,如果你在循环主体代码中修改list中的元素,将会得到这个Exception,解决的办法是:
1)用listIterator, 它支持在遍历的过程中修改元素,
2)不用listIterator, new一个
- 1分钟学会Markdown语法
dcj3sjt126com
markdown
markdown 简明语法 基本符号
*,-,+ 3个符号效果都一样,这3个符号被称为 Markdown符号
空白行表示另起一个段落
`是表示inline代码,tab是用来标记 代码段,分别对应html的code,pre标签
换行
单一段落( <p>) 用一个空白行
连续两个空格 会变成一个 <br>
连续3个符号,然后是空行
- Gson使用二(GsonBuilder)
eksliang
jsongsonGsonBuilder
转载请出自出处:http://eksliang.iteye.com/blog/2175473 一.概述
GsonBuilder用来定制java跟json之间的转换格式
二.基本使用
实体测试类:
温馨提示:默认情况下@Expose注解是不起作用的,除非你用GsonBuilder创建Gson的时候调用了GsonBuilder.excludeField
- 报ClassNotFoundException: Didn't find class "...Activity" on path: DexPathList
gundumw100
android
有一个工程,本来运行是正常的,我想把它移植到另一台PC上,结果报:
java.lang.RuntimeException: Unable to instantiate activity ComponentInfo{com.mobovip.bgr/com.mobovip.bgr.MainActivity}: java.lang.ClassNotFoundException: Didn't f
- JavaWeb之JSP指令
ihuning
javaweb
要点
JSP指令简介
page指令
include指令
JSP指令简介
JSP指令(directive)是为JSP引擎而设计的,它们并不直接产生任何可见输出,而只是告诉引擎如何处理JSP页面中的其余部分。
JSP指令的基本语法格式:
<%@ 指令 属性名="
- mac上编译FFmpeg跑ios
啸笑天
ffmpeg
1、下载文件:https://github.com/libav/gas-preprocessor, 复制gas-preprocessor.pl到/usr/local/bin/下, 修改文件权限:chmod 777 /usr/local/bin/gas-preprocessor.pl
2、安装yasm-1.2.0
curl http://www.tortall.net/projects/yasm
- sql mysql oracle中字符串连接
macroli
oraclesqlmysqlSQL Server
有的时候,我们有需要将由不同栏位获得的资料串连在一起。每一种资料库都有提供方法来达到这个目的:
MySQL: CONCAT()
Oracle: CONCAT(), ||
SQL Server: +
CONCAT() 的语法如下:
Mysql 中 CONCAT(字串1, 字串2, 字串3, ...): 将字串1、字串2、字串3,等字串连在一起。
请注意,Oracle的CON
- Git fatal: unab SSL certificate problem: unable to get local issuer ce rtificate
qiaolevip
学习永无止境每天进步一点点git纵观千象
// 报错如下:
$ git pull origin master
fatal: unable to access 'https://git.xxx.com/': SSL certificate problem: unable to get local issuer ce
rtificate
// 原因:
由于git最新版默认使用ssl安全验证,但是我们是使用的git未设
- windows命令行设置wifi
surfingll
windowswifi笔记本wifi
还没有讨厌无线wifi的无尽广告么,还在耐心等待它慢慢启动么
教你命令行设置 笔记本电脑wifi:
1、开启wifi命令
netsh wlan set hostednetwork mode=allow ssid=surf8 key=bb123456
netsh wlan start hostednetwork
pause
其中pause是等待输入,可以去掉
2、
- Linux(Ubuntu)下安装sysv-rc-conf
wmlJava
linuxubuntusysv-rc-conf
安装:sudo apt-get install sysv-rc-conf 使用:sudo sysv-rc-conf
操作界面十分简洁,你可以用鼠标点击,也可以用键盘方向键定位,用空格键选择,用Ctrl+N翻下一页,用Ctrl+P翻上一页,用Q退出。
背景知识
sysv-rc-conf是一个强大的服务管理程序,群众的意见是sysv-rc-conf比chkconf
- svn切换环境,重发布应用多了javaee标签前缀
zengshaotao
javaee
更换了开发环境,从杭州,改变到了上海。svn的地址肯定要切换的,切换之前需要将原svn自带的.svn文件信息删除,可手动删除,也可通过废弃原来的svn位置提示删除.svn时删除。
然后就是按照最新的svn地址和规范建立相关的目录信息,再将原来的纯代码信息上传到新的环境。然后再重新检出,这样每次修改后就可以看到哪些文件被修改过,这对于增量发布的规范特别有用。
检出
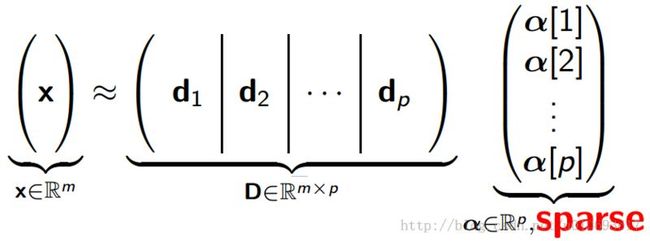
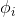 such that an input vector can be represented as a linear combination of these basis vectors:
such that an input vector can be represented as a linear combination of these basis vectors:
 are better able to capture structures and patterns inherent in the input data
are better able to capture structures and patterns inherent in the input data  .
. 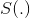 is a sparsity function which penalizes
is a sparsity function which penalizes 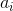 for being far from zero. We can interpret the first term of the sparse coding objective as a reconstruction term which tries to force the algorithm to provide a good representation of
for being far from zero. We can interpret the first term of the sparse coding objective as a reconstruction term which tries to force the algorithm to provide a good representation of  , and the second term as a sparsity penalty which forces our representation of
, and the second term as a sparsity penalty which forces our representation of  (i.e., the learned features) to be sparse. The constant
(i.e., the learned features) to be sparse. The constant  is a scaling constant to determine the relative importance of these two contributions.
is a scaling constant to determine the relative importance of these two contributions.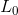 norm, it is non-differentiable and difficult to optimize in general. In practice, common choices for the sparsity cost
norm, it is non-differentiable and difficult to optimize in general. In practice, common choices for the sparsity cost 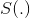 are the
are the 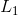 penalty and the log sparsity
penalty and the log sparsity
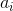 and scaling up
and scaling up 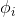 by some large constant. To prevent this from happening, we will constrain
by some large constant. To prevent this from happening, we will constrain  to be less than some constant
to be less than some constant 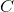 . The full sparse coding cost function hence is:
where the constant is usually set
. The full sparse coding cost function hence is:
where the constant is usually set
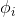 small:
small:
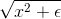 in place of
in place of 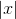 , where
, where  is a "smoothing parameter" which can also be interpreted as a sort of "sparsity parameter" (to see this, observe that when
is a "smoothing parameter" which can also be interpreted as a sort of "sparsity parameter" (to see this, observe that when  is large compared to
is large compared to  , the
, the  is dominated by
is dominated by  , and taking the square root yield approximately
, and taking the square root yield approximately  .
. 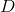 ).
). 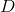 is "adapted" to
is "adapted" to  if it can represent it with a few basis vectors, that is, there exists a sparse vector
if it can represent it with a few basis vectors, that is, there exists a sparse vector  in
in 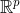 such that . We call
such that . We call  the sparse code. It is illustrated as follows:
the sparse code. It is illustrated as follows:
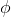 using sparse coding consists of performing two separate optimizations (i.e., alternative optimization method):
using sparse coding consists of performing two separate optimizations (i.e., alternative optimization method):
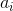 for each training example
for each training example
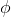 across many training examples at once.
across many training examples at once. can achieve good results, but very slow.
can achieve good results, but very slow.