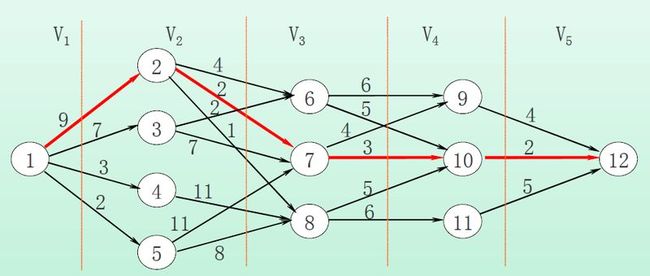
多段图算法

COST(i,j)=min{c(j,v) + COST(i+1,v)}
　　(v∈Vk+1，<j,v>∈E)

COST(3,6) = min{6+COST(4,9), 5+COST(4,10)} = 7 (已知COST(4,9)=4，COST(4,10)=2)
COST(3,7) = min{4+COST(4,9), 3+COST(4,10)}= 5
COST(3,8) = 7
COST(2,2) = min{4+COST(3,6), 2+COST(3,7), 1+COST(3,8)}= 7
COST(2,3) = 9
COST(2,4) = 18
COST(2,5) = 15
COST(1,1) = min{9+COST(2,2), 7+COST(2,3),3+COST(2,4), 2+COST(2,5)}= 16
于是，由s到t的最小成本路径的成本为16。

 

多段图的向前处理算法：
line void FGraph (edgeType E, int k, int n, int P[]) {
//输人按段顺序给结点编号的有n个结点的k段图。E是边集，
//c(i,j)是边<i,j>的成本。P(1:k)是最小成本路径。

1 float COST[n]；int D[n-1], r, j；
2 COST[n]=0；
3 for(j=n-1；j>=1；--j) { //计算COST(j)
4 设r是一个这样的结点，<i,j>∈E且使c(j,r)+COST[r]取最小值；
5 COST[j] = c[j,r] + COST[r]；
6 D[j]=r；
7 }；//找一条最小成本路径
8 P[1]=1；p[k]=n；
9 for(j=2；j<=k-1；++j){ //找路径上的第j个结点
10 P[j] = D[P[j-l]]；
11 }；//for
12 }//FGraph

　　如果G用邻接表表示，那么第4行的r可以在与结点j的度成正比的时间内算出。因此，如果G有e条边，则第3～7行的for循环的时间是Θ(n+e)，第9～11行的for循环时间是Θ(k)。总的计算时间在Θ(n+e)以内。除了输人所需要的空间外，还需要给COST，D和P分配空间。

 

BCOST(i,j)=min｛BCOST(i-1,v)+c(v,j)｝

　　(v∈Vi-1，<v , j>∈E)

BCOST(3,6) = min{BCOST(2,2)+4,BCOST(2,3)+2}= 9
BCOST(3,7) = 11
BCOST(3,8) = 10
BCOST(4,9) = min{BCOST(3,6)+6,BCOST(3,7)+4}= 15
BCOST(4,10) = min{COST(3,6)+5,BCOST(3,7)+3,BCOST(3,8)+5}=14
BCOST(4,11) = 16
BCOST(5,12) = min{BCOST(4,9)+4,BCOST(4,10)+2,BCOST(4,11)+5}=16

　获取s到t的一条最小成本路径的向后处理算法是函数BGraph。它与FGraph一样，略去了BCOST，P和D的第一个下标。只要G用它的逆邻接表表示，即对于每一个结点v，有一个使得<w,v>∈E的结点w的链接表。

　

多段图的向后处理算法：

Line void BGRAPH(edgeType E, int k, int n, int BP[]) {
//和FGraph功能相同
float BCOST[n]；int D[n-1]，r，j；

1 BCOST[1] = 0；
2 For(j=2；j<=n；++j) { 计算BCOST(j)
3 设r是一个这样的结点，<i,j>∈E且使BCOST[r]+c[r,j]取最小值；
4 BCOST[j] = BCOST[r] + c[r,j]；
5 D[j] = r；
6 };//for
//找一条最小成本路径
7 BP[1] = 1；BP[k] = n；
8 for(j=k-1；j>=2；--j) {//找路径上的第j个结点
9 BP[j]=D[BP[j+1]]
10 }；//for
11 }//BGraph

不难看出，即使对多段图的更一般形式，即图中允许有这样的边<u,v>，其中u∈Vi，v∈Vj且i<j，FGraph和BGraph都能正确地运行。