POJ1408-Fishnet

转载请注明出处：優YoU http://user.qzone.qq.com/289065406/blog/1302523813 

大致题意：

一个1X1的正方形，每条边上有n个不同的点（不包括顶点），并给出它们的坐标。现在把对边相对应的点相连，将正方形分割成(n+1)*(n+1)个小四边形。问最大的四边形的面积是多少。

 

解题思路：

计算几何求面积的题，算半条水题吧。。

基本思路：

构造所有的线段，然后枚举每对水平－竖直线段，求交点，然后计算四边形面积，求最大值。

 

应用知识：

叉积（规范相交）

多边形分解

三角形基于计算几何的面积公式（注意正负）

 

我先建立一个数学模型说明问题：

以n=3为例画图 （当然实际上内部的线不一定是正交的，这里只是为了简单说明）

 

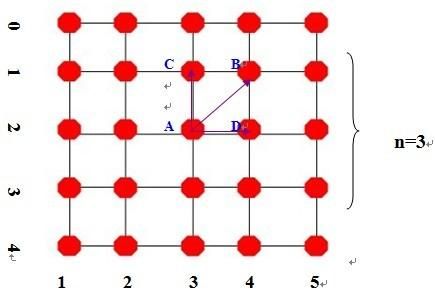
第一步建立一个大小为 (n+2)*(n+2) 的二维交点矩阵node，每个元素存储一个交点坐标(x,y)

由于四角交点为定点，每条边上的交点又是输入值，那么外围一圈的交点都是已知了

由于对边的点是对应相连的，因此要求的就是内部n*n个交点

显然地，所求的所有交点都是某两条直线规范相交所得，因此就可以直接使用求规范相交的交点的公式，而不需要套用模板了

交点公式 (及推导过程) 请参看  刘汝佳《算法艺术与信息学竞赛》P357 这里不再说明

 

通过两两枚举所有内部直线，就能得到 交点矩阵node[][]

 

那么剩下的问题就是求出所有 简单四边形（不包含其他四边形） 的面积，输出最大的一个。那么问题就是：已知一个不规则四边形四个角的坐标，求它的面积

 

由于四边形是不规则的，直接求解其面积是非常困难的，唯有将其划分为两个三角形，分别求出两个三角形的面积，再相加

 

如图，我求解所有四边形时都是采用如图的划分方法

那么问题进一步转化为“已知不规则三角形三个角的坐标，如何求其面积”

不用比较都看得出，计算几何的方法远远优于解析几何，不但省去计算一堆长度的麻烦（避免了精度误差），而且还能利用计算交点时 计算叉积的功能函数cross（）

使用计算几何，不但运算量大大减少了，代码也写少了，结果还更精确

 

不过有一点要注意的是，计算几何计算的面积是有方向的，即面积可能为负，所以绝对值必不可少，这点千万注意

  1 //Memory Time 
  2 //544K   16MS 
  3 
  4 #include<iostream>
  5 #include<cmath>
  6 #include<iomanip>
  7 using namespace std;
  8 
  9 typedef class Node
 10 {
 11     public:
 12         double x,y;
 13 }location;
 14 
 15 double det(double x1,double y1,double x2,double y2)
 16 {
 17     return x1*y2-x2*y1;
 18 }
 19 
 20 double cross(location A,location B,location C,location D)       //计算 AB x CD
 21 {
 22     return det(B.x-A.x , B.y-A.y , D.x-C.x , D.y-C.y);
 23 }
 24 
 25 /*Compute Intersection*/
 26 
 27 double xx,yy;  //坐标返回值
 28 void intersection(location A,location B,location C,location D)
 29 {
 30     double area1=cross(A,B,A,C);
 31     double area2=cross(A,B,A,D);
 32 
 33     xx=(area2*C.x - area1*D.x)/(area2-area1);    //本题所求的交点一定是规范相交所得，因此无需判断是否规范相交
 34     yy=(area2*C.y - area1*D.y)/(area2-area1); 
 35     return;
 36 }
 37 
 38 /*Compute Area*/
 39 
 40 double area(location A,location B,location C,location D)
 41 {
 42     double triangle1=fabs(0.5*cross(A,B,A,C));    //用计算几何的方法计算的面积是有向面积
 43     double triangle2=fabs(0.5*cross(A,B,A,D));    //即算出来的面积可能为负数，因此必须用绝对值
 44                                                   // fabs() 为取double的绝对值函数
 45     return triangle1+triangle2;
 46 }
 47 
 48 int main(int i,int j,int k)
 49 {
 50     int n;
 51     while(cin>>n)
 52     {
 53         if(!n)
 54             break;
 55 
 56         /*Initial*/
 57 
 58         location** node=new location*[n+2];
 59         node[0]=new location[n+2];   //下边
 60         node[n+1]=new location[n+2]; //上边
 61 
 62         /*Input Down-edge*/
 63 
 64         node[0][0].x = node[0][0].y =0.0;
 65         for(i=1;i<=n;i++)
 66         {
 67             cin>>node[0][i].x;
 68             node[0][i].y=0.0;
 69         }
 70         node[0][n+1].x=1.0;
 71         node[0][n+1].y=0.0;
 72 
 73         /*Input Up-edge*/
 74 
 75         node[n+1][0].x=0.0;
 76         node[n+1][0].y=1.0;
 77         for(i=1;i<=n;i++)
 78         {
 79             cin>>node[n+1][i].x;
 80             node[n+1][i].y=1.0;
 81         }
 82         node[n+1][n+1].x=1.0;
 83         node[n+1][n+1].y=1.0;
 84 
 85         /*Input Left-edge*/
 86 
 87         for(i=1;i<=n;i++)
 88         {
 89             node[i]=new location[n+2];
 90             cin>>node[i][0].y;
 91             node[i][0].x=0.0;
 92         }
 93 
 94         /*Input right-edge*/
 95 
 96         for(i=1;i<=n;i++)
 97         {
 98             cin>>node[i][n+1].y;
 99             node[i][n+1].x=1.0;
100         }
101 
102         /*Compute Intersection*/
103 
104         for(j=1;j<=n;j++)
105             for(i=1;i<=n;i++)
106             {
107                 intersection(node[0][j],node[n+1][j],node[i][0],node[i][n+1]);
108                 node[i][j].x=xx;
109                 node[i][j].y=yy;
110             }
111 
112         /*Compute Area*/
113 
114         double max_area=0.0;
115 
116         for(i=1;i<=n+1;i++)
117             for(j=1;j<=n+1;j++)
118             {
119                 double temp=area(node[i-1][j-1],node[i][j],node[i][j-1],node[i-1][j]);
120                 if(max_area < temp)
121                     max_area = temp;
122             }
123 
124 
125         /*Output*/
126 
127         cout<<fixed<<setprecision(6)<<max_area<<endl;
128 
129         /*Realx Room*/
130 
131         delete[] node;
132     }
133     return 0;
134 }