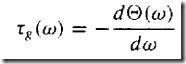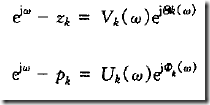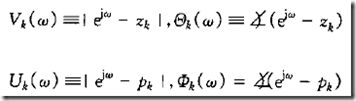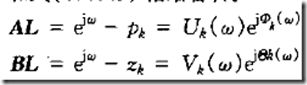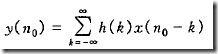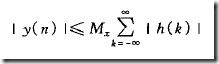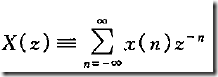频率选择滤波器 线性时不变系统
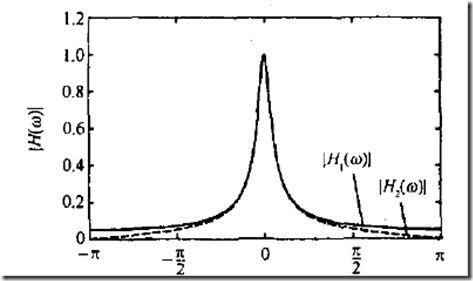
通常线性是不变系统根据频率响应H(w)来改变输入信号频谱X(w)，产生的频谱为：Y(w) = H(w)X(w)的输出信号
首先看下理想滤波器
给图给真相：
理想滤波器特性：
1、具有常数增益的带通特性，带阻部分增益为0；
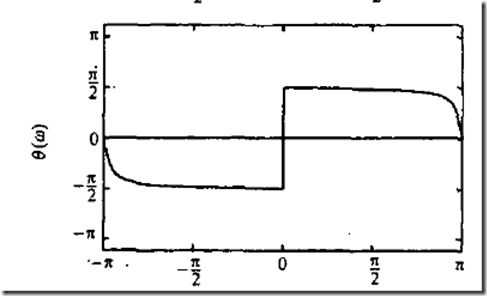
2、线性相位响应。
来看下线性相位响应产生的原因：
例子：
理想滤波器频率响应：
（常数增益的带通特性，带阻部分增益为0）
输出信号：
傅里叶变换的缩放与时移性
可见滤波器输出只是幅度缩放与延时 不认为是信号失真
这里提到的时移性这儿来回顾下：
时间域向右平移相当于相位减小即矢量顺时针旋转
这儿有个’单位延时‘概念 即相位对频率的倒数
（相频特性： 
）
求到后为常数n 可见所有输出的频率分量的延迟都一样
总结：理想滤波器有线性相频特性，有常数幅频特性
理想滤波器的冲击响应：
1.可见此滤波器非因果也不绝对可和 故是不稳定的，不可物理实现。（附录A B）
在Z平面放置 零点 极点 改变 频率响应 从而实现 简单滤波器设计
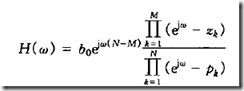
首先看下频率响应函数的计算(零极点方式)
两边同乘e
用复数形式表示 可分解出相位与幅值
幅值：
各项幅值相乘
相位：
相角为相加 都是乘 
矢量正方向旋转
除号为
的-1次幂 矢量反方向旋转 相角相减
Z:零点
P:极点
可见知道零极点就可以计算出频率响应
几何解释：（力推）
A:极点
B：零点
L:由w确定的e
这个式子的向量表示
得：
相角相减
幅值相除
总结：L随着频率在变
可见当频率靠近零点时 响应的幅值变小（做分母的缘故）
当频率靠近极点时 响应的幅值变大（做分子）
在极点附近放零点可以抵消极点影响 ，反之依然
啦啦啦 数字滤波器 出现啦！！！！
了解啦零极点对频率响应的影响 来看下则么运用这些性质设计我么想要的滤波器。
重中之重：
放置零极点的基本原则：
在单位圆上 对需要 加强的频率点附近加上极点 对需要减弱的频率点附近加上零点。为啦系统可实现性 还有两条约束
1.为了使系统稳定 所有极点必须放置在单位圆内，而零点没要求 WHY?（附录C）
2.是滤波器系数是实数 所有复数的零点与极点必须以共轭复数形式出现。（相乘为实数嘛）
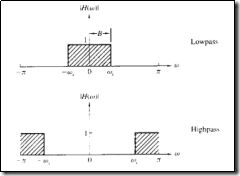
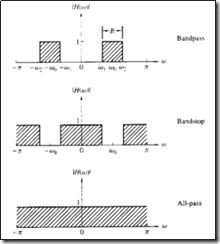
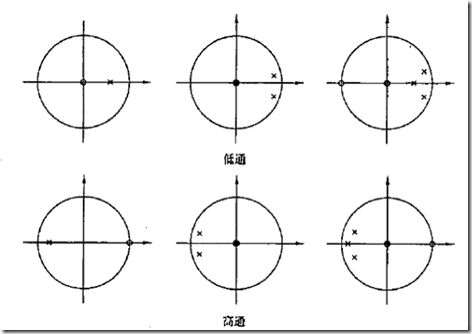
低通 高通 滤波器
幅频 相频关系：
低通：
在-1处加零点可使 角频率为
的幅值降为零
高通：低通零极点对折 (虚轴)
至于因果性如何 推出 前两结论 （待学习）
实际滤波器特性：
设计要求：
最大允许带通纹波
最大允许带阻纹波
带通截止频率
带阻截止频率
相关概念回顾
附录A
因果系统定义：
它在n时刻的输出只依赖当前与故去的输入而不依赖将来的输入
如何验证因果性：
在线性时不变系统中 因果性可以看做是冲击响应的范围的条件
来看下n=n0的输入输出关系：同样用到卷积公式：
根据因果的定义展开：
根具定义大于N0的输出部分应该为0；因此冲击响应h小于0部分应为0.
总结：一个LTI系统是因果的，当且仅当它的冲击响应在N为负时为0；
因果性的必须性: 在实时信号处理中 我们无法获得输入信号的将来值
在计算当前的输出时我们只有当前与过去的输入值可用。
附录B
稳定性：
BIBO稳定：当且仅当任何有界输入X 他的输出序列Y都是有界的。
如何来验证BIBO：
X有界：
通过卷积公式联系X,Y
绝对值不等式转换;
带入X的边界值
我们要保证的是Y 有边界值
则：
冲击响应要 绝对可和
附录C
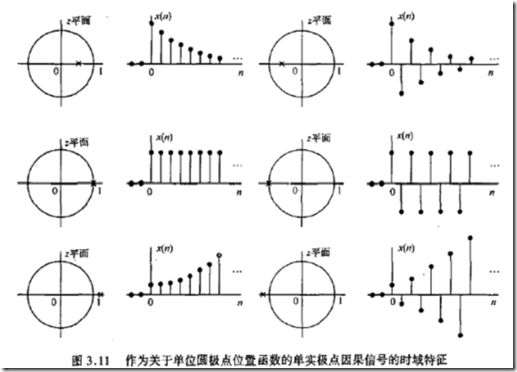
因果信号的时域行为与极点位置
因果信号的内容可用于因果LTI系统 因为 此系统的脉冲响应是因果信号
观点：因果信号的行为特性取决于他的极点的位置
极点：是指一个z值使使的X(z)为无穷
我们关注无穷而没关注0是应为 稳定性的定义（BIBO） 要有限要收敛 不可无穷。
无穷与有限只是一步之隔，来看下
Z变化的定义;
当极点>1时这不符合BIBO，不是我们想要的 无界导致数字系统的丄溢。
极点离原点越近 衰减越快
这里给出两个例子：
