【vijos】1781 同余方程（拓展欧几里得）

https://vijos.org/p/1781

学习了下拓欧。。

求exgcd时，因为

a*x1+b*y1=a*x2+b*y2=b*x2+(a-b*[a/b])*y2

然后移项得

a*x1+b*y1=b*x2+a*y2-(b*[a/b])*y2

a*(x1-y2)+b*y1-b*x2+(b*[a/b]*y2)=0

a*(x1-y2)+b*(y1-x2+[a/b]*y2)=0

所以

x1=y2, y1=x2-[a/b]*y2（sigh。。我也不知道为什么诶。难道(x1-y2)等于b且(y1-x2+[a/b]*y2)等于-a的情况不行么）

然后求出一组解x0和y0后因为ax0+by0=ax1+by1移项得a(x0-x1)=b(y1-y0)除以d=gcd(a,b)后，设a0=a/d, b0=b/d，可知a0和b0互质，原式变为

a0(x0-x1)=b0(y1-y0)

因为a0和b0互质，要想等式成立，有x0-x1=b0, y1-y0=a0所以x1=x0-b0=x0-b/d；y1=y0+a0=y0+a/d然后就可以得出所有解啦。。。

回到本题，这题可以转换为ax-by=1等式这可以等同于ax+by=1（只是y的符号变了而已）所以我们用拓欧求出来就行了

而非负整数解x可以由x=(x0+b/gcd(a, b))%(b/gcd(a, b)得到

对于方程ax+by=c我们求出来ax+by=(a,b)后求出原方程的解可以这样做

（从而接触到了“不定方程”这东西，，，这是啥，，，以后有时间看看（《初等数论》上有详细介绍）， http://baike.baidu.com/view/375208.htm?fr=aladdin

 

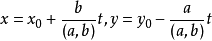
#include <cstdio>

#include <cstring>

#include <cmath>

#include <string>

#include <iostream>

#include <algorithm>

#include <queue>

using namespace std;

#define rep(i, n) for(int i=0; i<(n); ++i)

#define for1(i,a,n) for(int i=(a);i<=(n);++i)

#define for2(i,a,n) for(int i=(a);i<(n);++i)

#define for3(i,a,n) for(int i=(a);i>=(n);--i)

#define for4(i,a,n) for(int i=(a);i>(n);--i)

#define CC(i,a) memset(i,a,sizeof(i))

#define read(a) a=getint()

#define print(a) printf("%d", a)

#define dbg(x) cout << (#x) << " = " << (x) << endl

#define printarr2(a, b, c) for1(_, 1, b) { for1(__, 1, c) cout << a[_][__]; cout << endl; }

#define printarr1(a, b) for1(_, 1, b) cout << a[_] << '\t'; cout << endl

inline const int getint() { int r=0, k=1; char c=getchar(); for(; c<'0'||c>'9'; c=getchar()) if(c=='-') k=-1; for(; c>='0'&&c<='9'; c=getchar()) r=r*10+c-'0'; return k*r; }

inline const int max(const int &a, const int &b) { return a>b?a:b; }

inline const int min(const int &a, const int &b) { return a<b?a:b; }



void gcd(int a, int b, int &d, int &x, int &y) {

	if(!b) { d=a; x=1; y=0; return; }

	gcd(b, a%b, d, y, x); y-=a/b*x;

}



int main() {

	int a=getint(), b=getint();

	int x, y, d;

	gcd(a, b, d, x, y);

	print((x+b)%b);

	return 0;

}

 

 

 

---

 

 

描述

求关于x的同余方程ax ≡ 1 (mod b)的最小正整数解。

格式

输入格式

输入只有一行，包含两个正整数a, b，用一个空格隔开。

输出格式

输出只有一行，包含一个正整数x0，即最小正整数解。输入数据保证一定有解。

样例1

样例输入1[复制]

3 10

样例输出1[复制]

7

限制

每个测试点1s

提示

对于40%的数据，2 ≤b≤ 1,000；
对于60%的数据，2 ≤b≤ 50,000,000；
对于100%的数据，2 ≤a, b≤ 2,000,000,000。

来源

Noip2012提高组复赛Day2T1