POJ 3368 Frequent values 线段树与RMQ解法

题意：给出n个数的非递减序列，进行q次查询。每次查询给出两个数a，b，求出第a个数到第b个数之间数字的最大频数。

如序列：-1 -1 1 1 1 1 2 2 3

第2个数到第5个数之间出现次数最多的是数字1，它的频数3。

思路：假设查询时的参数为a, b。这道题查询时有以下两种情况：

1、 num[a] = num[b]. 即区间内的数字全相同，此时答案为b - a + 1。

2、 如果不相同，则以一般情况来讨论。见下图。

 

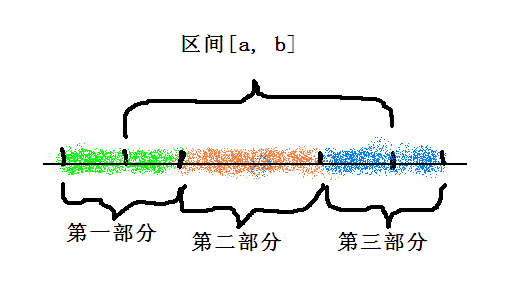
因为序列为非递减序列，因此值相同的数字必然连续出现。将区间分为3部分。num[a]以及与它值相同的区域构成第一部分，num[b]以及与它值相同的区域构成第三部分。区间[a, b]中剩下的构成第二部分。

定义left[i]表示与num[i]值相等的数字从左起开始的下标，right[i]表示与num[i]值相等的数字从右起开始的下标。

由图易知，第二部分里的数字，left与right值均在区间[a，b]内。

当给出区间范围a，b后，第一部分在区间内出现的次数为right[a] - a + 1。第三部分在区间内出现的次数为b - left[b] + 1。

如果right[a] + 1 > left[b] - 1，说明区间没有第二部分，直接输出上面两个值中的较大者。

如果存在第二部分，需要求出第二部分里的最大频数。不过这次就非常好求了，因为所有的数开始和结束都是在第二部分中，不存在部分出现的情况。定义tmax[i] = right[i] - left[i] + 1。则第二部分里数字的最大出现次数，即为该区间内tmax的最大值。将该值求出后与前面一三部分求出的较大者比较，最大的值即为最终答案。

因为查询量巨大，当第二部分需要计算时，可以采用线段树或者rmq。

现将两种方法的代码都给出。根据提交的结果来看，线段树所需空间远小于rmq，且速度稍快一点（不排除服务器的偶然性以及我rmq代码的效率比较低等原因）。

线段树求解代码

 1 #include<stdio.h>

 2 #include<algorithm>

 3 #define lson l, m, rt << 1

 4 #define rson m + 1, r, rt << 1 | 1

 5 #define maxn 100020

 6 #define inf 0x3f3f3f3f

 7 using namespace std;

 8 

 9 int num[maxn], left[maxn], right[maxn], tmax[maxn<<2];

10 void PushUp(int rt)

11 {

12     tmax[rt] = max(tmax[rt<<1], tmax[rt<<1|1]);

13 }

14 void build(int l,int r,int rt)

15 {

16     if (l == r)

17     {

18         tmax[rt] = right[l] - left[l] + 1;

19         return;

20     }

21     int m = (l + r) >> 1;

22     build(lson);

23     build(rson);

24     PushUp(rt);

25 }

26 int query(int L,int R,int l,int r,int rt)

27 {

28     if (L <= l && r <= R) return tmax[rt];

29     int m = (l + r) >> 1;

30     int ret = -inf;

31     if (L <= m) ret = max(ret, query(L, R, lson));

32     if (m < R) ret = max(ret, query(L, R, rson));

33     return ret;

34 }

35 int main()

36 {

37     int n, q;

38     //freopen("data.in", "r", stdin);

39     while (~scanf("%d",&n) && n)

40     {

41         scanf("%d",&q);

42         for (int i = 0; i < n; i++)

43         {

44             scanf("%d",&num[i]);

45             if (!i || num[i] != num[i-1]) left[i] = i;

46             else left[i] = left[i-1];

47         }

48         for (int i = n - 1; i > -1; i--)

49         {

50             if (i == (n - 1) ||num[i] != num[i+1])

51                 right[i] = i;

52             else right[i] = right[i+1];

53         }

54         build(0, n - 1, 1);

55         while (q--)

56         {

57             int a, b;

58             scanf("%d%d",&a,&b);

59             a--; b--;

60             if (num[b] == num[a]) printf("%d\n", b - a + 1);

61             else

62             {

63                 int tem = max(right[a] - a + 1, b - left[b] + 1);

64                 if (right[a] + 1 > left[b] - 1) printf("%d\n",tem);

65                 else printf("%d\n", max(tem, query(right[a] + 1, left[b] - 1, 0, n - 1, 1)));

66             }

67         }

68     }

69     return 0;

70 }

View Code

================================

rmq st算法求解代码

 1 #include<stdio.h>

 2 #include<math.h>

 3 #include<algorithm>

 4 #define maxn 100020

 5 using namespace std;

 6 

 7 int num[maxn], left[maxn], right[maxn], tmax[maxn][33];

 8 void st(int n)

 9 {

10     int k = (int)(log((double)n) / log(2.0));

11     for (int i = 0; i < n; i++)

12         tmax[i][0] = right[i] - left[i] + 1;//递推的初值

13     for (int j = 1; j <= k; j++)

14         for (int i = 0; i + (1 << j) - 1 < n; i++)

15         {

16             int m = i + (1 << (j - 1));//求出中间值

17             tmax[i][j] = max(tmax[i][j-1], tmax[m][j-1]);

18         }

19 }

20 //查询i和j之间的最值，注意i是从0开始的

21 int rmq(int i, int j)

22 {

23     int k = (int)(log(double(j - i + 1)) / log(2.0));

24     int t1 = max(tmax[i][k], tmax[j-(1<<k)+1][k]);

25     return t1;

26 }

27 int main()

28 {

29     int n, q;

30     //freopen("data.in", "r", stdin);

31     while (~scanf("%d",&n) && n)

32     {

33         scanf("%d",&q);

34         for (int i = 0; i < n; i++)

35         {

36             scanf("%d",&num[i]);

37             if (!i || num[i] != num[i-1]) left[i] = i;

38             else left[i] = left[i-1];

39         }

40         for (int i = n - 1; i > -1; i--)

41         {

42             if (i == (n - 1) ||num[i] != num[i+1])

43                 right[i] = i;

44             else right[i] = right[i+1];

45         }

46         st(n);

47         while (q--)

48         {

49             int a, b;

50             scanf("%d%d",&a,&b);

51             a--; b--;

52             if (num[b] == num[a]) printf("%d\n", b - a + 1);

53             else

54             {

55                 int tem = max(right[a] - a + 1, b - left[b] + 1);

56                 if (right[a] + 1 > left[b] - 1) printf("%d\n",tem);

57                 else printf("%d\n", max(tem, rmq(right[a] + 1, left[b] - 1)));

58             }

59         }

60     }

61     return 0;

62 }

View Code