混沌现象简介
来源: http://blog.csdn.net/kongdong/
作者:fasiondog
参考:王东生、曹磊编著,《混沌、分形及其应用》,中国科学技术大学出版社,1995年
混沌(chaos)是现代科学的重要概念,是非线性科学的一个非常重要的内容。十九世纪末和二十世纪初,庞加莱和李雅谱诺夫等人的研究,奠定了混沌学的科学基础,并激发了人们进一步探索有关的问题。混沌作为一门新兴的科学,是人类在认识大自然中的不规则性方面的一个举足重轻的突破。它已渗透到全部科学之中,其对全部科学的影响(包括自然科学及社会科学乃至哲学)所起的作用相当于微积分在十九世纪对数理工程科学的影响。人们认为,“二十世纪科学将永远铭记的只有三件事,那就是相对论、量子力学和混沌”。相对论消除了关于绝对空间与时间的幻象;量子力学消除了关于可控测量过程的牛顿式的梦;而混沌则消除了拉普拉斯关于决定论式的可预测性的幻想。
混沌现象简介
“混沌”是近代非常引人注目的热点研究,它掀起了继相对论和量子力学以来基础科学的第三次革命。科学中的混沌概念不同于古典哲学和日常语言中的理解,简单地说,混沌是一种确定系统中出现的无规则的运动。混沌理论所研究的是非线性动力学混沌,目的是要揭示貌似随机的现象背后可能隐藏的简单规律,以求发现一大类复杂问题普遍遵循的共同规律。
1963年,Lorenz在《大气科学》杂志上发表了“决定性的非周期流”一文,指出在气候不能精确重演与长期天气预报者无能为力之间必然存在着一种联系,这就是非周期与不可预见性之间的联系。他还发现了混沌现象“对初始条件的极端敏感性” 。这可以生动的用“蝴蝶效应”来比喻:在做气象预报时,只要一只蝴蝶扇一下翅膀,这一扰动,就会在很远的另一个地方造成非常大的差异,将使长时间的预测无法进行。
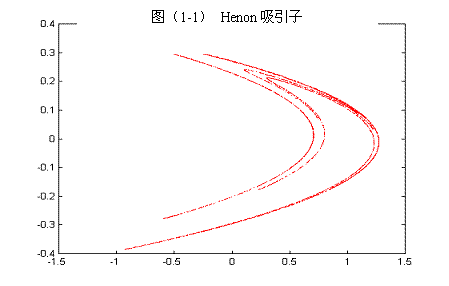
在60年代研究的基础上,混沌学的研究开始进入高潮。1971年,科学家在耗散系统中正式的引入了奇异吸引子的概念(如Henon吸引子[见图(1-1)]、Lorenz吸引子[见图(2-2)]。1975年,J.York和T.Y lie提出了混沌的科学概念。整个70年代中期,人们不但在理论上对混沌做更深层次的研究,而且努力在实验室中找寻奇异吸引子。J.York在他的著名论文“周期3意味着混沌”中,指出:在任何一维系统中,只要出现周期3,则该系统也能出现其他长度的周期,也能呈现完全的混沌。
在确定性的系统中发现混沌,改变了人们过去一直认为宇宙是一个可以预测的系统的看法。用决定论的方程,找不到稳定的模式,得到的却是随机的结果,彻底打破了拉普拉斯决定论式的可预测性的幻想。但人们同时发现到过去许多曾被认为是噪声的信号,其实是一些简单的规则生成的。这些包含内在规则的“噪声”不同于真正的噪声,它们的这种规则是完全可以应用的。
|
 |
对于什么是混沌,目前科学上还没有确切的定义,但随着研究的深入,混沌的一系列特点和本质的被揭示,对混沌完整的、具有实质性意义的确切定义将会产生。目前人们把混沌看成是一种无周期的有序。它包括如下特征:
1.混沌具有内在的确定性,它虽然貌似噪声,但不同于噪声,系统是由完全确定的方程描述的,无需附加任何随机因数,但系统仍会表现出类似随机性的行为;
2.混沌具有分形的性质,前面提到的lorenz吸引子,Henon吸引子都具有分形的结构;
3.混沌具有标度不变性,是一种无周期的有序。在由分岔导致混沌的过程中,还遵从Feigenbaum常数系。
4.混沌现象还具有对初始条件的敏感依赖性。只要初始条件稍有偏差或微小的扰动,则会使得系统的最终状态出现巨大的差异。因此混沌系统的长期演化行为是不可预测的。
检测实际系统中存在混沌现象的意义
传统上,人们把信号分为两大类:
l 确定性信号 这种信号所有时刻的波形都是确定的;
l 随机过程 它的波形由概率分布确定。
|
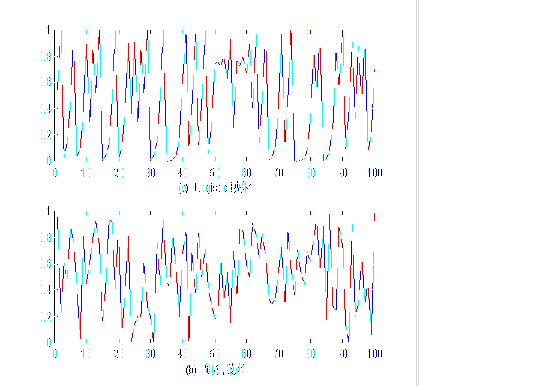 |
然而,这样的分类忽略了另一类极为重要的信号——混沌信号。混沌信号的波形是非常不规则的,表面上看来就象噪声,但实际上它却是由确定性的规则所产生的,这种规则有时是很简单的。正是这种简单的规则产生出复杂的波形激发了人们对它极大的兴趣。在图(1-2)中,我们向大家展示了由Logistic映射所生成的混沌信号与白噪声信号,从表面上我们是无法判断出噪声与混沌的。让人兴奋的是:实践证明,在大量的物理系统和自然系统中都存在着混沌信号!虽然,混沌现象的出现使我们无法对系统的长期行为进行预测,但是我们完全可以利用混沌的规律对系统进行短期的行为预测,这样比传统的统计学方法更加有效。
混沌学在工程中的应用可以分为两大类:
(1)合成混沌信号: 生成类似噪声的混沌信号
(2)分析混沌信号: 从某种现象中检测混沌信号是否存在。
在本文中,我们将主要讨论第二个话题。检测到混沌现象的存在,对我们更深刻的认识系统的特征是极为有利的。在大多数情况下,当我们确认系统中存在混沌时,我们可以利用混沌学的原理,将混沌信号从有用的信号中滤除,从而达到改善信噪比的结果,而这用传统的滤波方法有时或许是无效的。
检测混沌现象的几种方法
天然存在的系统(物理系统、化学系统或生物系统)能呈现混沌,这一点目前已得到普遍共识,并引起了许多学者在实验室里或在自然状况下对混沌识别进行尝试。然而在实验系统里,噪声会与决定系统演化的内在方程所支配的动力学特性发生相互作用,故实验系统肯定会有随机输入,从而给混沌的识别带来了许多困难。下面我们简要的介绍现今用来识别混沌的几种不同的方法。
功率谱
最为人们所熟识且应用最多的一种表征复杂时间序列特性的统计量是功率谱(power spectrum),它把复杂的时间序列分解成不同频率的正弦振荡的叠加。在给定频率处的功率谱值与频率的正弦波系数的平方成正比。典型的功率谱由一个或多个尖峰,它们对应于信号中出现的主要频率。除这些主峰外,其他频率也可能出现,不过幅度较低,而且功率谱通常分布在一个宽频带上。
宽频带功率谱(多半具有叠加尖峰)往往与混沌动态相联系。但不幸的是,“噪声”也与宽带谱密切相关,因而出现宽带谱并不足以确认与噪声相对的混沌。
相空间重构
混沌的产生是系统整体稳定性和局部不稳定性共同作用的结果,局部的不稳定性使它具有对初值的敏感性,而整体的稳定性则使它在相空间(又称状态空间)表现出一定的分形结构,这种结构被称为混沌吸引子。正是这种精密的吸引子结构,使我们可以利用它来达到分辨噪声与混沌的目的,因为真正的噪声在相空间中仍然表现出一团糟的情况。相空间重构技术是一种简单而实用的技术,但它依然有着极大的局限性。这是因为使用相空间技术来观察吸引子的结构,依靠的是人眼的辨别,当吸引子的维数高于三维时,我们将束手无策。另外,并非所有的混沌现象都存在着混沌吸引子(如Logist映射)。
李雅谱诺夫指数和维数
有关非线性动力学的研究工作已提出了一些定量刻划复杂动力学性态的量度。其中两个最常用的量是李雅谱诺夫指数(Lyapunov Exponent)和维数(Dimension),它们分别量度动力学性态的规则性程度和几何结构。李雅谱诺夫指数描述了系统轨迹收敛或发散的比率,当一个系统中同时存在正的和负的李雅谱诺夫指数时,便意味着混沌的存在。事实上李雅谱诺夫指数的重要作用之一就是判断系统的混沌行为。我们这里的维数是指的混沌吸引子所具有的分数维维数。在相空间中维数反映描述了在相空间中运动所需要的不多不少的变量个数,而在吸引子中维数则说明了刻画该吸引子所必需的信息量。
Trackback: http://tb.blog.csdn.net/TrackBack.aspx?PostId=630696