最大公约数问题
解法一
早在公元前300年,欧几里德就在《几何原本》中给出了高效的辗转相除法。欧几里得辗转相除法是现在算法的鼻祖。
算法思路(伪代码)
function gcd (a, b) while b ≠ 0 t = b b = a mod b //取余 a = t return a
算法证明
1. 两个数a、b,用a除以b,得 a = bq + r(q是商 r是余数)。若 r等于0,则b为最大公约数,否则,接着往下走
2. 证明一点:任何a和b的公约数都是r的公约数。
证明:假设d为a、b的公约数,则a = md b = nd.
r = a - bq = md - ndb = (m - nb)d. 得证
3. 对于所有的d,这都是正确的,因此a、b的公约数也即b、r的公约数。a、b的最大公约数也即b、r的最大公约数。
这样一直重复2 3过程,直到r=0。则b、r的最大公约数为b。这样得求。
例子说明
12 和 8的最大公约数:
b != 0
a = 12, b = 8 tmp = b = 8 b = a % b = 12 % 8 = 4 a = tmp = 8
b != 0 tmp = b = 4 b = a % b = 0 a = tmp = 4 最大公约数为4
程序实现
迭代思路
#include <stdio.h> int gcd(int a, int b) { int tmp; while (b != 0) { tmp = b; b = a % b; a = tmp; } return a; } int main() { printf("%d\n", gcd(12, 8)); return 0; }
递归思路
#include <stdio.h> int gcd(int a, int b) { return (!y) ? x : gcd(b, a % b); } int main() { printf("%d\n", gcd(12, 8)); return 0; }
瑕疵:用到了取模运算,对于大整数而言,取模运算是非常昂贵的开销,成为了该算法的瓶颈。
解法二
类似于欧几里德辗转相除法,两个数的公约数必然是两者之差的公约数(a = md, b = nd, a - b = (m-n)*d),因此f(a,b) = f(b, a-b),这里注意前者大于后者,否则,把两者换过来。
示例
f(42,30)=f(30,12)=f(12,18)=f(18,12)=f(12,6)=f(6,6)=f(6,0), 结果为6
代码
#include <iostream> using namespace std; int gcd(int m, int n) { if(n == 0) return m; if(m < n) return gcd(n, m); else return gcd(n, m-n); } int main() { cout << "42, 30:" << gcd(42, 30) << endl; return 0; }
结果
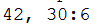
瑕疵:该方法免去了大整数除法的繁琐,但是新的不足之处在于:遇到一大一小,相差悬殊的情况(例如:(200000000, 1))
解法三
分析公约数特点:对于x和y来说(k为素数)
如果x = k * x1, y = k * y1,那么gcd(x,y)=gcd(x1,y1)*k
如果x = k * x1, y不能被k整除,那么gcd(x,y)=gcd(x1,y)
如果x不能被k整除 y = k * y1,那么gcd(x,y)=gcd(x,y1)
代码
#include <iostream> using namespace std; int gcd(int m, int n) { cout << "m, n:" << m << " " << n << endl; if(n == 0) return m; if(m < n) return gcd(n, m); else { if(m % 2 == 0) { if(n % 2 == 0) return (gcd(m >> 1, n >> 1) << 2); else return gcd(m >> 1, n); } else { if(n % 2 == 0) return gcd(m , n >> 1); else return gcd(n, m - n); } } } int main() { cout << "20000, 1000:" << gcd(20000, 1000) << endl; return 0; }
结果
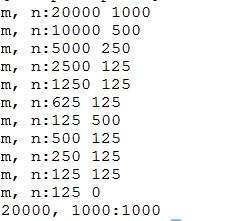
评述:解法一瓶颈在于计算大整数除法,解法二瓶颈在于有时迭代次数太多。解法三充分综合了一二的优点。另外解法三选取2作为素数,通过移位方便的进行乘除,避免了一定的大整数乘除法。
参考:《编程之美》2.7