局部性原理浅析——良好代码的基本素质
开篇
一个优秀的程序、优美的代码,一般都具有良好的局部性。简洁、高效是每个程序员的追求。了解程序的局部性,能编写出更高效的代码。
因为有良好局部性的程序能更好的利用缓存。不过这方面的只是将在以后的文章中介绍。
这篇文章就简单的介绍以下程序的局部性原理。
什么是局部性
局部性通常有两种形式:
时间局部性(temporal locality)
时间局部性指的是:被引用过一次的存储器位置在未来会被多次引用(通常在循环中)。
空间局部性(spatial locality)
如果一个存储器的位置被引用,那么将来他附近的位置也会被引用。
(这样说过于理论了些,在下面的论述中会有例子说明)
数据引用局部性
例子是最好说明问题的途径~
看图a)中的 for 循环,可以判断:循环中的 sum 有良好的时间局部性。因为在for循环结束之前,每次执行循环体都有对 sum 的访问。
而 sum 没有空间局部性。因为sum 是标量(也就是说通过 sum 这个地址(可认为是基址,只能得到一个值)
对于循环体中的 v 则有良好的空间局部性。可以看到 图 b) 中,向量 v 是按顺序存储的(在实际中多数情况也按顺序存储)。
每次访问 v[i]总是在 v[i-1] 的下一个位置。而 v 没有空间局部性。因为每个元素只被访问一次。
步长
向上面例子中按顺序、连续的对 v 的引用,我们称为步长为1的引用模式。同理,在一个连续的向量中,每隔k个元素对向量进行访问,称为步长为k的引用。一般来说,随着步长的增加,空间局部性会下降。
对于多维数组而言,步长对空间局部性的影响显得尤为重要。
考虑上面的例子,是对一个二维数组的求和。
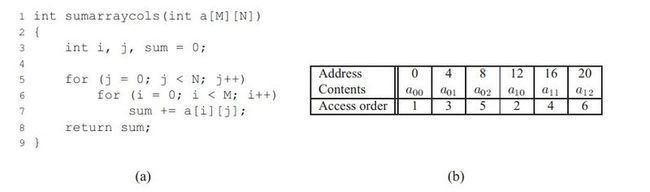
可以看到,for循环体中,是以行序为主序对元素进行遍历。也就是说内层循环先访问第一行的元素,然后第二行。。。
图 b)中是二维数组存储情况。可以看出,在存储器中也是按照行序为主序来进行存储的。也就是说先存储第一行,然后第二行。。。
现在我们已经知道了,本例中存储顺序和访问顺序一致。所以可以该程序对a[][]的引用有良好的空间局部性。
对a[][]实行的是步长为1 的引用。
继续看下面的例子:
可以看出,相对于上面的例子,该例的for 循环中交换了 索引 i j 的位置。
也就是说在对a[][]进行遍历的时候,以列序为主序。即先访问第一列,在访问第二列。。。
而b)中,对a[][]的存储仍是行序为主序。这意味着没访问一个元素,就要跳过k个存储器才能访问下一个。于是得到一个简单的结论:该例中对a[][]的访问是以步长为k 的模式(k 为每行的元素个数)没有良好的时间局部性。
通过上面的例子我们知道:在对向量的访问中,如果访问数序和存储顺序一致,并且是连续访问,那么这种访问具有良好的空间局部性。
取指令的局部性
指令存在于存储器中,cpu 要读指令就必须取出指令。所以也能评价对于取指令的局部性。
在for 循环中,循环体内的指令多次被执行,所以有良好的时间局部性。
循环体中的指令是桉顺序执行的,有良好的空间局部性(指令在存储器中是顺序存放的)。
局部性小结
评价局部性的简单原则:
1、重复引用同一个变量有良好的时间局部性
2、对于步长为k 的引用的程序,步长越小,空间局部性越小。步长为1 的引用具有良好的空间局部性。k越大,空间局部性越差。
3、对于取指令来说、循环有较好的时间和空间局部性。
后记
这篇文章只是简单的介绍了什么是局部性,局部性原理的应有,即为什么有良好局部性的程序有更好的性能,局部性和告诉缓存的关系是如何的,将在后面的文章中介绍。这篇文章且当作后文的铺垫吧。
本人认知有限,如上述文章有不足之处欢迎指正交流。
参看资料:computer systems
如有转载请注明出处:http://www.cnblogs.com/yanlingyin/
一条鱼、yanlingyin@ 博客园 2012-2-11
E-mail:[email protected]