简单算法汇总

最大公约数

/*
	 * 最大公约数-方法一 欧几里德算法
	 */
	public static int getD(int a, int b) {
		if (a == 0) {
			return b;
		}
		int r = b % a;
		return getD(r, a);
	}
	/*
	 * 最大公约数-方法二
	 */
	public static int getD2(int a, int b) {
		int t,r;
		if (a < b) {
			t = a;
			a = b;
			b = t;
		}
		while (b != 0) {
			r = a % b;
			a = b;
			b = r;
		}
		return a;
	}

最小公倍数

public static int getM(int a, int b) {
		int cdiv = getD(a, b);//cdiv为a，b的最大公约数
		return a * b / cdiv;
	}

二分查找

public static int rank(int key, int[] a) {
        Arrays.sort(a);//先对数组排序
        int lo = 0;
        int hi = a.length - 1;
        while (lo <= hi) {
            int mid = lo + (hi - lo) / 2;
            if      (key < a[mid]) hi = mid - 1;
            else if (key > a[mid]) lo = mid + 1;
            else return mid;
        }
        return -1;
    }

递归法

public static int rank(int key, int[] a) {
		return rank(key, a, 0, a.length - 1);
	}

	public static int rank(int key, int[] a, int lo, int hi) { // 如果key存在于a[]中，它的索引不会小于lo且不会大于hi
		if (lo > hi)
			return -1;
		int mid = lo + (hi - lo) / 2;
		if (key < a[mid])
			return rank(key, a, lo, mid - 1);
		else if (key > a[mid])
			return rank(key, a, mid + 1, hi);
		else
			return mid;
	}

两个方阵相乘

public static double[][] Multi(double[][] a, double[][] b) {
		int N = a.length;
		double[][] c = new double[N][N];
		for (int i = 0; i < N; i++)
			for (int j = 0; j < N; j++) { // 计算行i 和列j 的点乘
				for (int k = 0; k < N; k++)
					c[i][j] += a[i][k] * b[k][j];
			}
		return c;
	}

判断是否为素数

public static boolean isPrime(int N) {
		if (N < 2)
			return false;
		for (int i = 2; i * i <= N; i++)
			if (N % i == 0)
				return false;
		return true;
	}

计算平方根(牛顿迭代法)

public static double sqrt(double c) {
		if (c < 0)
			return Double.NaN;
		double err = 1e-15;
		double t = c;
		while (Math.abs(t - c / t) > err * t)
			t = (c / t + t) / 2.0;
		return t;
	}

选择排序

public class Selection {
	public static void sort(Comparable[] a) { // 将a[]按升序排列
		int N = a.length; // 数组长度
		for (int i = 0; i < N; i++) { // 将a[i]和a[i+1..N]中最小的元素交换
			int min = i; // 最小元素的索引
			for (int j = i + 1; j < N; j++)
				if (less(a[j], a[min]))
					min = j;
			exch(a, i, min);
		}
	}

	private static boolean less(Comparable v, Comparable w) {
		return v.compareTo(w) < 0;
	}

	private static void exch(Comparable[] a, int i, int j) {
		Comparable t = a[i];
		a[i] = a[j];
		a[j] = t;
	}

	private static void show(Comparable[] a) { // 在单行中打印数组
		for (int i = 0; i < a.length; i++)
			StdOut.print(a[i] + " ");
		StdOut.println();
	}

	public static boolean isSorted(Comparable[] a) { // 测试数组元素是否有序
		for (int i = 1; i < a.length; i++)
			if (less(a[i], a[i - 1]))
				return false;
		return true;
	}

	public static void main(String[] args) { 
		String[] a = {"12","2","3","1"};
		sort(a);
		assert isSorted(a);
		show(a);
	}
}

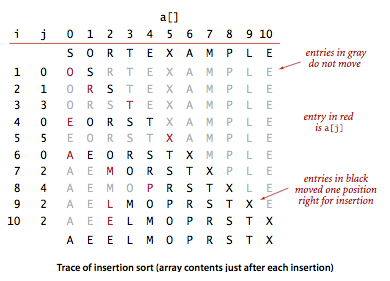
插入排序

public static void sort(Comparable[] a) {
        int N = a.length;
        for (int i = 0; i < N; i++) {
            for (int j = i; j > 0 && less(a[j], a[j-1]); j--) {//less方法和exch方法见选择排序
                exch(a, j, j-1);
            }
        }
    }

希尔排序

public static void sort(Comparable[] a) { // 将a[]按升序排列
			int N = a.length;
			int h = 1;
			while (h < N / 3)
				h = 3 * h + 1; // 1, 4, 13, 40, 121, 364, 1093, ...
			while (h >= 1) { // 将数组变为h有序
				for (int i = h; i < N; i++) { // 将a[i]插入到a[i-h], a[i-2*h], a[i-3*h]... 之中
					for (int j = i; j >= h && less(a[j], a[j - h]); j -= h)
						exch(a, j, j - h);
				}
				h = h / 3;
			}
		}