通过Scala理解什么是Monad

什么是Monad?

trait Monad[+T] {  
    def flatMap[U]( f : (T) => Monad[U] ) : Monad[U]  
    def unit(value : B) : Monad[B]
}

Monads 就是一个values的容器，并且这个“容器”必须有一个flatMap和一个unit(v)操作. 

flatMap 将monad中的一个值转换为仍在相同monad类型中的另外一个值。

unit(v), 用来包装一个values。比如Some(v)，Success(r)， List(v) 

所有monads都可以直接实现flatMap, 但是每个具体的monad必须自己实现unit(v). 在scala里，一般通过构造函数或伴生对象的apply方法来实现。

至于常用的map方法，其实只是flatMap的一个特殊形式，所以map方法不是monad所必须的：

def map[U](f : (T) => U) : Monad[U] = flatMap(v => unit(f(v)))

为什么要Monad？

（1）解决结果的不确定性问题

如果我们有一连串的操作，但是这些操作的结果是不确定的（可能得到某值，也可能抛出异常或一个非法值），当我们要把多个操作连在一起调用的时候，我们必须判断每个函数的结果是否合法，只有合法的情况下才能继续调用下一个操作，但这不是我们想要的。我们总是想尽可能的推迟知道有异常发生，而像一切都正常那样连续调用一系列操作。

比如：

val result: Try[Int] = for (
    v <- Try("5".toInt);
    k <- Try("6a".toInt);
    z <- Try("9".toInt)
  ) yield( v + k + z)

其中某一步可能会异常，但是直到必须去看这个“薛定谔的猫”之前，我们并不想关心这件事。Monad模式可以帮助我们实现这个效果。

（2）解决副作用的问题

另外一个真实世界中无法用函数式完美解决的问题是IO操作，因为IO无论如何总要伴随状态的产生或变化(也就是副作用)。

Monad来历

1990 -一个由Simon Peyton-Jones、Paul Hudak、Philip Wadler、Ashton Kutcher和善待动物组织（PETA）
组成的委员会创造了Haskell，一种纯函数式的、非严求值的语言。
Haskell由于使用了Monad这种较费解的概念来控制副作用而遭到了一些批评意见。
Wadler试图平息这些质疑，他解释说：
“一个单子（Monad）说白了不过就是自函子范畴上的一个幺半群而已，这有什么难以理解的？”

什么是幺半群？

群

G为非空集合，如果在G上定义的二元运算 *，满足

 

（1）封闭性（Closure）：对于任意a，b∈G，有a*b∈G

（2）结合律（Associativity）：对于任意a，b，c∈G，有（a*b）*c=a*（b*c）

（3）幺元 （Identity）：存在幺元e，使得对于任意a∈G，e*a=a*e=a

（4）逆元：对于任意a∈G，存在逆元a^-1，使得a^-1*a=a*a^-1=e

 

则称（G，*）是群，简称G是群。

半群(semigroup)

如果仅满足封闭性和结合律，则称G是一个半群（Semigroup）

幺半群(monoid)

如果仅满足封闭性、结合律并且有幺元，则称G是一个含幺半群（Monoid）。

这些数学概念和Monad实现的对应关系

trait Monad[+T] 就等于一个含幺半群G

def flatMap[U]( f : (T) => Monad[U] ) : Monad[U] 就等于是其中的二元运算 *，满足封闭性和结合律

def unit(value : B) : Monad[B] 就等于是幺元（Identity)，对于任意a∈G，满足e*a=a*e=a

所以对于一个Monad，他满足半群应满足的规则：

（1）结合律/封闭性

monad.flatMap(f).flatMap(g) == monad.flatMap(v => f(v).flatMap(g)) // associativity

实例：

"be associative" in {
  val multiplier : Int => Option[Int] = v => Some(v * v)
  val divider : Int => Option[Int] = v => Some(v/2)  
  val original = Some(10)  
  original.flatMap(multiplier).flatMap(divider) === 
     original.flatMap(v => multiplier(v).flatMap(divider))
}

（2）左幺元

unit(x).flatMap(f) == f(x)

实例：

"be left unit" in {  val multiplier : Int => Option[Int] = v => Some(v * v)  val item = Some(10).flatMap(multiplier)  item === multiplier(10)}

（3）右幺元

monad.flatMap(unit) == monad

实例：

"be right unit" in {
  val value = Some(50).flatMap(v => Some(v))  
  value === Some(50)
}

什么是范畴？

范畴可简单理解为高阶类型（如List[T+]），即范畴是一组类型的集合。

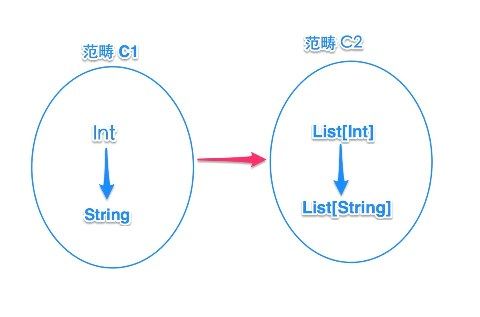
假设这里有两个范畴：范畴C1 里面有类型String 和类型 Int；范畴C2 里面有 List[String] 和List[Int]

对于”范畴C2″，它的所有类型都是List[T]的特定类型，这个范畴就可以抽象为List高阶类型。

那对于”范畴C1″呢？它又怎么抽象？其实，”范畴C1″的抽象类型可以看做是一个Identity类型构造器，它与任何参数类型作用构造出的类型就是参数类型：scala> type Id[T] = T

什么是自函子？

1. 什么是函子(Functor)？

函数(function)表达的映射关系在类型上体现在特定类型(proper type)之间的映射

函子(functor) 则是体现在高阶类型(确切的说是范畴)之间的映射

举例来说：

// 函数， Int => String
def foo(i:Int): String = i.toString

// 函子， List[T] => Set[T] 
def baz[T](l:List[T]): Set[T] = l.toSet

2. 自函子(Endofunctor)是什么？

自函数是把一个类型映射到自身类型，比如Int=>Int, String=>String 等

自函子就是一个将范畴映射到自身的函子 (A functor that maps a category to itself)

3. flatMap就是一个自函子

def flatMap[U]( f : (T) => Monad[U] ) : Monad[U]

Monad[T+]中的flatMap，就是将Monad[T+]范畴映射到Monad[U]上的自函子！（Monad[U]其实也就是Monad[T+])