NoSQL–Theory–Paxos

锁一直都是解决并发问题的良药。多线程环境中我们经常使用互斥量、信号量，在分布式环境中由于锁没有Master，并且分布式系统必定存在失效问题，我们不能用传统的同步互斥机制来解决分布式系统的并发问题。

Paxos算法是为了解决在分布式系统中，多个进程就有关某一个值达成一致决议的算法，即一种一致性算法(Consensus Algorithm)。Google的分布式锁Chubby和Yahoo的Zookeeper的实现中都采用了此算法思想。有关Paxos发布的背后的事情还挺有趣的，Paxos从提出到发布用了9年，《The Part-Time Parliament》中Lamport虚拟了一个希腊的城邦Paxos，用该城邦的人如何就一条法令达到一致来描述了整个算法，文章开始评审的时候就被建议换种描述方式，Lamport坚持自己的幽默感。但计算机界的人很多都缺少幽默感，Lamport就在2001年写了一篇相对简短的《paxox made simple》。

Paxos算法将分布式系统的进程划分为三种角色，分别为Proposer（提出者）, Acceptor（批准者）以及Learner（接受者），其中只有Proposer和Acceptor参加决议过程，Learner只是了解决议被批准以后系统具体选择的决议值。整个算法采用基于消息的传递模型，假设整个系统是消息异步，并且没有拜占庭失效问题(non-Byzantine model)，就是整个系统中的消息可以延迟到达，可以重复发送甚至可以丢失，但不能被篡改，允许系统中的节点失效和重启，但需要这些节点在失效到重启之间具有永久性存储介质用以记录信息[注1]。

Paxos算法假设：

1. Proposer（提出者）, Acceptor（批准者）以及Learner（接受者）以任意的速度操作，可能会因为停机而失效，可能会重启。因为任一个代理都可能会在决议被选择后停机再重启，因此解决方案要求代理必须能够记忆某些信息，从而能在重启后重新载入。

2. 消息传送速度不可预测，可能会重复或丢失，但是内容不会损坏（non-Byzantine model）。

如果系统现在只有一个Acceptor（批准者），Proposer（提出者）发送议案到这个Acceptor。Acceptor选择议案就非常简单，但存在单点故障。因此选择多个Acceptor，Proposer向这组Acceptor提交议案，当足够多的Acceptor接受按议案时，决议就被接受了（议案是一个{编号，决议}对）。假设没有失败或者消息丢失，即使仅有一个Proposer提出了一个决议，我们也希望能选择一个决议。这就导出了下面的需求：

P1. Acceptor必须批准它接收到的第一个决议。

这会产生一个问题，如果同时可能有几个Proposer提出了几个不同的决议，从而导致每个Acceptor都批准了一个决议，但是没有一个决议被多数派批准。一个决议要经过多数派的批准才能被选择，这个需求和P1暗示了Acceptor必须能够批准多个议案。这就就是为什么需要在每个议案中分配一个编号来记录不同的议案（议案是一个{编号，决议}对）。为避免混淆，我们要求议案的编号是唯一的。如何产生唯一的编号呢？在《Paxos made simple》中提到的是让所有的Proposer都从不相交的数据集合中进行选择，例如系统有5个Proposer，则可为每一个Proposer分配一个标识j(0~4)，则每一个proposer每次提出决议的编号可以为5*i + j(i可以用来表示提出议案的次数)。

P2. 如果一个议案{n, v}被选择，那么所有被选择的议案（编号更高）包含的决议都是v。

因为编号是全序的，P2保证了“只有一个决议被选择”这一关键安全属性。议案必须至少被一个Acceptor批准才可能被选择。因此只要满足下面的条件，就可以满足P2:

P2A. 如果一个议案{n, v}被选择，那么任何Acceptor批准的议案（编号更高）包含的决议都是v。

我们依然保证P1来确认选择了某些议案。因为通信是异步的，在特殊情况下，某些Acceptor c没有接收到过任何议案，它们可能会批准一个议案。设想一个新的Proposer“醒来”并提出了一个更高编号的议案（包含不同的决议）。根据P1的要求，c应该批准这个议案，但是这违反了P2A。为了同时保证P1和P2A，我们需要增强P2A：

P2B. 如果一个议案{n, v}被选择，那么此后，任何Proposer提出的议案（编号更高）包含的决议都是v。
因为一个议案必须在被Proposer提出后才能被Acceptor批准，因此P2B包含了P2A，进而包含了P2。
如何才能满足P2B呢？让我们来考虑如何证明它是成立的。我们假设某个议案{m, v}被选择，然后证明任何编号n>m的议案的决议都是v。

对n归纳可以简化证明，根据条件：每个提出的议案（编号从m到n-1）的决议都是v，我们可以证明编号为n的议案的决议是v。对于选择的议案（编号为m），必定存在一个集合C（Acceptor的多数派），C中的每个Acceptor都批准了该议案。结合归纳假设，m被选择这一前提意味着：C中的每个Acceptor都批准了一个编号在m到n-1范围内的议案，并且议案的决议为v。
因为任何由多数派组成的集合S都至少包含C中的一个成员，我们可以得出结论：如果下面的不变性成立，那么编号为n的议案的决议就是v：

P2C. 对于任意的v和n，如果议案{n, v}被提出，那么存在一个由Acceptor的多数派组成的集合S，或者

a) S中没有Acceptor批准过编号小于n的议案，或者

b)在S中的任何Acceptor批准的所有议案（编号小于n）中，v是编号最大的议案的决议。

通过保持P2C，我们就能满足P2B。

为了保持不变性P2C，准备提出议案（编号为n）的Proposer必须知道所有编号小于n的议案中编号最大的那个，如果存在的话，它已经或将要被Acceptor的某个多数派批准。获取已经批准的议案是简单的，但是预知将来可能批准的议案是困难的。Proposer并不做预测，而是假定不会有这样的情况。也就是说，Proposer要求Acceptor不能批准任何编号小于n的议案。这引出了下面提出议案的两阶段提交算法：

1. Proposer选择一个新编号n，向某个Acceptor集合中的所有成员发送请求，（Prepare请求阶段，n是Prepare请求的编号，也是下面Accept请求的议案编号）并要求回应：
a) 一个永不批准编号小于n的议案的承诺，以及
b) 在它已经批准的所有编号小于n的议案中，编号最大的议案，如果存在的话。

我把这样的请求称为Prepare请求n。

2 如果Proposer收到了多数Acceptor的回应，那么它就可以提出议案{n, v}，其中v是所有回应中编号最高的议案的决议，或者是Proposer选择的任意值，如果Acceptor们回应说还没有批准过议案。

一个Proposer向一个Acceptor集合发送已经被批准的议案（不一定是回应Proposer初始请求的Acceptor集合），我们称之为Accept请求。

我们已经描述了Proposer的算法。那么Acceptor呢？它可以接收两种来自Proposer的请求： Prepare请求和Accept请求。Acceptor可以忽略任何请求，而不用担心安全性。因此，我们只需要描述它需要回应请求的情况。任何时候它都可以回应Prepare请求，它可以回应Accept请求，并批准议案，当且仅当

P1A. Acceptor可以批准一个编号为n的议案，当且仅当它没有回应过一个编号大于n的Prepare请求。

P1A蕴含了P1。

现在我们得到了一个完整的决议选择算法，并满足我们要求的安全属性——假设议案编号唯一。通过一些简单优化就能得到最终算法。

假设一个Acceptor接收到一个编号为n的Prepare请求，但是它已经回应了一个编号大于n的Prepare请求。于是Acceptor就没有必要回应这个Prepare请求了，因为它不会批准这个编号为n的议案。它还可以忽略已经批准过的议案的Prepare请求。

有了这个优化，Acceptor只需要保存它已经批准的最高编号的议案（包括编号和决议），以及它已经回应的所有Prepare请求的最高编号。因为任何情况下，都需要保证P2C，Acceptor必须记住这些信息，包括失效并重启之后。注意，Proposer可以随意的抛弃一个议案——只要它永远不会使用相同的编号来提出另一个议案。
结合Proposer和Acceptor的行为，我们将把算法可以分为两个阶段[注2]来执行。

阶段1.
a) Proposer选择一个议案编号n，向Acceptor的多数派发送编号也为n的Prepare请求。
b) Acceptor：如果接收到的Prepare请求的编号n大于它已经回应的任何Prepare请求，它就回应已经批准的编号最高的议案（如果有的话），并承诺不再回应任何编号小于n的议案；

阶段2.
a) Proposer：如果收到了多数Acceptor对Prepare请求（编号为n）的回应，它就向这些Acceptor发送议案{n, v}的Accept请求，其中v是所有回应中编号最高的议案的决议，或者是Proposer选择的任意值，如果回应说还没有议案。
b) Acceptor：如果收到了议案{n, v}的Accept请求，它就批准该议案，除非它已经回应了一个编号大于n的议案。

Proposer可以提出多个议案，只要它遵循上面的算法。它可以在任何时刻放弃一个议案。（这不会破坏正确性，即使在议案被放弃后，议案的请求或者回应消息才到达目标）如果其它的Proposer已经开始提出更高编号的议案，那么最好能放弃当前的议案。因此，如果Acceptor忽略一个Prepare或者Accept请求（因为已经收到了更高编号的Prepare请求），它应该告知Proposer放弃议案。这是一个性能优化，而不影响正确性。

Learner必须找到一个被多数Acceptor批准的议案，才能知道一个决议被选择了。一个显而易见的算法就是，让每个Acceptor在批准议案时通知所有的Learner。于是Learner可以尽快知道选择的决议，但是要求每个Acceptor通知每个Learner需要的消息个数等于Learner数和Acceptor数的乘积。

基于非拜占庭假设，一个Learner可以从另一个Learner得知被选择的决议。我们可以让Acceptor将批准情况回应给一个主Learner，它再把被选择的决议通知给其它的Learner。这增加了一次额外的消息传递，也不可靠，因为主Learner可能会失效，但是要求的消息个数仅是Learner数和Acceptor数的总和。

更一般的，可以有多个主Learner，每个都能通知其它所有的Acceptor。主Learner越多越可靠，但是通信代价会增加。

由于消息丢失，可能没有Learner知道选择了一个决议。Learner可以向Acceptor询问批准的议案，但是由于Acceptor的失效，可能难以得知多数派是否批准了一个议案。这样，Learner只能在新的议案被选择时才能知道Acceptor选择的决议。如果Learner需要知道是否已经选择了一个决议，它可以让proposer根据上面的算法提出一个议案,因为提出请求就有回应，并且新的提案的决议就是当前选择的决议。

很容易构造这样一个场景，两个Proposer轮流提出一系列编号递增的议案，但是都没有被选择。Propoer p选择议案的编号为n1，并结束阶段1。接着，另外一个Proposer q选择了议案编号n2>n1，并结束阶段1。于是p在阶段2的Accept请求将被忽略，因为acceptor已经承诺不再批准编号小于n2的议案。于是p再回到阶段1并选择了编号n3 > n2，这又导致q第二阶段的accept请求被忽略，…这将导致活锁，达不了一致。

为了保证流程，必须选择一个主Proposer，只有主Proposer才能提出议案。如果主Proposer和多数Acceptor成功通信，并提出一个编号更高的议案，议案将被批准。如果它得知已经有编号更高的议案，它将放弃当前的议案，并最终能选择一个足够大的编号。如果系统中有足够的组件能正常工作，通过选择一个主Proposer，系统就能保持响应。Fischer、Lynch和Patterson的著名结论表明：选择Proposer的可靠算法必须是随机的或者实时的。然而不管选择成功与否，安全性都能得到保证。

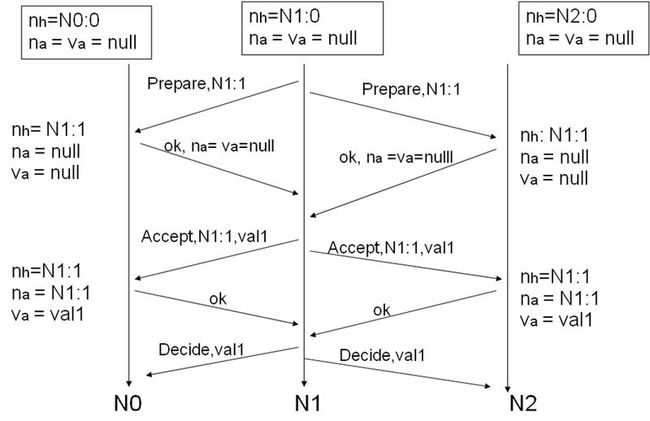
经过前面的的讨论，Paxos算法如下：

每个代理维护三个变量：na，va：编号最高的提议编号和对应接受的值；nh：见到的最大编号提议；myn：自己的提议编号。

1. 一个代理被选为Leader来做提议；

2. Leader选择一个myn，并满足myn> nh；

3. Leader向所有代理发送<prepare, myn>；

4. Acceptor代理收到<prepare, n>做如下操作：

    If n < nh

        回复 <prepare-reject>

    Else

         nh = n

         回复 <prepare-ok, na,va>

5. 如果Leader从多数Acceptor那得到prepare-ok：

    V是收到最大编号na议案的值

    If V= null表明Acceptor没有收到其他议案，Leader可以使用任意V

        发送 <accept, myn, V> 到所有代理。

    如果Leader没有收到Acceptor的prepare-ok：

        随机退步，然后重启Paxos算法。

6. Acceptor代理收到<accept, n, V>：

    If n < nh

         回复<accept-reject>

     else

         na = n; va = V; nh = n

         回复<accept-ok>

7. 如果Leader收到多数Acceptor的accept-ok

         向代理回复<decide, va>s

    否则

         随机退步，然后重启Paxos算法。

下面是一个Paxos算法实例：

注1：拜占庭模型（Byzantine model），消息可能丢失、重复或者内容损坏。换而言之，非拜占庭模型就是允许消息的丢失或者重复，但是不会出现内容损坏的情况。

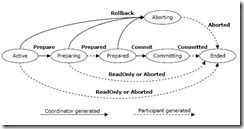
注2：两阶段提交是分布式系统的常用事务处理方法。两阶段提交的过程涉及到协调者和参与者。协调者可以看做成事务的发起者，同时也是事务的一个参与者。对于一个分布式事务来说，一个事务是涉及到多个参与者的。具体的提交过程：

第一阶段：

首先，协调者向所有参与者发送消息prepare T，询问这些参与者（包括自身），是否能够提交这个事务；参与者在接受到这个prepare T 消息以后，会根据自身的情况，进行事务的预处理，如果参与者能够提交该事务，并返回给协调者一个ready T信息，同时自身进入预提交状态状态；如果不能提交该事务，则返回一个not commit T信息给协调者；参与者能够推迟发送响应的时间，但最终还是需要发送的。

第二阶段：

协调者会收集所有参与者的意见，如果收到参与者发来的not commit T信息，则标识着该事务不能提交，协调者会向所有参与者发送一个abort T 信息，让所有参与者撤销在自身上所有的预操作；如果协调者收到所有参与者发来prepare T信息，则向所有参与者发送一个commit T信息，提交该事务。若协调者迟迟未收到某个参与者发来的信息，则认为该参与者发送了一个abort T信息，从而取消该事务的执行。参与者接收到协调者发来的abort T信息以后，参与者会终止提交；如果参与者收到的是commit T信息，则会将事务进行提交。