圆与未旋转矩形的碰撞检测(上篇)
我们以Cocos2d-x Lua脚本来说明圆与未旋转矩形的碰撞检测,原理才是重点,本文参照了两种方法。
第一种方法:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
bool
intersects(CircleType circle, RectType rect)
{
//1
circleDistance.x =
abs
(circle.x - rect.x);
circleDistance.y =
abs
(circle.y - rect.y);
//2
if
(circleDistance.x > (rect.width/2 + circle.r)) {
return
false
; }
if
(circleDistance.y > (rect.height/2 + circle.r)) {
return
false
; }
//3
if
(circleDistance.x <= (rect.width/2)) {
return
true
; }
if
(circleDistance.y <= (rect.height/2)) {
return
true
; }
//4
cornerDistance_sq = (circleDistance.x - rect.width/2)^2 +
(circleDistance.y - rect.height/2)^2;
return
(cornerDistance_sq <= (circle.r^2));
}
|
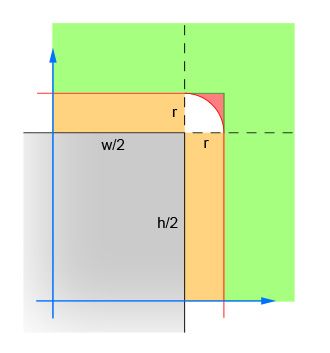
circle.x, circle.y为圆心;rect.x, rect.y为矩形的中心。如图:
代码注释:
-
第一对语句计算圆的中心到矩形中心的x与y的差值的绝对值。将四个象限重合为一个,这样就不需要计算四次。注意,这里只显示了第一象限。灰色区域代表矩形,红色边界轮廓的临界区域与矩形的距离正是一个半径的长度。圆的中心必须在这个红色十字交叉的边界处。
-
第二对语句判断圆与矩形(在任何一个方向中)之间的距离很大不会出现交叉的简单的情况。如图中绿色区域所示。
-
第三对语句判断圆与矩形(在任何一个方向中)之间的距离很小,一定会产生交叉简单的情况。如图中橘色和灰色的交叉区域。注意,必须在第二步完成之后做这一步的判断,以便更合逻辑。
-
最后两句判断圆和矩形的一角可能相交的复杂情况,计算圆心到角的距离,然后验证这个距离不超过圆的半径。若圆心在红色阴影区内,则结果返回FALSE;若圆心在白色阴影区内,则结果返回TRUE。
(翻译自:http://stackoverflow.com/questions/401847/circle-rectangle-collision-detection-intersection)
第二种方法,检测圆和矩形碰撞,要找到矩形上离圆的中心点最近的点计算
|
1
2
3
|
if
circle.x < box.x then
cx = box.x
end
|
如果圆在矩形的左边,离着圆中心点最近的矩形上的点在矩形的左边边界上
|
1
2
|
elseif circle.x > box.x + box.width then
cx = box.x + box.width
|
如果圆的中心点在矩形的右边,离着圆中心点最近的矩形上的点在矩形的右边边界上
|
1
2
|
else
cx = circle.x
|
如果圆心x既不在矩形的左边也不在右边, 那么cx就在矩形内
同理,找到Y方向上离着圆中心点最近的y偏移cy
|
1
2
3
4
5
6
7
|
if
circle_pt.y < rect.y then
cy = rect.y
elseif circle_pt.y > rect.y + rect.height then
cy = rect.y + rect.height
else
cy = circle_pt.y
end
|
最后附上Lua版的圆与矩形的碰撞,圆与圆的碰撞检测
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
--[[--
检测圆和未旋转的矩形之间的碰撞
参考:http:
//lazyfoo.net/SDL_tutorials/lesson19/index.php
~~~ lua
local intersects = circleIntersectRect(cc.p(10, 10), 50, cc.rect(20, 20, 100, 100))
~~~
param: circle_pt 圆心
param: radius 半径
param: rect 矩形 {x=0,y=0,width=100,height=100}
@see
]]
function circleIntersectRect(circle_pt, radius, rect)
local cx = nil
local cy = nil
-- Find the point on the collision box closest to the center of the circle
if
circle_pt.x < rect.x then
cx = rect.x
elseif circle_pt.x > rect.x + rect.width then
cx = rect.x + rect.width
else
cx = circle_pt.x
end
if
circle_pt.y < rect.y then
cy = rect.y
elseif circle_pt.y > rect.y + rect.height then
cy = rect.y + rect.height
else
cy = circle_pt.y
end
if
cc.pGetDistance(circle_pt, cc.p(cx, cy)) < radius then
return
true
end
return
false
end
--[[--
检测圆之间的碰撞
~~~ lua
local intersects = circleIntersects(cc.p(10, 10), 10, cc.p(20,20), 20)
~~~
@param : circle_pt_a 圆A中心
@param : radius_a 圆A半径
@param : circle_pt_b 圆B中心
@param : radius_b 圆B半径
@
return
是否碰撞
@see
]]
function circleIntersects(circle_pt_a, radius_a, circle_pt_b, radius_b)
-- If the distance between the centers of the circles is less than the sum of their radius
if
cc.pGetDistance(circle_pt_a, circle_pt_b) < (radius_a + radius_b) then
return
true
end
return
false
end
|
参考:
Circular Collision Detection
来源网址:http://blog.csdn.net/teng_ontheway/article/details/38706837