CSU 1412 Line and Circles

　　原题链接：http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1412

　　题目要求判断是否有一条直线可以穿过所有的圆。

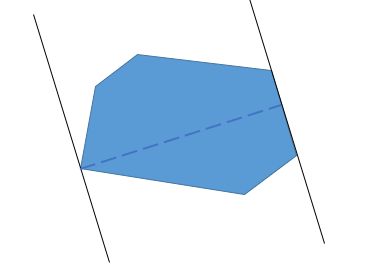
　　做法：把所有圆心做一次凸包，然后判断这个凸包是否能通过一个宽度为2*R的通道。

　　做法和求凸包直径差不多，只是判断的时候把点到两个端点的距离换成点到直线的距离。

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;

#define inf 1e20
#define eps 1e-8

const int N = 100005 ;
const double PI = 2.0*asin(1.0); //高精度求PI
struct Lpoint
{
    double x,y;
}a[N], b[N]; //点
struct Llineseg
{
    Lpoint a,b;
}; //线段
struct Ldir
{
    double dx,dy;
}; //方向向量
struct Lline
{
    Lpoint p;
    Ldir dir;
}; //直线

bool mult(Lpoint sp, Lpoint ep, Lpoint op)
{
    return (sp.x - op.x) * (ep.y - op.y)
           >= (ep.x - op.x) * (sp.y - op.y);
}

bool operator < (const Lpoint &l, const Lpoint &r)
{
    return l.y < r.y || (l.y == r.y && l.x < r.x);
}

int graham(Lpoint pnt[], int n, Lpoint res[])
{
    int i, len, top = 1;
    sort(pnt, pnt + n);
    if (n == 0) return 0;
    res[0] = pnt[0];
    if (n == 1) return 1;
    res[1] = pnt[1];
    if (n == 2) return 2;
    res[2] = pnt[2];
    for (i = 2; i < n; i++)
    {
        while (top && mult(pnt[i], res[top], res[top-1]))
            top--;
        res[++top] = pnt[i];
    }
    len = top;
    res[++top] = pnt[n - 2];
    for (i = n - 3; i >= 0; i--)
    {
        while (top!=len && mult(pnt[i], res[top], res[top-1])) top--;
        res[++top] = pnt[i];
    }
    return top; // 返回凸包中点的个数
}

void format(Lline ln, double& A, double& B, double& C)
{
    A=ln.dir.dy;
    B=-ln.dir.dx;
    C=ln.p.y*ln.dir.dx-ln.p.x*ln.dir.dy;
    
}

double p2ldis(Lpoint a, Lline ln)
{
    double A,B,C;
    format(ln,A,B,C);
    return(fabs(A*a.x+B*a.y+C)/sqrt(A*A+B*B));
}

double CPMD(Lpoint p[], int n)//ConvexPolygonMinimumDiameter
{ 
    int i, j; 
    double ans = inf, tmp;
    p[n] = p[0]; 
    Lline ln; 
    Ldir dir;
    for(i = 0, j = 1; i < n; ++i) 
    { 
        if((i+1)%n == j) j = (j + 1) % n;
        dir.dx = p[i].x - p[i+1].x;
        dir.dy = p[i].y - p[i+1].y;
        ln.dir = dir;
        ln.p = p[i];
        while((tmp = p2ldis(p[j], ln)) < (p2ldis(p[(j+1)%n], ln)))
            j = (j + 1) % n;
        ans = min(ans, tmp);
    } 
    return ans; 
} 

double dis(Lpoint u, Lpoint v)
{
    return sqrt((u.x-v.x) * (u.x-v.x) + (u.y - v.y)*(u.y - v.y));
}

int main()
{
    int n, t;
    double r;
    scanf("%d", &t); 
    while(t--)
    {
        scanf("%d%lf", &n, &r);
        for(int i = 0; i < n; i++)
            scanf("%lf%lf", &a[i].x, &a[i].y);
        int m = graham(a, n, b);
        if(m <= 2)
        {
            printf("Yes\n");
            continue;
        }
        double k = CPMD(b, m);
        if(k - 2*r < eps)
            printf("Yes\n");
        else
            printf("No\n");
    }
    return 0;
}

View Code