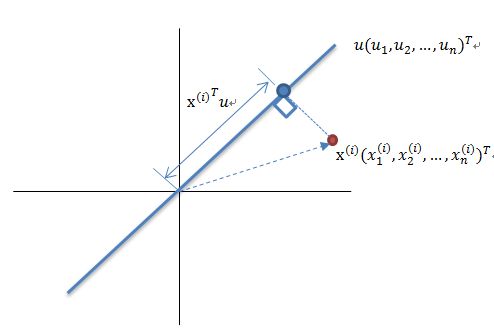
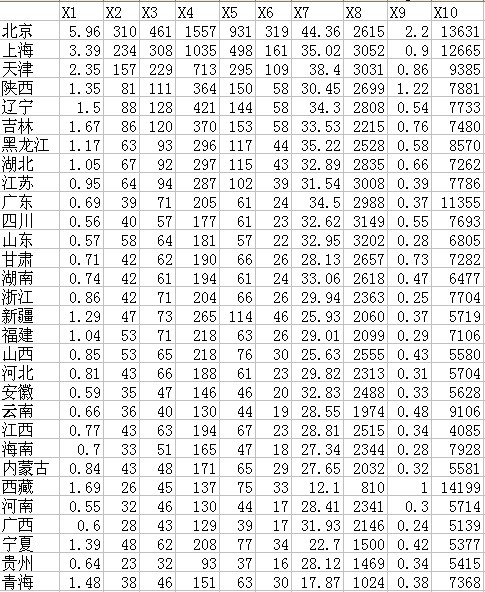
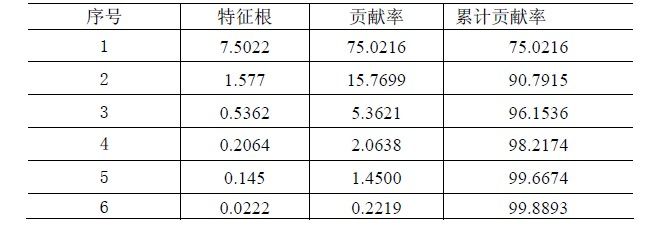
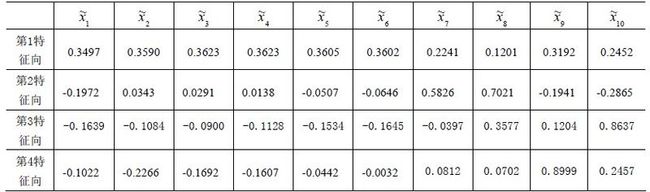
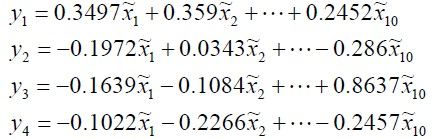- LocalDateTime 转 String
igotyback
java开发语言
importjava.time.LocalDateTime;importjava.time.format.DateTimeFormatter;publicclassMain{publicstaticvoidmain(String[]args){//获取当前时间LocalDateTimenow=LocalDateTime.now();//定义日期格式化器DateTimeFormatterformat
- mysql禁用远程登录
igotyback
mysql
去mysql库中的user表里,将host都改成localhost之后刷新权限FLUSHPRIVILEGES;
- Linux下QT开发的动态库界面弹出操作(SDL2)
13jjyao
QT类qt开发语言sdl2linux
需求:操作系统为linux,开发框架为qt,做成需带界面的qt动态库,调用方为java等非qt程序难点:调用方为java等非qt程序,也就是说调用方肯定不带QApplication::exec(),缺少了这个,QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出);这与qt调用本身qt库是有本质的区别的思路:1.调用方缺QApplication::exec(),那么我们在接口
- 每日一题——第八十三题
互联网打工人no1
C语言程序设计每日一练c语言
题目:将输入的整形数字输出,输出1990,输出"1990"#include#defineMAX_INPUT1024intmain(){intarrr_num[MAX_INPUT];intnum,i=0;printf("请输入一个数字:");scanf_s("%d",&num);while(num!=0){arrr_num[i++]=num%10;num/=10;}printf("\"");for(
- C#中使用split分割字符串
互联网打工人no1
c#
1、用字符串分隔:usingSystem.Text.RegularExpressions;stringstr="aaajsbbbjsccc";string[]sArray=Regex.Split(str,"js",RegexOptions.IgnoreCase);foreach(stringiinsArray)Response.Write(i.ToString()+"");输出结果:aaabbbc
- Goolge earth studio 进阶4——路径修改与平滑
陟彼高冈yu
Googleearthstudio进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径,所以当我们通过这个关键帧时,不是一个生硬的角度,而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄,允许我们调整路径的形状。右键单击,我们可以选择“平滑路径”,这是默认的自动平滑算法,或者我们可
- 【目标检测数据集】卡车数据集1073张VOC+YOLO格式
熬夜写代码的平头哥∰
目标检测YOLO人工智能
数据集格式:PascalVOC格式+YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数):1073标注数量(xml文件个数):1073标注数量(txt文件个数):1073标注类别数:1标注类别名称:["truck"]每个类别标注的框数:truck框数=1120总框数:1120使用标注工具:labelImg标注
- 钢筋长度超限检测检数据集VOC+YOLO格式215张1类别
futureflsl
数据集YOLO深度学习机器学习
数据集格式:PascalVOC格式+YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数):215标注数量(xml文件个数):215标注数量(txt文件个数):215标注类别数:1标注类别名称:["iron"]每个类别标注的框数:iron框数=215总框数:215使用标注工具:labelImg标注规则:对类别进
- 【PG】常见数据库、表属性设置
江无羡
数据库
PG的常见属性配置方法数据库复制、备份相关表的复制标识单表操作批量表操作链接数据库复制、备份相关表的复制标识单表操作通过ALTER语句单独更改一张表的复制标识。ALTERTABLE[tablename]REPLICAIDENTITYFULL;批量表操作通过代码块的方式,对某个schema中的所有表一起更新其复制标识。SELECTtablename,CASErelreplidentWHEN'd'TH
- 每日一题——第八十八题
互联网打工人no1
C语言程序设计每日一练c语言
题目:输入一个9位的无符号整数,判断其是否有重复数字#include#include#includeintmain(){charnum_str[10];printf("请输入一个9位数的无符号数:");scanf_s("%9d",&num_str);if(strlen(num_str)!=9){printf("输入的不是一个9位无符号整数,请重新输入");}else{if(hasDuplicate
- SpringBlade dict-biz/list 接口 SQL 注入漏洞
文章永久免费只为良心
oracle数据库
SpringBladedict-biz/list接口SQL注入漏洞POC:构造请求包查看返回包你的网址/api/blade-system/dict-biz/list?updatexml(1,concat(0x7e,md5(1),0x7e),1)=1漏洞概述在SpringBlade框架中,如果dict-biz/list接口的后台处理逻辑没有正确地对用户输入进行过滤或参数化查询(PreparedSta
- xilinx vivado PULLMODE 设置思路
坚持每天写程序
fpga开发
1.xilinx引脚分类XilinxIO的分类:以XC7A100TFGG484为例,其引脚分类如下:1.UserIO(用户IO):用户使用的普通IO1.1专用(Dedicated)IO:命名为IO_LXXY_#、IO_XX_#的引脚,有固定的特定用途,多为底层特定功能的直接实现,如差分对信号、关键控制信号等,不能随意变更。1.2多功能(Multi-Function)IO:命名为IO_LXXY_ZZ
- 自然语言处理_tf-idf
_feivirus_
算法机器学习和数学自然语言处理tf-idf逆文档频率词频
importpandasaspdimportmath1.数据预处理docA="Thecatsatonmyface"docB="Thedogsatonmybed"wordsA=docA.split("")wordsB=docB.split("")wordsSet=set(wordsA).union(set(wordsB))print(wordsSet){'on','my','face','sat',
- 第1步win10宿主机与虚拟机通过NAT共享上网互通
学习3人组
大数据大数据
VM的CentOS采用NAT共用宿主机网卡宿主机器无法连接到虚拟CentOS要实现宿主机与虚拟机通信,原理就是给宿主机的网卡配置一个与虚拟机网关相同网段的IP地址,实现可以互通。1、查看虚拟机的IP地址2、编辑虚拟机的虚拟网络的NAT和DHCP的配置,设置虚拟机的网卡选择NAT共享模式3、宿主机的IP配置,确保vnet8的IPV4属性与虚拟机在同一网段4、ping测试连通性[root@localh
- ArrayList 源码解析
程序猿进阶
Java基础ArrayListListjava面试性能优化架构设计idea
ArrayList是Java集合框架中的一个动态数组实现,提供了可变大小的数组功能。它继承自AbstractList并实现了List接口,是顺序容器,即元素存放的数据与放进去的顺序相同,允许放入null元素,底层通过数组实现。除该类未实现同步外,其余跟Vector大致相同。每个ArrayList都有一个容量capacity,表示底层数组的实际大小,容器内存储元素的个数不能多于当前容量。当向容器中添
- matlab mle 优化,MLE+: Matlab Toolbox for Integrated Modeling, Control and Optimization for Buildings...
Simon Zhong
matlabmle优化
摘要:FollowingunilateralopticnervesectioninadultPVGhoodedrat,theaxonguidancecueephrin-A2isup-regulatedincaudalbutnotrostralsuperiorcolliculus(SC)andtheEphA5receptorisdown-regulatedinaxotomisedretinalgan
- Android应用性能优化
轻口味
Android
Android手机由于其本身的后台机制和硬件特点,性能上一直被诟病,所以软件开发者对软件本身的性能优化就显得尤为重要;本文将对Android开发过程中性能优化的各个方面做一个回顾与总结。Cache优化ListView缓存:ListView中有一个回收器,Item滑出界面的时候View会回收到这里,需要显示新的Item的时候,就尽量重用回收器里面的View;每次在getView函数中inflate新
- uniapp map组件自定义markers标记点
以对_
uni-app学习记录uni-appjavascript前端
需求是根据后端返回数据在地图上显示标记点,并且根据数据状态控制标记点颜色,标记点背景通过两张图片实现控制{{item.options.labelName}}exportdefault{data(){return{storeIndex:0,locaInfo:{longitude:120.445172,latitude:36.111387},markers:[//标点列表{id:1,//标记点idin
- 基于STM32的汽车仪表显示系统:集成CAN、UART与I2C总线设计流程
极客小张
stm32汽车嵌入式硬件物联网单片机c语言
一、项目概述项目目标与用途本项目旨在设计和实现一个基于STM32微控制器的汽车仪表显示系统。该系统能够实时显示汽车的速度、转速、油量等关键信息,并通过CAN总线与其他汽车控制单元进行通信。这种仪表显示系统不仅提高了驾驶的安全性和便捷性,还能为汽车提供更智能的用户体验。技术栈关键词微控制器:STM32显示技术:TFTLCD/OLED传感器:速度传感器、温度传感器、油量传感器通信协议:CAN总线、UA
- 怎么做才能真正限制塑料袋的使用?
BalNews
Environmentalpollutionisalwaysamajorlivelihoodissue.Morethanadecadeago,ourgovernmenthadintroducedapolicyaboutrestrictionsontheuseofplasticbags,wecallitrestrictionsontheuseofplasticbags.Butmorethan10ye
- Python实现下载当前年份的谷歌影像
sand&wich
python开发语言
在GIS项目和地图应用中,获取最新的地理影像数据是非常重要的。本文将介绍如何使用Python代码从Google地图自动下载当前年份的影像数据,并将其保存为高分辨率的TIFF格式文件。这个过程涉及地理坐标转换、多线程下载和图像处理。关键功能该脚本的核心功能包括:坐标转换:支持WGS-84与WebMercator投影之间转换,以及处理中国GCJ-02偏移。自动化下载:多线程下载地图瓦片,提高效率。图像
- Vue( ElementUI入门、vue-cli安装)
m0_l5z
elementuivue.js
一.ElementUI入门目录:1.ElementUI入门1.1ElementUI简介1.2Vue+ElementUI安装1.3开发示例2.搭建nodejs环境2.1nodejs介绍2.2npm是什么2.3nodejs环境搭建2.3.1下载2.3.2解压2.3.3配置环境变量2.3.4配置npm全局模块路径和cache默认安装位置2.3.5修改npm镜像提高下载速度2.3.6验证安装结果3.运行n
- 博客网站制作教程
2401_85194651
javamaven
首先就是技术框架:后端:Java+SpringBoot数据库:MySQL前端:Vue.js数据库连接:JPA(JavaPersistenceAPI)1.项目结构blog-app/├──backend/│├──src/main/java/com/example/blogapp/││├──BlogApplication.java││├──config/│││└──DatabaseConfig.java
- 计算机毕业设计PHP仓储综合管理系统(源码+程序+VUE+lw+部署)
java毕设程序源码王哥
php课程设计vue.js
该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程。欢迎交流项目运行环境配置:phpStudy+Vscode+Mysql5.7+HBuilderX+Navicat11+Vue+Express。项目技术:原生PHP++Vue等等组成,B/S模式+Vscode管理+前后端分离等等。环境需要1.运行环境:最好是小皮phpstudy最新版,我们在这个版本上开发的。其他版本理论上也可以。2.开发
- RabbitMQ生产者重复机制与确认机制
java炒饭小能手
java-rabbitmqrabbitmqjava
重复机制生产者发送消息时,出现了网络故障,导致与MQ的连接中断。为了解决这个问题,SpringAMQP提供的消息发送时的重试机制。即:当RabbitTemplate与MQ连接超时后,多次重试。需要修该发送端模块的application.yaml文件,添加下面的内容:spring:rabbitmq:connection-timeout:1s#设置MQ的连接超时时间template:retry:ena
- 华为云分布式缓存服务DCS 8月新特性发布
华为云PaaS服务小智
华为云分布式缓存
分布式缓存服务(DistributedCacheService,简称DCS)是华为云提供的一款兼容Redis的高速内存数据处理引擎,为您提供即开即用、安全可靠、弹性扩容、便捷管理的在线分布式缓存能力,满足用户高并发及数据快速访问的业务诉求。此次为大家带来DCS8月的特性更新内容,一起来看看吧!
- 【算法练习】IDEA集成leetcode插件实现快速刷
2401_84102892
2024年程序员学习算法intellij-idealeetcode
============点击右侧边leetcode->设置->配置地址、用户名、密码、存放目录、文件模板用户名要登录后在账号信息里看模板代码1.codefilename!velocityTool.camelC
- Day_11
ROC_bird..
算法
面试题16.15.珠玑妙算-力扣(LeetCode)/***Note:Thereturnedarraymustbemalloced,assumecallercallsfree().*///下标和对应位置的值都一样,answer[0]+1,对应位置的值猜对了,但是下标不对,answer[1]+1int*masterMind(char*solution,char*guess,int*returnSiz
- leetcode中等.数组(21-40)python
九日火
pythonleetcode
80.RemoveDuplicatesfromSortedArrayII(m-21)Givenasortedarraynums,removetheduplicatesin-placesuchthatduplicatesappearedatmosttwiceandreturnthenewlength.Donotallocateextraspaceforanotherarray,youmustdoth
- 前端代码上传文件
余生逆风飞翔
前端javascript开发语言
点击上传文件import{ElNotification}from'element-plus'import{API_CONFIG}from'../config/index.js'import{UploadFilled}from'@element-plus/icons-vue'import{reactive}from'vue'import{BASE_URL}from'../config/index'i
- LeetCode[位运算] - #137 Single Number II
Cwind
javaAlgorithmLeetCode题解位运算
原题链接:#137 Single Number II
要求:
给定一个整型数组,其中除了一个元素之外,每个元素都出现三次。找出这个元素
注意:算法的时间复杂度应为O(n),最好不使用额外的内存空间
难度:中等
分析:
与#136类似,都是考察位运算。不过出现两次的可以使用异或运算的特性 n XOR n = 0, n XOR 0 = n,即某一
- 《JavaScript语言精粹》笔记
aijuans
JavaScript
0、JavaScript的简单数据类型包括数字、字符创、布尔值(true/false)、null和undefined值,其它值都是对象。
1、JavaScript只有一个数字类型,它在内部被表示为64位的浮点数。没有分离出整数,所以1和1.0的值相同。
2、NaN是一个数值,表示一个不能产生正常结果的运算结果。NaN不等于任何值,包括它本身。可以用函数isNaN(number)检测NaN,但是
- 你应该更新的Java知识之常用程序库
Kai_Ge
java
在很多人眼中,Java 已经是一门垂垂老矣的语言,但并不妨碍 Java 世界依然在前进。如果你曾离开 Java,云游于其它世界,或是每日只在遗留代码中挣扎,或许是时候抬起头,看看老 Java 中的新东西。
Guava
Guava[gwɑ:və],一句话,只要你做Java项目,就应该用Guava(Github)。
guava 是 Google 出品的一套 Java 核心库,在我看来,它甚至应该
- HttpClient
120153216
httpclient
/**
* 可以传对象的请求转发,对象已流形式放入HTTP中
*/
public static Object doPost(Map<String,Object> parmMap,String url)
{
Object object = null;
HttpClient hc = new HttpClient();
String fullURL
- Django model字段类型清单
2002wmj
django
Django 通过 models 实现数据库的创建、修改、删除等操作,本文为模型中一般常用的类型的清单,便于查询和使用: AutoField:一个自动递增的整型字段,添加记录时它会自动增长。你通常不需要直接使用这个字段;如果你不指定主键的话,系统会自动添加一个主键字段到你的model。(参阅自动主键字段) BooleanField:布尔字段,管理工具里会自动将其描述为checkbox。 Cha
- 在SQLSERVER中查找消耗CPU最多的SQL
357029540
SQL Server
返回消耗CPU数目最多的10条语句
SELECT TOP 10
total_worker_time/execution_count AS avg_cpu_cost, plan_handle,
execution_count,
(SELECT SUBSTRING(text, statement_start_of
- Myeclipse项目无法部署,Undefined exploded archive location
7454103
eclipseMyEclipse
做个备忘!
错误信息为:
Undefined exploded archive location
原因:
在工程转移过程中,导致工程的配置文件出错;
解决方法:
- GMT时间格式转换
adminjun
GMT时间转换
普通的时间转换问题我这里就不再罗嗦了,我想大家应该都会那种低级的转换问题吧,现在我向大家总结一下如何转换GMT时间格式,这种格式的转换方法网上还不是很多,所以有必要总结一下,也算给有需要的朋友一个小小的帮助啦。
1、可以使用
SimpleDateFormat SimpleDateFormat
EEE-三位星期
d-天
MMM-月
yyyy-四位年
- Oracle数据库新装连接串问题
aijuans
oracle数据库
割接新装了数据库,客户端登陆无问题,apache/cgi-bin程序有问题,sqlnet.log日志如下:
Fatal NI connect error 12170.
VERSION INFORMATION: TNS for Linux: Version 10.2.0.4.0 - Product
- 回顾java数组复制
ayaoxinchao
java数组
在写这篇文章之前,也看了一些别人写的,基本上都是大同小异。文章是对java数组复制基础知识的回顾,算是作为学习笔记,供以后自己翻阅。首先,简单想一下这个问题:为什么要复制数组?我的个人理解:在我们在利用一个数组时,在每一次使用,我们都希望它的值是初始值。这时我们就要对数组进行复制,以达到原始数组值的安全性。java数组复制大致分为3种方式:①for循环方式 ②clone方式 ③arrayCopy方
- java web会话监听并使用spring注入
bewithme
Java Web
在java web应用中,当你想在建立会话或移除会话时,让系统做某些事情,比如说,统计在线用户,每当有用户登录时,或退出时,那么可以用下面这个监听器来监听。
import java.util.ArrayList;
import java.ut
- NoSQL数据库之Redis数据库管理(Redis的常用命令及高级应用)
bijian1013
redis数据库NoSQL
一 .Redis常用命令
Redis提供了丰富的命令对数据库和各种数据库类型进行操作,这些命令可以在Linux终端使用。
a.键值相关命令
b.服务器相关命令
1.键值相关命令
&
- java枚举序列化问题
bingyingao
java枚举序列化
对象在网络中传输离不开序列化和反序列化。而如果序列化的对象中有枚举值就要特别注意一些发布兼容问题:
1.加一个枚举值
新机器代码读分布式缓存中老对象,没有问题,不会抛异常。
老机器代码读分布式缓存中新对像,反序列化会中断,所以在所有机器发布完成之前要避免出现新对象,或者提前让老机器拥有新增枚举的jar。
2.删一个枚举值
新机器代码读分布式缓存中老对象,反序列
- 【Spark七十八】Spark Kyro序列化
bit1129
spark
当使用SparkContext的saveAsObjectFile方法将对象序列化到文件,以及通过objectFile方法将对象从文件反序列出来的时候,Spark默认使用Java的序列化以及反序列化机制,通常情况下,这种序列化机制是很低效的,Spark支持使用Kyro作为对象的序列化和反序列化机制,序列化的速度比java更快,但是使用Kyro时要注意,Kyro目前还是有些bug。
Spark
- Hybridizing OO and Functional Design
bookjovi
erlanghaskell
推荐博文:
Tell Above, and Ask Below - Hybridizing OO and Functional Design
文章中把OO和FP讲的深入透彻,里面把smalltalk和haskell作为典型的两种编程范式代表语言,此点本人极为同意,smalltalk可以说是最能体现OO设计的面向对象语言,smalltalk的作者Alan kay也是OO的最早先驱,
- Java-Collections Framework学习与总结-HashMap
BrokenDreams
Collections
开发中常常会用到这样一种数据结构,根据一个关键字,找到所需的信息。这个过程有点像查字典,拿到一个key,去字典表中查找对应的value。Java1.0版本提供了这样的类java.util.Dictionary(抽象类),基本上支持字典表的操作。后来引入了Map接口,更好的描述的这种数据结构。
&nb
- 读《研磨设计模式》-代码笔记-职责链模式-Chain Of Responsibility
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/**
* 业务逻辑:项目经理只能处理500以下的费用申请,部门经理是1000,总经理不设限。简单起见,只同意“Tom”的申请
* bylijinnan
*/
abstract class Handler {
/*
- Android中启动外部程序
cherishLC
android
1、启动外部程序
引用自:
http://blog.csdn.net/linxcool/article/details/7692374
//方法一
Intent intent=new Intent();
//包名 包名+类名(全路径)
intent.setClassName("com.linxcool", "com.linxcool.PlaneActi
- summary_keep_rate
coollyj
SUM
BEGIN
/*DECLARE minDate varchar(20) ;
DECLARE maxDate varchar(20) ;*/
DECLARE stkDate varchar(20) ;
DECLARE done int default -1;
/* 游标中 注册服务器地址 */
DE
- hadoop hdfs 添加数据目录出错
daizj
hadoophdfs扩容
由于原来配置的hadoop data目录快要用满了,故准备修改配置文件增加数据目录,以便扩容,但由于疏忽,把core-site.xml, hdfs-site.xml配置文件dfs.datanode.data.dir 配置项增加了配置目录,但未创建实际目录,重启datanode服务时,报如下错误:
2014-11-18 08:51:39,128 WARN org.apache.hadoop.h
- grep 目录级联查找
dongwei_6688
grep
在Mac或者Linux下使用grep进行文件内容查找时,如果给定的目标搜索路径是当前目录,那么它默认只搜索当前目录下的文件,而不会搜索其下面子目录中的文件内容,如果想级联搜索下级目录,需要使用一个“-r”参数:
grep -n -r "GET" .
上面的命令将会找出当前目录“.”及当前目录中所有下级目录
- yii 修改模块使用的布局文件
dcj3sjt126com
yiilayouts
方法一:yii模块默认使用系统当前的主题布局文件,如果在主配置文件中配置了主题比如: 'theme'=>'mythm', 那么yii的模块就使用 protected/themes/mythm/views/layouts 下的布局文件; 如果未配置主题,那么 yii的模块就使用 protected/views/layouts 下的布局文件, 总之默认不是使用自身目录 pr
- 设计模式之单例模式
come_for_dream
设计模式单例模式懒汉式饿汉式双重检验锁失败无序写入
今天该来的面试还没来,这个店估计不会来电话了,安静下来写写博客也不错,没事翻了翻小易哥的博客甚至与大牛们之间的差距,基础知识不扎实建起来的楼再高也只能是危楼罢了,陈下心回归基础把以前学过的东西总结一下。
*********************************
- 8、数组
豆豆咖啡
二维数组数组一维数组
一、概念
数组是同一种类型数据的集合。其实数组就是一个容器。
二、好处
可以自动给数组中的元素从0开始编号,方便操作这些元素
三、格式
//一维数组
1,元素类型[] 变量名 = new 元素类型[元素的个数]
int[] arr =
- Decode Ways
hcx2013
decode
A message containing letters from A-Z is being encoded to numbers using the following mapping:
'A' -> 1
'B' -> 2
...
'Z' -> 26
Given an encoded message containing digits, det
- Spring4.1新特性——异步调度和事件机制的异常处理
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- squid3(高命中率)缓存服务器配置
liyonghui160com
系统:centos 5.x
需要的软件:squid-3.0.STABLE25.tar.gz
1.下载squid
wget http://www.squid-cache.org/Versions/v3/3.0/squid-3.0.STABLE25.tar.gz
tar zxf squid-3.0.STABLE25.tar.gz &&
- 避免Java应用中NullPointerException的技巧和最佳实践
pda158
java
1) 从已知的String对象中调用equals()和equalsIgnoreCase()方法,而非未知对象。 总是从已知的非空String对象中调用equals()方法。因为equals()方法是对称的,调用a.equals(b)和调用b.equals(a)是完全相同的,这也是为什么程序员对于对象a和b这么不上心。如果调用者是空指针,这种调用可能导致一个空指针异常
Object unk
- 如何在Swift语言中创建http请求
shoothao
httpswift
概述:本文通过实例从同步和异步两种方式上回答了”如何在Swift语言中创建http请求“的问题。
如果你对Objective-C比较了解的话,对于如何创建http请求你一定驾轻就熟了,而新语言Swift与其相比只有语法上的区别。但是,对才接触到这个崭新平台的初学者来说,他们仍然想知道“如何在Swift语言中创建http请求?”。
在这里,我将作出一些建议来回答上述问题。常见的
- Spring事务的传播方式
uule
spring事务
传播方式:
新建事务
required
required_new - 挂起当前
非事务方式运行
supports
&nbs