In directed graphs, edges are one-way: the pair of vertices that defines each edge is an ordered pair that specifies a one-way adjacency. Many applications (for example, graphs that represent the web, scheduling constraints, or telephone calls) are naturally expressed in terms of directed graphs. The one-way restriction is natural, easy to enforce in our implementations, and seems innocuous; but it implies added combinatorial structure that has profound implications for our algorithms and makes working with directed graphs quite different from working with undirected graphs.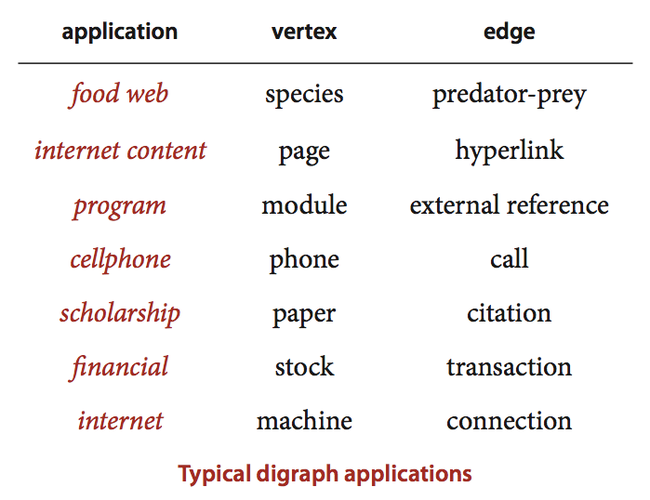
Glossary
Our definitions for directed graphs are nearly identical to those for undirected graphs but they are worth restating. The slight differences in the wording to account for edge directions imply structural properties that will be the focus of this section.
- A directed graph (or digraph) is a set of vertices and a collection of directed edges. Each directed edge connects an ordered pair of vertices.
- A directed path in a digraph is a sequence of vertices in which there is a (directed) edge pointing from each vertex in the sequence to its successor in the sequence. A directed cycle is a directed path with at least one edge whose first and last vertices are the same. A simple cycle is a cycle with no repeated edges or vertices (except the requisite repetition of the first and last vertices). The length of a path or a cycle is its number of edges.
public class Digraph {
private final int V;
private int E;
private Bag<Integer>[] adj;
/**
* Create an empty digraph with V vertices.
*
* @throws java.lang.IllegalArgumentException if V < 0
*/
public Digraph(int V) {
if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");
this.V = V;
this.E = 0;
adj = (Bag<Integer>[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag<Integer>();
}
}
/**
* Create a digraph from input stream.
*/
public Digraph(In in) {
try {
this.V = in.readInt();
if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");
adj = (Bag<Integer>[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag<Integer>();
}
int E = in.readInt();
if (E < 0) throw new IllegalArgumentException("Number of edges in a Digraph must be nonnegative");
for (int i = 0; i < E; i++) {
int v = in.readInt();
int w = in.readInt();
addEdge(v, w);
}
} catch (NoSuchElementException e) {
throw new InputMismatchException("Invalid input format in Digraph constructor");
}
}
/**
* Copy constructor.
*/
public Digraph(Digraph G) {
this(G.V());
this.E = G.E();
for (int v = 0; v < G.V(); v++) {
// reverse so that adjacency list is in same order as original
Stack<Integer> reverse = new Stack<Integer>();
for (int w : G.adj[v]) {
reverse.push(w);
}
for (int w : reverse) {
adj[v].add(w);
}
}
}
/**
* Return the number of vertices in the digraph.
*/
public int V() {
return V;
}
/**
* Return the number of edges in the digraph.
*/
public int E() {
return E;
}
/**
* Add the directed edge v->w to the digraph.
*
* @throws java.lang.IndexOutOfBoundsException unless both 0 <= v < V and 0 <= w < V
*/
public void addEdge(int v, int w) {
if (v < 0 || v >= V) throw new IndexOutOfBoundsException("vertex " + v + " is not between 0 and " + (V - 1));
if (w < 0 || w >= V) throw new IndexOutOfBoundsException("vertex " + w + " is not between 0 and " + (V - 1));
adj[v].add(w);
E++;
}
/**
* Return the list of vertices pointed to from vertex v as an Iterable.
*
* @throws java.lang.IndexOutOfBoundsException unless 0 <= v < V
*/
public Iterable<Integer> adj(int v) {
if (v < 0 || v >= V) throw new IndexOutOfBoundsException();
return adj[v];
}
/**
* Return the reverse of the digraph.
*/
public Digraph reverse() {
Digraph R = new Digraph(V);
for (int v = 0; v < V; v++) {
for (int w : adj(v)) {
R.addEdge(w, v);
}
}
return R;
}
/**
* Return a string representation of the digraph.
*/
public String toString() {
StringBuilder s = new StringBuilder();
String NEWLINE = System.getProperty("line.separator");
s.append(V + " vertices, " + E + " edges " + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(String.format("%d: ", v));
for (int w : adj[v]) {
s.append(String.format("%d ", w));
}
s.append(NEWLINE);
}
return s.toString();
}
}
Representation. We use the adjacency-lists representation,where an edge v->w is represented as a list node containing w in the linked list corresponding to v. This representation is essentially the same as for undirected graphs but is even more straight forward because each edge occurs just once, as shown on the facing page.
Input format. The code for the constructor that takes a digraph from an input stream is identical to the corresponding constructor in Graph—the input format is the same, but all edges are interpreted to be directed edges.In the list-of-edgesformat,apairv w is interpreted as an edge v->w.
Reversing a digraph. Digraph also adds to the API a method reverse() which returns a copy of the digraph, with all edges reversed. This method is sometimes needed in digraph processing because it allows clients to find the edges that point to each vertex, while adj() gives just vertices connected by edges that point from each vertex.
Symbolic names. It is also a simple matter to allow clients to use symbolic names in digraph applications. To implement a class SymbolDigraph like SymbolGraph, replace Graph by Digraph everywhere.
Single-source reachability. Given a digraph and a source vertex s, support queries of the form Is there a directed path from s to a given target vertex v? DirectedDFS on the facing page is a slight embellishment of DepthFirstSearch which is the answer to this question.
By adding a second constructor that takes a list of vertices, this API supports for clients the following generalization of the problem:
Multiple-source reachability. Given a digraph and a set of source vertices, support queries of the form Is there a directed path from any vertex in the set to a given target vertex v?
public class DirectedDFS {
private boolean[] marked; // marked[v] = true if v is reachable
// from source (or sources)
// single-source reachability
public DirectedDFS(Digraph G, int s) {
marked = new boolean[G.V()];
dfs(G, s);
}
// multiple-source reachability
public DirectedDFS(Digraph G, Iterable<Integer> sources) {
marked = new boolean[G.V()];
for (int v : sources)
dfs(G, v);
}
private void dfs(Digraph G, int v) {
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) dfs(G, w);
}
}
// is there a directed path from the source (or sources) to v?
public boolean marked(int v) {
return marked[v];
}
}
DFS marks all the vertices in a digraph reachable from a given set of sources in time proportional to the sum of the outdegrees of the vertices marked.
Finding paths in digraphs.
Single-source directed paths. Given a digraph and a source vertex s, support queries of the form Is there a directed path from s to a given target vertex v? If so, find such a path.
public class DepthFirstDirectedPaths {
private boolean[] marked; // marked[v] = true if v is reachable from s
private int[] edgeTo; // edgeTo[v] = last edge on path from s to v
private final int s; // source vertex
// single source
public DepthFirstDirectedPaths(Digraph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
dfs(G, s);
}
private void dfs(Digraph G, int v) {
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) {
edgeTo[w] = v;
dfs(G, w);
}
}
}
// is there a directed path from s to v?
public boolean hasPathTo(int v) {
return marked[v];
}
// return path from s to v; null if no such path
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)) return null;
Stack<Integer> path = new Stack<Integer>();
for (int x = v; x != s; x = edgeTo[x])
path.push(x);
path.push(s);
return path;
}
}
Single-source shortest directed paths. Given a digraph and a source vertex s, support queries of the form Is there a directed path from s to a given target vertex v? If so, find a shortest such path (one with a minimal number of edges).
public class BreadthFirstDirectedPaths {
private static final int INFINITY = Integer.MAX_VALUE;
private boolean[] marked; // marked[v] = is there an s->v path?
private int[] edgeTo; // edgeTo[v] = last edge on shortest s->v path
private int[] distTo; // distTo[v] = length of shortest s->v path
// single source
public BreadthFirstDirectedPaths(Digraph G, int s) {
marked = new boolean[G.V()];
distTo = new int[G.V()];
edgeTo = new int[G.V()];
for (int v = 0; v < G.V(); v++) distTo[v] = INFINITY;
bfs(G, s);
}
// multiple sources
public BreadthFirstDirectedPaths(Digraph G, Iterable<Integer> sources) {
marked = new boolean[G.V()];
distTo = new int[G.V()];
edgeTo = new int[G.V()];
for (int v = 0; v < G.V(); v++) distTo[v] = INFINITY;
bfs(G, sources);
}
// BFS from single source
private void bfs(Digraph G, int s) {
Queue<Integer> q = new Queue<Integer>();
marked[s] = true;
distTo[s] = 0;
q.enqueue(s);
while (!q.isEmpty()) {
int v = q.dequeue();
for (int w : G.adj(v)) {
if (!marked[w]) {
edgeTo[w] = v;
distTo[w] = distTo[v] + 1;
marked[w] = true;
q.enqueue(w);
}
}
}
}
// BFS from multiple sources
private void bfs(Digraph G, Iterable<Integer> sources) {
Queue<Integer> q = new Queue<Integer>();
for (int s : sources) {
marked[s] = true;
distTo[s] = 0;
q.enqueue(s);
}
while (!q.isEmpty()) {
int v = q.dequeue();
for (int w : G.adj(v)) {
if (!marked[w]) {
edgeTo[w] = v;
distTo[w] = distTo[v] + 1;
marked[w] = true;
q.enqueue(w);
}
}
}
}
// length of shortest path from s (or sources) to v
public int distTo(int v) {
return distTo[v];
}
// is there a directed path from s (or sources) to v?
public boolean hasPathTo(int v) {
return marked[v];
}
// shortest path from s (or sources) to v; null if no such path
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)) return null;
Stack<Integer> path = new Stack<Integer>();
int x;
for (x = v; distTo[x] != 0; x = edgeTo[x])
path.push(x);
path.push(x);
return path;
}
}
Cycles and DAGs
Directed cycles are of particular importance in applications that involve processing digraphs. To motivate the study of the role of directed cycles in digraph processing we consider, as a running example, the following prototypical application where digraph models arise directly:
Scheduling problems. A widely applicable problem-solving model has to do with arranging for the completion of a set of jobs, under a set of constraints, by specifying when and how the jobs are to be performed. Constraints might involve functions of the time taken or other resources consumed by the jobs. The most important type of constraints is precedence constraints, which specify that certain tasks must be performed before certain others. Different types of additional constraints lead to many different types of scheduling problems, of varying difficulty.
Precedence-constrained scheduling. Given a set of jobs to be completed, with precedence constraints that specify that certain jobs have to be completed before certain other jobs are begun, how can we schedule the jobs such that they are all completed while still respecting the constraints?
For any such problem, a digraph model is immediate, with vertices corresponding to jobs and directed edges corresponding to precedence constraints. In digraphs, precedence-constrained scheduling amounts to the following fundamental problem:
Topological sort. Given a digraph, put the vertices in order such that all its directed edges point from a ver- tex earlier in the order to a vertex later in the order (or report that doing so is not possible).
Cycles in digraphs. If job x must be completed before job y, job y before job z, and job z before job x, then someone has made a mistake, because those three constraints cannot all be satisfied. In general, if a precedence-constrained scheduling problem has a directed cycle, then there is no feasible solution. To check for such errors, we need to be able to solve the following problem: Directed cycle detection. Does a given digraph have a directed cycle? If so, find the vertices on some such cycle, in order from some vertex back to itself. A directed acyclic graph (DAG) is a digraph with no directed cycles.
public class DirectedCycle {
private boolean[] marked; // marked[v] = has vertex v been marked?
private int[] edgeTo; // edgeTo[v] = previous vertex on path to v
private boolean[] onStack; // onStack[v] = is vertex on the stack?
private Stack<Integer> cycle; // directed cycle (or null if no such cycle)
public DirectedCycle(Digraph G) {
marked = new boolean[G.V()];
onStack = new boolean[G.V()];
edgeTo = new int[G.V()];
for (int v = 0; v < G.V(); v++)
if (!marked[v]) dfs(G, v);
}
// check that algorithm computes either the topological order or finds a directed cycle
private void dfs(Digraph G, int v) {
onStack[v] = true;
marked[v] = true;
for (int w : G.adj(v)) {
// short circuit if directed cycle found
if (cycle != null) return;
//found new vertex, so recur
else if (!marked[w]) {
edgeTo[w] = v;
dfs(G, w);
}
// trace back directed cycle
else if (onStack[w]) {
cycle = new Stack<Integer>();
for (int x = v; x != w; x = edgeTo[x]) {
cycle.push(x);
}
cycle.push(w);
cycle.push(v);
}
}
onStack[v] = false;
}
public boolean hasCycle() {
return cycle != null;
}
public Iterable<Integer> cycle() {
return cycle;
}
// certify that digraph is either acyclic or has a directed cycle
private boolean check(Digraph G) {
if (hasCycle()) {
// verify cycle
int first = -1, last = -1;
for (int v : cycle()) {
if (first == -1) first = v;
last = v;
}
if (first != last) {
System.err.printf("cycle begins with %d and ends with %d\n", first, last);
return false;
}
}
return true;
}
}
Depth-first orders and topological sort. Precedence-constrained scheduling amounts to computing a topological order for the vertices of a DAG, a digraph has a topological order if and only if it is a DAG.
Remarkably, it turns out that we have already seen an algorithm for topological sort: a one-line addition to our standard recursive DFS does the job! To convince you of this fact, we begin with the class DepthFirstOrder on page 580. It is based on the idea that depth-first search visits each vertex exactly once. If we save the vertex given as argument to the recursive dfs() in a data structure, then iterate through that data structure, we see all the graph vertices, in order determined by the nature of the data structure and by whether we do the save before or after the recursive calls. Three vertex orderings are of interest in typical applications:
■ Preorder : Put the vertex on a queue before the recursive calls.
■ Postorder : Put the vertex on a queue after the recursive calls.
■ Reverse postorder : Put the vertex on a stack after the recursive calls.
A trace of DepthFirstOrder for our sample DAG is given on the facing page. It is simple to implement and supports pre(), post(), and reversePost() methods that are useful for advanced graph-processing algorithms. For example, order() in Topological consists of a call on reversePost().
public class DepthFirstOrder {
private boolean[] marked; // marked[v] = has v been marked in dfs?
private int[] pre; // pre[v] = preorder number of v
private int[] post; // post[v] = postorder number of v
private Queue<Integer> preorder; // vertices in preorder
private Queue<Integer> postorder; // vertices in postorder
private int preCounter; // counter or preorder numbering
private int postCounter; // counter for postorder numbering
// depth-first search preorder and postorder in a digraph
public DepthFirstOrder(Digraph G) {
pre = new int[G.V()];
post = new int[G.V()];
postorder = new Queue<Integer>();
preorder = new Queue<Integer>();
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++)
if (!marked[v]) dfs(G, v);
}
// depth-first search preorder and postorder in an edge-weighted digraph
public DepthFirstOrder(EdgeWeightedDigraph G) {
pre = new int[G.V()];
post = new int[G.V()];
postorder = new Queue<Integer>();
preorder = new Queue<Integer>();
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++)
if (!marked[v]) dfs(G, v);
}
// run DFS in digraph G from vertex v and compute preorder/postorder
private void dfs(Digraph G, int v) {
marked[v] = true;
pre[v] = preCounter++;
preorder.enqueue(v);
for (int w : G.adj(v)) {
if (!marked[w]) {
dfs(G, w);
}
}
postorder.enqueue(v);
post[v] = postCounter++;
}
// run DFS in edge-weighted digraph G from vertex v and compute preorder/postorder
private void dfs(EdgeWeightedDigraph G, int v) {
marked[v] = true;
pre[v] = preCounter++;
preorder.enqueue(v);
for (DirectedEdge e : G.adj(v)) {
int w = e.to();
if (!marked[w]) {
dfs(G, w);
}
}
postorder.enqueue(v);
post[v] = postCounter++;
}
public int pre(int v) {
return pre[v];
}
public int post(int v) {
return post[v];
}
// return vertices in postorder as an Iterable
public Iterable<Integer> post() {
return postorder;
}
// return vertices in preorder as an Iterable
public Iterable<Integer> pre() {
return preorder;
}
// return vertices in reverse postorder as an Iterable
public Iterable<Integer> reversePost() {
Stack<Integer> reverse = new Stack<Integer>();
for (int v : postorder)
reverse.push(v);
return reverse;
}
// check that pre() and post() are consistent with pre(v) and post(v)
private boolean check(Digraph G) {
// check that post(v) is consistent with post()
int r = 0;
for (int v : post()) {
if (post(v) != r) {
StdOut.println("post(v) and post() inconsistent");
return false;
}
r++;
}
// check that pre(v) is consistent with pre()
r = 0;
for (int v : pre()) {
if (pre(v) != r) {
StdOut.println("pre(v) and pre() inconsistent");
return false;
}
r++;
}
return true;
}
}
Reverse post order in a DAG is a topological sort. With DFS,we can topologically sort a DAG in time proportional to V+E.
public class Topological {
private Iterable<Integer> order; // topological order
// topological sort in a digraph
public Topological(Digraph G) {
DirectedCycle finder = new DirectedCycle(G);
if (!finder.hasCycle()) {
DepthFirstOrder dfs = new DepthFirstOrder(G);
order = dfs.reversePost();
}
}
// topological sort in an edge-weighted digraph
public Topological(EdgeWeightedDigraph G) {
EdgeWeightedDirectedCycle finder = new EdgeWeightedDirectedCycle(G);
if (!finder.hasCycle()) {
DepthFirstOrder dfs = new DepthFirstOrder(G);
order = dfs.reversePost();
}
}
// return topological order if a DAG; null otherwise
public Iterable<Integer> order() {
return order;
}
// does digraph have a topological order?
public boolean hasOrder() {
return order != null;
}
public static void main(String[] args) {
String filename = args[0];
String delimiter = args[1];
SymbolDigraph sg = new SymbolDigraph(filename, delimiter);
Topological topological = new Topological(sg.G());
for (int v : topological.order()) {
System.out.println(sg.name(v));
}
}
}