动态规划算法学习十例之三
例一:
给出N台电脑和K辆卡车,要求每辆卡车至少放一台电脑。问共有多少种放法运走这些电脑?
数据范围N (1<=N<=200) and K(1<=K<=N)。
[输入输出]:
输入的每一行是空格隔开的电脑数n和卡车数k ,输出对应的运法总数。
[样例]:
Sample Input
1 1
7 3
0 0
Sample Output
1
4
[解题分析]:
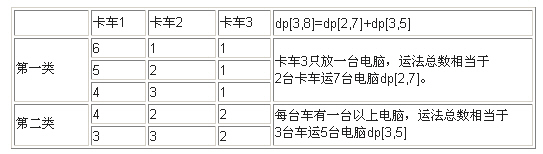
分析:典型dp,状态转移方程dp[i][j]=dp[i-1][j-1]+dp[i][j-i];
dp[i][j]表示i辆卡车装j台电脑的方法数。
例如:8台电脑3台车
例二 最小邮票数
题目描述:
有若干张邮票,要求从中选取最少的邮票张数凑成一个给定的总值。
如,有1分,3分,3分,3分,4分五张邮票,要求凑成10分,则使用3张邮票:3分、3分、4分即可。
输入:
有多组数据,对于每组数据,首先是要求凑成的邮票总值M,M<100。然后是一个数N,N〈20,表示有N张邮票。接下来是N个正整数,分别表示这N张邮票的面值,且以升序排列。
输出:
对于每组数据,能够凑成总值M的最少邮票张数。若无解,输出0。
样例输入:
10
5
1 3 3 3 4
样例输出:
3
给出N台电脑和K辆卡车,要求每辆卡车至少放一台电脑。问共有多少种放法运走这些电脑?
数据范围N (1<=N<=200) and K(1<=K<=N)。
[输入输出]:
输入的每一行是空格隔开的电脑数n和卡车数k ,输出对应的运法总数。
[样例]:
Sample Input
1 1
7 3
0 0
Sample Output
1
4
[解题分析]:
分析:典型dp,状态转移方程dp[i][j]=dp[i-1][j-1]+dp[i][j-i];
dp[i][j]表示i辆卡车装j台电脑的方法数。
例如:8台电脑3台车

import java.util.*;
public class Main{
private long dp[][]=new long[201][201];
public Main(){
init();
}
private void init(){
for(int i=1;i<201;i++)
{
dp[i][i]=dp[1][i]=dp[i][0]=dp[0][i]=1;
}
for(int i=2;i<201;i++)
{
for(int j=i+1;j<201;j++)
{
dp[i][j]=dp[i-1][j-1]+dp[i][j-i];
}
}
}
public long dp(int k,int n){
return dp[k][n];
}
public static void main(String args[]){
Scanner in=new Scanner(System.in);
Main m=new Main();
while(true){
int n=in.nextInt();
int k=in.nextInt();
if(n==0 && k==0) break;
System.out.println(m.dp(k,n));
}
}
}
例二 最小邮票数
题目描述:
有若干张邮票,要求从中选取最少的邮票张数凑成一个给定的总值。
如,有1分,3分,3分,3分,4分五张邮票,要求凑成10分,则使用3张邮票:3分、3分、4分即可。
输入:
有多组数据,对于每组数据,首先是要求凑成的邮票总值M,M<100。然后是一个数N,N〈20,表示有N张邮票。接下来是N个正整数,分别表示这N张邮票的面值,且以升序排列。
输出:
对于每组数据,能够凑成总值M的最少邮票张数。若无解,输出0。
样例输入:
10
5
1 3 3 3 4
样例输出:
3
import java.util.Scanner;
public class Main{
static int INF=Integer.MAX_VALUE;
public static void main(String args[]) {
Scanner in=new Scanner(System.in);
while(true) {
int m=in.nextInt();
int n=in.nextInt();
int[] w=new int[n];
int[] dp=new int[m+1];
for(int i=0;i<n;++i) w[i]=in.nextInt();
for(int i=1;i <= m; ++i) dp[i] = INF;//dp[i]表示凑成总值为i时所需的的最小邮票张数
dp[0]=0;
for(int i=0;i<n;++i) {
// System.out.println("i==================="+i);
for(int j = m;j>=w[i];--j) {
if(dp[j-w[i]] == INF) continue;
else{
dp[j]=Math.min(dp[j],dp[j-w[i]]+1);
// System.out.println("dp["+j+"]="+dp[j]);
}
}
}
if(dp[m] == INF) System.out.println("0");
else
System.out.printf("%d\n", dp[m]);
}
}
}