动态规划算法学习十例之十
凸多边形最优三角剖分
一凸8边形P的顶点顺时针为{v1,v2,… ,v8},任意两顶点间的线段的权重由矩阵D给出。
若vi与vj是P上不相邻的两个顶点,则线段vivj 称为P的一条弦。求P的一个弦的集合T,使得T中所有的弦恰好将P 分割成互不重迭的三角形,且各三角形的权重之和为最小(一个三角形的权重是其各边的权重之和)。
/*
int graph[][]={
{0, 14, 25, 27, 10, 11, 24, 16},
{14, 0, 18, 15, 27, 28, 16, 14},
{25, 18, 0, 19, 14, 19, 16, 10},
{27, 15, 19, 0, 22, 23, 15, 14},
{10, 27, 14, 22, 0, 14, 13, 20},
{11, 28, 19, 23, 14, 0, 15, 18},
{24, 16, 16, 15, 13, 15, 0, 27},
{16, 14, 10, 14, 20, 18, 27, 0}
};*/
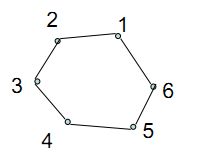
解答:题目中顶点坐标编号从1开始,为了方便编程,将顶点从0开始,顶点的编号变为0到7。定义t[i][j],0=<i<j<n为凸多边形{Vi,Vi,…Vj}的最优三角剖分所对应的权函数值,退化的两点多边形{Vi,Vi+1}的权值为0。要计算凸n边形的最优权值为t[0][n-1]。
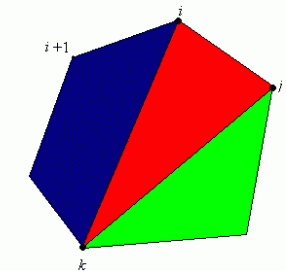
由于退化的两点多边形{Vi,Vi+1}的权值为0,t[i][i]=0。最优子结构的性质,t[i][j]的值是t[i][k]的值加上t[k][j]的值,再加上三角形ViVkVj的权值,其中,i<k<=j-1。K的位置有j-i-1个。因此可以在这j-i-1个未知中选出使t[i][j]值达到最小的位置,递归式为: t[i][j]=0 (j-i<=1)
t[i][j]=t[i][k]+t[k][j]+w(i,k,j) (j-i>=2)
运行:
C:\java>java TestTriangulation
最优剖分总权值
24
剖分时添加的线段
V0-V4
V1-V4
V2-V4
一凸8边形P的顶点顺时针为{v1,v2,… ,v8},任意两顶点间的线段的权重由矩阵D给出。
若vi与vj是P上不相邻的两个顶点,则线段vivj 称为P的一条弦。求P的一个弦的集合T,使得T中所有的弦恰好将P 分割成互不重迭的三角形,且各三角形的权重之和为最小(一个三角形的权重是其各边的权重之和)。
/*
int graph[][]={
{0, 14, 25, 27, 10, 11, 24, 16},
{14, 0, 18, 15, 27, 28, 16, 14},
{25, 18, 0, 19, 14, 19, 16, 10},
{27, 15, 19, 0, 22, 23, 15, 14},
{10, 27, 14, 22, 0, 14, 13, 20},
{11, 28, 19, 23, 14, 0, 15, 18},
{24, 16, 16, 15, 13, 15, 0, 27},
{16, 14, 10, 14, 20, 18, 27, 0}
};*/
解答:题目中顶点坐标编号从1开始,为了方便编程,将顶点从0开始,顶点的编号变为0到7。定义t[i][j],0=<i<j<n为凸多边形{Vi,Vi,…Vj}的最优三角剖分所对应的权函数值,退化的两点多边形{Vi,Vi+1}的权值为0。要计算凸n边形的最优权值为t[0][n-1]。
由于退化的两点多边形{Vi,Vi+1}的权值为0,t[i][i]=0。最优子结构的性质,t[i][j]的值是t[i][k]的值加上t[k][j]的值,再加上三角形ViVkVj的权值,其中,i<k<=j-1。K的位置有j-i-1个。因此可以在这j-i-1个未知中选出使t[i][j]值达到最小的位置,递归式为: t[i][j]=0 (j-i<=1)
t[i][j]=t[i][k]+t[k][j]+w(i,k,j) (j-i>=2)

public class TestTriangulation{
int t[][];
int s[][];
int graph[][];
int n;
public TestTriangulation(int n,int[][] graph){
this.n=n;
this.graph=graph;
t=new int[n][n];
s=new int[n][n];
}
private int w(int m, int n, int p){
return graph[m][n] + graph[m][p] + graph[n][p];
}
private void sp(int m, int n)//输出最优剖分需要添加的线段
{
if (n-m<=2)
return;
if(s[m][n]-m>=2){
System.out.printf("V%d-V%d\n", m, s[m][n]);
sp(m, s[m][n]);
}
if (n-s[m][n]>=2){
System.out.printf("V%d-V%d\n", s[m][n], n);
sp(s[m][n], n);
}
}
public int minWeight(){
int j, u;
for (int r=2; r<=n-1; r++)
for (int i=0; i<n-r; i++){
j = i + r;
t[i][j] =t[i][i+1] + t[i+1][j] +w(i, i+1, j);
s[i][j] = i+1;
for (int k=i+2; k<i+r; k++){
u = t[i][k] + t[k][j] + w(i, k, j);
if (u<t[i][j]){
t[i][j] = u;
s[i][j] = k;
}
}
}
return t[0][n-1];
}
public static void main(String args[]){
/*
int graph[][]={
{0, 14, 25, 27, 10, 11, 24, 16},
{14, 0, 18, 15, 27, 28, 16, 14},
{25, 18, 0, 19, 14, 19, 16, 10},
{27, 15, 19, 0, 22, 23, 15, 14},
{10, 27, 14, 22, 0, 14, 13, 20},
{11, 28, 19, 23, 14, 0, 15, 18},
{24, 16, 16, 15, 13, 15, 0, 27},
{16, 14, 10, 14, 20, 18, 27, 0}
};*/
int[][] graph = { { 0, 2, 2, 3, 1, 4 }, { 2, 0, 1, 5, 2, 3 }, { 2, 1, 0, 2, 1, 4 },
{ 3, 5, 2, 0, 6, 2 }, { 1, 2, 1, 6, 0, 1 }, { 4, 3, 4, 2, 1, 0 } };
TestTriangulation tri=new TestTriangulation(6,graph);
System.out.printf("最优剖分总权值\n");
System.out.printf("%d\n",tri.minWeight());
System.out.printf("剖分时添加的线段\n");
tri.sp(0,5);
}
}

运行:
C:\java>java TestTriangulation
最优剖分总权值
24
剖分时添加的线段
V0-V4
V1-V4
V2-V4