Some important applications of priority queues include simulation systems, where the keys correspond to event times, to be processed in chronological order; job scheduling, where the keys correspond to priorities indicating which tasks are to be performed first; and numerical computations, where the keys represent computational errors, indicating in which order we should deal with them.
We can use any priority queue as the basis for a sorting algorithm by inserting a sequence of items, then successively removing the smallest to get them out, in order. An important sorting algorithm known as heapsort also follows naturally from our heap-based priority-queue implementations.
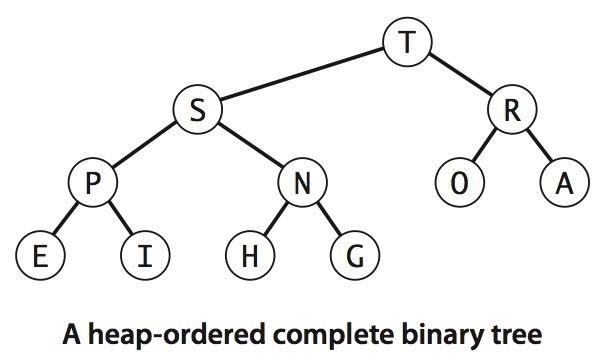
Heap definitions The binary heap is a data structure that can efficiently support the basic priority-queue operations. In a binary heap, the keys are stored in an array such that each key is guaranteed to be larger than (or equal to) the keys at two other specific positions. In turn, each of those keys must be larger than (or equal to) two additional keys, and so forth. This ordering is easy to see if we view the keys as being in a binary tree structure with edges from each key to the two keys known to be smaller. Here is the definition: A binary tree is heap-ordered if the key in each node is larger than or equal to the keys in that node’s two children (if any).
Binary heap representation. If we use a linked representation for heap-ordered binary trees, we would need to have three links associated with each key to allow travel up and down the tree (each node would have one pointer to its parent and one to each child). It is particularly convenient, instead, to use a complete binary tree like the one drawn at below. We draw such a structure by placing the root node and then proceeding down the page and from left to right, drawing and connecting two nodes beneath each node on the previous level until we have drawn N nodes. Complete trees provide the opportunity to use a compact array representation that does not involve explicit links. Specifically, we represent complete binary trees sequentially within an array by putting the nodes in level order, with the root at position 1, its children at positions 2 and 3, their children in positions 4, 5, 6, and 7, and so on.
Algorithms on heaps We represent a heap of size N in private array pq[] of length N + 1, with pq[0] unused and the heap in pq[1] through pq[N]. As for sorting algorithms, we access keys only through private helper functions less() and exch(), but since all items are in the instance variable pq[], we use the more compact implementations next that do not involve passing the array name as a parameter. The heap operations that we consider work by first making a simple modification that could violate the heap condition, then traveling through the heap, modifying the heap as required to ensure that the heap condition is satisfied everywhere. We refer to this process as reheapifying, or restoring heap order.
There are two cases. When the priority of some node is increased (or a new node is added at the bottom of a heap), we have to travel up the heap to restore the heap order. When the priority of some node is decreased (for example, if we replace the node at the root with a new node that has a smaller key), we have to travel down the heap to restore the heap order. First, we will consider how to implement these two basic auxiliary operations; then, we shall see how to use them to implement insert and remove the maximum.
Bottom-up reheapify (swim). If the heap order is violated because a node’s key becomes larger than that node’s parent’s key, then we can make progress toward fixing the violation by exchanging the node with its parent. After the exchange, the node is larger than both its children (one is the old parent, and the other is smaller than the old parent because it was a child of that node) but the node may still be larger than its parent. We can fix that violation in the same way, and so forth, moving up the heap until we reach a node with a larger key, or the root. Coding this process is straightforward when you keep in mind that the parent of the node at position k in a heap is at position k/2. The loop in swim() preserves the invariant that the only place the heap order could be violated is when the node at position k might be larger than its parent. Therefore, when we get to a place where that node is not larger than its parent, we know that the heap order is satisfied throughout the heap. To justify the method’s name, we think of the new node, having too large a key, as having to swim to a higher level in the heap.
private void swim(int k) {
while (k > 1 && less(k/2, k)) {
exch(k/2, k);
k = k/2;
}
}
Top-down reheapify(sink). If the heap order is violated because a node’s key becomes smaller than one or both of that node’s children’s keys, then we can make progress toward fixing the violation by exchanging the node with the larger of its two children. This switch may cause a violation at the child; we fix that violation in the same way, and so forth, moving down the heap until we reach a node with both children smaller (or equal), or the bottom. The code again follows directly from the fact that the children of the node at position k in a heap are at positions 2k and 2k+1. To justify the method’s name, we think about the node, having too small a key, as having to sink to a lower level in the heap.
private void sink(int k) {
while (2*k <= N) {
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
These sink() and swim() operations provide the basis for efficient implementation of the priority-queue algorithm.
public class MaxPQ<Key> implements Iterable<Key> {
private Key[] pq; // store items at indices 1 to N
private int N; // number of items on priority queue
private Comparator<Key> comparator; // optional Comparator
/**
* Create an empty priority queue with the given initial capacity.
*/
public MaxPQ(int capacity) {
pq = (Key[]) new Object[capacity + 1];
N = 0;
}
/**
* Create an empty priority queue.
*/
public MaxPQ() {
this(1);
}
/**
* Create an empty priority queue with the given initial capacity,
* using the given comparator.
*/
public MaxPQ(int initCapacity, Comparator<Key> comparator) {
this.comparator = comparator;
pq = (Key[]) new Object[initCapacity + 1];
N = 0;
}
/**
* Create an empty priority queue using the given comparator.
*/
public MaxPQ(Comparator<Key> comparator) {
this(1, comparator);
}
/**
* Create a priority queue with the given items.
* Takes time proportional to the number of items using sink-based heap construction.
*/
public MaxPQ(Key[] keys) {
N = keys.length;
pq = (Key[]) new Object[keys.length + 1];
for (int i = 0; i < N; i++)
pq[i + 1] = keys[i];
for (int k = N / 2; k >= 1; k--)
sink(k);
assert isMaxHeap();
}
/**
* Is the priority queue empty?
*/
public boolean isEmpty() {
return N == 0;
}
/**
* Return the number of items on the priority queue.
*/
public int size() {
return N;
}
/**
* Return the largest key on the priority queue.
*
* @throws java.util.NoSuchElementException
* if priority queue is empty.
*/
public Key max() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
return pq[1];
}
// helper function to double the size of the heap array
private void resize(int capacity) {
assert capacity > N;
Key[] temp = (Key[]) new Object[capacity];
for (int i = 1; i <= N; i++) temp[i] = pq[i];
pq = temp;
}
/**
* Add a new key to the priority queue.
*/
public void insert(Key x) {
// double size of array if necessary
if (N >= pq.length - 1) resize(2 * pq.length);
// add x, and percolate it up to maintain heap invariant
pq[++N] = x;
swim(N);
assert isMaxHeap();
}
/**
* Delete and return the largest key on the priority queue.
*
* @throws java.util.NoSuchElementException
* if priority queue is empty.
*/
public Key delMax() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
Key max = pq[1];
exch(1, N--);
sink(1);
pq[N + 1] = null; // to avoid loiterig and help with garbage collection
if ((N > 0) && (N == (pq.length - 1) / 4)) resize(pq.length / 2);
assert isMaxHeap();
return max;
}
/**
* ********************************************************************
* Helper functions to restore the heap invariant.
* ********************************************************************
*/
private void swim(int k) {
while (k > 1 && less(k / 2, k)) {
exch(k, k / 2);
k = k / 2;
}
}
private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(j, j + 1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
/**
* ********************************************************************
* Helper functions for compares and swaps.
* ********************************************************************
*/
private boolean less(int i, int j) {
if (comparator == null) {
return ((Comparable<Key>) pq[i]).compareTo(pq[j]) < 0;
} else {
return comparator.compare(pq[i], pq[j]) < 0;
}
}
private void exch(int i, int j) {
Key swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
}
// is pq[1..N] a max heap?
private boolean isMaxHeap() {
return isMaxHeap(1);
}
// is subtree of pq[1..N] rooted at k a max heap?
private boolean isMaxHeap(int k) {
if (k > N) return true;
int left = 2 * k, right = 2 * k + 1;
if (left <= N && less(k, left)) return false;
if (right <= N && less(k, right)) return false;
return isMaxHeap(left) && isMaxHeap(right);
}
/***********************************************************************
* Iterator
**********************************************************************/
/**
* Return an iterator that iterates over all of the keys on the priority queue
* in descending order.
* <p/>
* The iterator doesn't implement <tt>remove()</tt> since it's optional.
*/
public Iterator<Key> iterator() {
return new HeapIterator();
}
private class HeapIterator implements Iterator<Key> {
// create a new pq
private MaxPQ<Key> copy;
// add all items to copy of heap
// takes linear time since already in heap order so no keys move
public HeapIterator() {
if (comparator == null) copy = new MaxPQ<Key>(size());
else copy = new MaxPQ<Key>(size(), comparator);
for (int i = 1; i <= N; i++)
copy.insert(pq[i]);
}
public boolean hasNext() {
return !copy.isEmpty();
}
public void remove() {
throw new UnsupportedOperationException();
}
public Key next() {
if (!hasNext()) throw new NoSuchElementException();
return copy.delMax();
}
}
}
In an N-key priority queue, the heap algorithms require no more than 1 + lg N compares for insert and no more than 2lg N compares for remove the maximum.
Index priority queue. In many applications, it makes sense to allow clients to refer to items that are already on the priority queue. One easy way to do so is to associate a unique integer index with each item. Moreover, it is often the case that clients have a universe of items of a known size N and perhaps are using (parallel) arrays to store information about the items, so other unrelated client code might already be using an integer index to refer to items.
public class IndexMinPQ<Key extends Comparable<Key>> implements Iterable<Integer> {
private int NMAX; // maximum number of elements on PQ
private int N; // number of elements on PQ
private int[] pq; // binary heap using 1-based indexing
private int[] qp; // inverse of pq - qp[pq[i]] = pq[qp[i]] = i
private Key[] keys; // keys[i] = priority of i
/**
* Create an empty indexed priority queue with indices between 0 and NMAX-1.
*
* @throws java.lang.IllegalArgumentException
* if NMAX < 0
*/
public IndexMinPQ(int NMAX) {
if (NMAX < 0) throw new IllegalArgumentException();
this.NMAX = NMAX;
keys = (Key[]) new Comparable[NMAX + 1]; // make this of length NMAX??
pq = new int[NMAX + 1];
qp = new int[NMAX + 1]; // make this of length NMAX??
for (int i = 0; i <= NMAX; i++) qp[i] = -1;
}
/**
* Is the priority queue empty?
*/
public boolean isEmpty() {
return N == 0;
}
/**
* Is i an index on the priority queue?
*
* @throws java.lang.IndexOutOfBoundsException
* unless (0 ≤ i < NMAX)
*/
public boolean contains(int i) {
if (i < 0 || i >= NMAX) throw new IndexOutOfBoundsException();
return qp[i] != -1;
}
/**
* Return the number of keys on the priority queue.
*/
public int size() {
return N;
}
/**
* Associate key with index i.
*
* @throws java.lang.IndexOutOfBoundsException
* unless 0 ≤ i < NMAX
* @throws java.lang.IllegalArgumentException
* if there already is an item associated with index i.
*/
public void insert(int i, Key key) {
if (i < 0 || i >= NMAX) throw new IndexOutOfBoundsException();
if (contains(i)) throw new IllegalArgumentException("index is already in the priority queue");
N++;
qp[i] = N;
pq[N] = i;
keys[i] = key;
swim(N);
}
/**
* Return the index associated with a minimal key.
*
* @throws java.util.NoSuchElementException
* if priority queue is empty.
*/
public int minIndex() {
if (N == 0) throw new NoSuchElementException("Priority queue underflow");
return pq[1];
}
/**
* Return a minimal key.
*
* @throws java.util.NoSuchElementException
* if priority queue is empty.
*/
public Key minKey() {
if (N == 0) throw new NoSuchElementException("Priority queue underflow");
return keys[pq[1]];
}
/**
* Delete a minimal key and return its associated index.
*
* @throws java.util.NoSuchElementException
* if priority queue is empty.
*/
public int delMin() {
if (N == 0) throw new NoSuchElementException("Priority queue underflow");
int min = pq[1];
exch(1, N--);
sink(1);
qp[min] = -1; // delete
keys[pq[N + 1]] = null; // to help with garbage collection
pq[N + 1] = -1; // not needed
return min;
}
/**
* Return the key associated with index i.
*
* @throws java.lang.IndexOutOfBoundsException
* unless 0 ≤ i < NMAX
* @throws java.util.NoSuchElementException
* no key is associated with index i
*/
public Key keyOf(int i) {
if (i < 0 || i >= NMAX) throw new IndexOutOfBoundsException();
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
else return keys[i];
}
/**
* Change the key associated with index i to the specified value.
*
* @throws java.lang.IndexOutOfBoundsException
* unless 0 ≤ i < NMAX
* @deprecated Replaced by changeKey()
*/
@Deprecated
public void change(int i, Key key) {
changeKey(i, key);
}
/**
* Change the key associated with index i to the specified value.
*
* @throws java.lang.IndexOutOfBoundsException
* unless 0 ≤ i < NMAX
* @throws java.util.NoSuchElementException
* no key is associated with index i
*/
public void changeKey(int i, Key key) {
if (i < 0 || i >= NMAX) throw new IndexOutOfBoundsException();
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
keys[i] = key;
swim(qp[i]);
sink(qp[i]);
}
/**
* Decrease the key associated with index i to the specified value.
*
* @throws java.lang.IndexOutOfBoundsException
* unless 0 ≤ i < NMAX
* @throws java.lang.IllegalArgumentException
* if key ≥ key associated with index i
* @throws java.util.NoSuchElementException
* no key is associated with index i
*/
public void decreaseKey(int i, Key key) {
if (i < 0 || i >= NMAX) throw new IndexOutOfBoundsException();
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
if (keys[i].compareTo(key) <= 0)
throw new IllegalArgumentException("Calling decreaseKey() with given argument would not strictly decrease the key");
keys[i] = key;
swim(qp[i]);
}
/**
* Increase the key associated with index i to the specified value.
*
* @throws java.lang.IndexOutOfBoundsException
* unless 0 ≤ i < NMAX
* @throws java.lang.IllegalArgumentException
* if key ≤ key associated with index i
* @throws java.util.NoSuchElementException
* no key is associated with index i
*/
public void increaseKey(int i, Key key) {
if (i < 0 || i >= NMAX) throw new IndexOutOfBoundsException();
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
if (keys[i].compareTo(key) >= 0)
throw new IllegalArgumentException("Calling increaseKey() with given argument would not strictly increase the key");
keys[i] = key;
sink(qp[i]);
}
/**
* Delete the key associated with index i.
*
* @throws java.lang.IndexOutOfBoundsException
* unless 0 ≤ i < NMAX
* @throws java.util.NoSuchElementException
* no key is associated with index i
*/
public void delete(int i) {
if (i < 0 || i >= NMAX) throw new IndexOutOfBoundsException();
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
int index = qp[i];
exch(index, N--);
swim(index);
sink(index);
keys[i] = null;
qp[i] = -1;
}
/**
* ***********************************************************
* General helper functions
* ************************************************************
*/
private boolean greater(int i, int j) {
return keys[pq[i]].compareTo(keys[pq[j]]) > 0;
}
private void exch(int i, int j) {
int swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
qp[pq[i]] = i;
qp[pq[j]] = j;
}
/**
* ***********************************************************
* Heap helper functions
* ************************************************************
*/
private void swim(int k) {
while (k > 1 && greater(k / 2, k)) {
exch(k, k / 2);
k = k / 2;
}
}
private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && greater(j, j + 1)) j++;
if (!greater(k, j)) break;
exch(k, j);
k = j;
}
}
/***********************************************************************
* Iterators
**********************************************************************/
/**
* Return an iterator that iterates over all of the elements on the
* priority queue in ascending order.
* <p/>
* The iterator doesn't implement <tt>remove()</tt> since it's optional.
*/
public Iterator<Integer> iterator() {
return new HeapIterator();
}
private class HeapIterator implements Iterator<Integer> {
// create a new pq
private IndexMinPQ<Key> copy;
// add all elements to copy of heap
// takes linear time since already in heap order so no keys move
public HeapIterator() {
copy = new IndexMinPQ<Key>(pq.length - 1);
for (int i = 1; i <= N; i++)
copy.insert(pq[i], keys[pq[i]]);
}
public boolean hasNext() {
return !copy.isEmpty();
}
public void remove() {
throw new UnsupportedOperationException();
}
public Integer next() {
if (!hasNext()) throw new NoSuchElementException();
return copy.delMin();
}
}
}
Index priority-queue client. The IndexMinPQ client Multiway solves the multiway merge problem: it merges together several sorted input streams into one sorted output stream. This problem arises in many applications: the streams might be the output of scientific instruments (sorted by time), lists of information from the web such as music or movies (sorted by title or artist name), commercial transactions (sorted by account number or time), or whatever. If you have the space, you might just read them all into an array and sort them, but with a priority queue, you can read input streams and put them in sorted order on the output no matter how long they are.
public class Multiway {
public static void merge(In[] streams) {
int N = streams.length;
IndexMinPQ<String> pq = new IndexMinPQ<String>(N);
for (int i = 0; i < N; i++)
if (!streams[i].isEmpty())
pq.insert(i, streams[i].readString());
// Extract and print min and read next from its stream.
while (!pq.isEmpty()) {
StdOut.print(pq.minKey() + " ");
int i = pq.delMin();
if (!streams[i].isEmpty())
pq.insert(i, streams[i].readString());
}
StdOut.println();
}
public static void main(String[] args) {
int N = args.length;
In[] streams = new In[N];
for (int i = 0; i < N; i++)
streams[i] = new In(args[i]);
merge(streams);
}
}
Heapsort
Heapsort breaks into two phases: heap construction, where we reorganize the original array into a heap, and the sortdown, where we pull the items out of the heap in decreasing order to build the sorted result. For consistency with the code we have studied, we use a maximum-oriented priority queue and repeatedly remove the maximum. Focusing on the task of sorting, we abandon the notion of hiding the representation of the priority queue and use swim() and sink() directly. Doing so allows us to sort an array without needing any extra space, by maintaining the heap within the array to be sorted.
Heap construction. How difficult is the process of building a heap from N given items? Certainly we can accomplish this task in time proportional to N log N, by proceeding from left to right through the array, using swim() to ensure that the items to the left of the scanning pointer make up a heap-ordered complete tree, like successive priority-queue insertions. A clever method that is much more efficient is to proceed from right to left, using sink() to make sub heaps as we go. Every position in the array is the root of a small subheap; sink() works for such sub heaps, as well. If the two children of a node are heaps, then calling sink() on that node makes the subtree rooted at the parent a heap. This process establishes the heap order inductively. The scan starts halfway back through the array because we can skip the subheaps of size 1. The scan ends at position 1, when we finish building the heap with one call to sink(). As the first phase of a sort, heap construction is a bit counterintuitive, because its goal is to produce a heap-ordered result, which has the largest item first in the array (and other larger items near the beginning), not at the end, where it is destined to finish. Sink-based heap construction uses fewer than 2N compares and fewer than N exchanges to construct a heap from N items.
Sortdown. Most of the work during heapsort is done during the second phase, where we remove the largest remaining item from the heap and put it into the array position vacated as the heap shrinks. This process is a bit like selection sort (taking the items in decreasing order instead of in increasing order), but it uses many fewer compares because the heap provides a much more efficient way to find the largest item in the unsorted part of the array.
public class Heap {
public static void sort(Comparable[] pq) {
int N = pq.length;
for (int k = N / 2; k >= 1; k--)
sink(pq, k, N);
while (N > 1) {
exch(pq, 1, N--);
sink(pq, 1, N);
}
}
/**
* ********************************************************************
* Helper functions to restore the heap invariant.
* ********************************************************************
*/
private static void sink(Comparable[] pq, int k, int N) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(pq, j, j + 1)) j++;
if (!less(pq, k, j)) break;
exch(pq, k, j);
k = j;
}
}
/**
* ********************************************************************
* Helper functions for comparisons and swaps.
* Indices are "off-by-one" to support 1-based indexing.
* ********************************************************************
*/
private static boolean less(Comparable[] pq, int i, int j) {
return pq[i - 1].compareTo(pq[j - 1]) < 0;
}
private static void exch(Object[] pq, int i, int j) {
Object swap = pq[i - 1];
pq[i - 1] = pq[j - 1];
pq[j - 1] = swap;
}
// is v < w ?
private static boolean less(Comparable v, Comparable w) {
return (v.compareTo(w) < 0);
}
/**
* ********************************************************************
* Check if array is sorted - useful for debugging
* *********************************************************************
*/
private static boolean isSorted(Comparable[] a) {
for (int i = 1; i < a.length; i++)
if (less(a[i], a[i - 1])) return false;
return true;
}
}
Above is a full implementation based on these ideas, the classical heapsort algorithm, which was invented by J. W. J. Williams and refined by R. W. Floyd in 1964. Although the loops in this program seem to do different tasks (the first constructs the heap, and the second destroys the heap for the sortdown), they are both built around the sink() method. We provide an implementation outside of our priority-queue API to highlight the simplicity of the sorting algorithm (eight lines of code for sort() and another eight lines of code for sink()) and to make it an in-place sort.
