UnionFind算法学习
算法来自Algorithms一书1.5节,在此备忘。
该书配套网站:http://algs4.cs.princeton.edu/15uf/
算法解决的问题
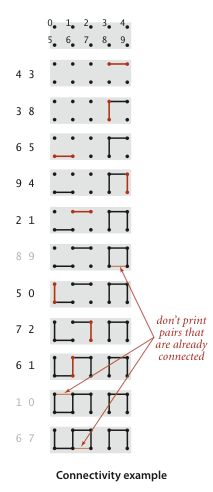
解决的是动态连通性问题,给定N个点和N个点之间的连通数据,例如:
N = 10(0,1,2,3,4,5,6,7,8,9)
连通数据:
(4,3)
(3,8)
(6,5)
(9,4)
(2,1)
(8,9)
(5,0)
(7,2)
(6,1)
(1,0)
(6,7)
效果图如下:
问题就是,如何判断给定的两个点是连通的?比如上图中,(8,9)、(1,0)、(6,7)都是连通的。如何判断这些节点中有多少个连通分量(孤岛,如上面的数据构成的节点就存在两个相互独立的孤岛)?
quick-find算法:
该算法的思路是创建一个长度为N的数组,数组的每一个元素表示一个点,依靠判断两个数组元素的值是否相同来判断这两个元素是否是连通的,数组元素的初始值为点的序号,表示他们互不相连。新加入一个连接时,需要将连接双方的每一个点的值都改成一致的。
public class QuickFindUF {
private int[] id;
private int count;
public QuickFindUF(int N){
id = new int[N];
for(int i = 0;i<N;i++){
id[i] = i;
}
count = N;
}
public int find(int p){
return id[p];
}
//union q to p
public void union(int p,int q){
int pId = find(p);
int qId = find(q);
if(pId==qId) return;
for(int i = 0;i<id.length;i++){
if(id[i]==qId){
id[i] = pId;
}
}
count--;
}
public boolean connected(int p,int q){
return find(p) == find(q);
}
public int count(){
return count;
}
public static void main(String[] args) {
int N = StdIn.readInt();
QuickFindUF uf = new QuickFindUF(N);
while(!StdIn.isEmpty()){
int p = StdIn.readInt();
int q = StdIn.readInt();
if(uf.connected(p, q)){
continue;
}
uf.union(p, q);
StdOut.println(p + " " + q);
}
StdOut.println(uf.count()+" compontents");
}
}
quick-union算法
quick-union算法在对节点值的定义上有所不同,表示的是父节点,从而把所有节点变成了树状结构。
quick-find算法的时间主要浪费在union上,改进的quick-union算法的union方法进行了优化,不需要遍历所有节点。这主要依赖于find方法,find方法查找的不是节点本身,而是节点所属的根节点:
public class QuickUnionUF {
private int[] id;
private int count;
public QuickUnionUF(int N){
id = new int[N];
for(int i = 0;i<N;i++){
id[i] = i;
}
count = N;
}
public int find(int p){
while(id[p]!=p){
p = id[p];
}
return id[p];
}
//union q to p
public void union(int p,int q){
int pId = find(p);
int qId = find(q);
if(pId==qId) return;
id[pId] = qId;
count--;
}
public boolean connected(int p,int q){
return find(p) == find(q);
}
public int count(){
return count;
}
public static void main(String[] args) {
int N = StdIn.readInt();
QuickUnionUF uf = new QuickUnionUF(N);
while(!StdIn.isEmpty()){
int p = StdIn.readInt();
int q = StdIn.readInt();
if(uf.connected(p, q)){
continue;
}
uf.union(p, q);
//StdOut.println(p + " " + q);
}
StdOut.println(uf.count()+" compontents");
}
}
加权重的quick-union算法
quick-union的缺点是,在最坏情况的输入数据时,最后形成的树可能是畸形的,树的深度很大,导致find方法查找根节点的时间代价越来越大。加权重的quick-union算法增加了每个节点的权重值。在初始时每个节点的权重是相同的,当节点不断地聚集,根节点的权重不断增大。union的时候,根据权重就能将小树连接到大树上,不会出现将大树连接到小树的情况,从而保证树的深度不会很大。
public class WeightedQuickUnionUF {
private int[] id;
private int[] weight;
private int count;
public WeightedQuickUnionUF(int N){
System.out.println("size=" +N);
id = new int[N];
weight = new int[N];
for(int i = 0;i<N;i++){
id[i] = i;
weight[i] = 1;
}
count = N;
}
public int find(int p){
while(id[p]!=p){
p = id[p];
}
return id[p];
}
//union q to p
public void union(int p,int q){
int pId = find(p);
int qId = find(q);
if(pId==qId) return;
if(weight[pId] < weight[qId]){
//connect p to q
id[pId] = qId;
weight[qId] += weight[pId];
}else{
//connect q to p
id[qId] = pId;
weight[pId] += weight[qId];
}
count--;
}
public boolean connected(int p,int q){
return find(p) == find(q);
}
public int count(){
return count;
}
public static void main(String[] args) {
int N = StdIn.readInt();
WeightedQuickUnionUF uf = new WeightedQuickUnionUF(N);
while(!StdIn.isEmpty()){
int p = StdIn.readInt();
int q = StdIn.readInt();
if(uf.connected(p, q)){
continue;
}
uf.union(p, q);
//StdOut.println(p + " " + q);
}
StdOut.println(uf.count()+" compontents");
}
}
总的来说,quick-find方法不是基于树来考虑的,跟多的是基于分组的思想,最终的结果是不同的孤岛中的点都保存着相同的组号。quick-union算法则是基于树的思想,两个树想连的时候,不会对树的子节点进行任何操作,仅仅是对树的根节点进行调整,这就避免了从新调整节点值的操作。这种情况下,如果再保证树的深度不是很大,就能迅速提高运行速度。