Trie树 单词查找树 键树（JAVA版附分析说明）
来源于英文“retrieval”. Trie树就是字符树，其核心思想就是空间换时间。
举个简单的例子。
给你100000个长度不超过10的单词。对于每一个单词，我们要判断他出没出现过，如果出现了，第一次出现第几个位置。
这题当然可以用hash来，但是我要介绍的是trie树。在某些方面它的用途更大。比如说对于某一个单词，我要询问它的前缀是否出现过。这样hash就不好搞了，而用trie还是很简单。
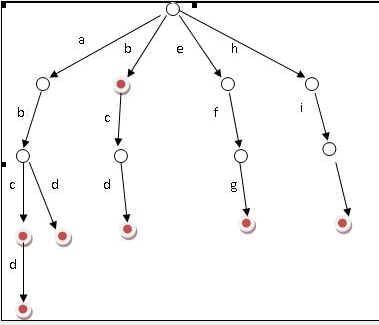
现在回到例子中，如果我们用最傻的方法，对于每一个单词，我们都要去查找它前面的单词中是否有它。那么这个算法的复杂度就是 O(n^2)。显然对于100000的范围难以接受。现在我们换个思路想。假设我要查询的单词是abcd，那么在他前面的单词中，以b，c，d，f之类开 头的我显然不必考虑。而只要找以a开头的中是否存在abcd就可以了。同样的，在以a开头中的单词中，我们只要考虑以b作为第二个字母的……这样一个树的 模型就渐渐清晰了……
假设有b，abc，abd，bcd，abcd，efg，hii这6个单词，我们构建的树就是这样的。
对于每一个节点，从根遍历到他的过程就是一个单词，如果这个节点被标记为红色，就表示这个单词存在，否则不存在。
那么，对于一个单词，我只要顺着他从根走到对应的节点，再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色，就相当于插入了这个单词。
我们可以看到，trie树每一层的节点数是26^i级别的。所以为了节省空间。我们用动态链表，或者用数组来模拟动态。空间的花费，不会超过单词数×单词长度。(转自一大牛)
Trie树的java代码 实现如下：
import java.util.ArrayList;
import java.util.List;
/**
* 单词查找树
*
* @author Jay Chang
* @since 2012-06-13
*/
class Trie {
/** 单词查找树根节点，根节点为一个空的节点 */
private Vertex root = new Vertex();
/** 单词查找树的节点(内部类) */
private class Vertex {
/** 单词出现次数统计 */
int wordCount;
/** 以某个前缀开头的单词，它的出现次数 */
int prefixCount;
/** 子节点用数组表示 */
Vertex[] vertexs = new Vertex[26];
/**
* 树节点的构造函数
*/
public Vertex() {
wordCount = 0;
prefixCount = 0;
}
}
/**
* 单词查找树构造函数
*/
public Trie() {
}
/**
* 向单词查找树添加一个新单词
*
* @param word
* 单词
*/
public void addWord(String word) {
addWord(root, word.toLowerCase());
}
/**
* 向单词查找树添加一个新单词
*
* @param root
* 单词查找树节点
* @param word
* 单词
*/
private void addWord(Vertex vertex, String word) {
if (word.length() == 0) {
vertex.wordCount++;
} else if (word.length() > 0) {
vertex.prefixCount++;
char c = word.charAt(0);
int index = c - 'a';
if (null == vertex.vertexs[index]) {
vertex.vertexs[index] = new Vertex();
}
addWord(vertex.vertexs[index], word.substring(1));
}
}
/**
* 统计某个单词出现次数
*
* @param word
* 单词
* @return 出现次数
*/
public int countWord(String word) {
return countWord(root, word);
}
/**
* 统计某个单词出现次数
*
* @param root
* 单词查找树节点
* @param word
* 单词
* @return 出现次数
*/
private int countWord(Vertex vertex, String word) {
if (word.length() == 0) {
return vertex.wordCount;
} else {
char c = word.charAt(0);
int index = c - 'a';
if (null == vertex.vertexs[index]) {
return 0;
} else {
return countWord(vertex.vertexs[index], word.substring(1));
}
}
}
/**
* 统计以某个前缀开始的单词，它的出现次数
*
* @param word
* 前缀
* @return 出现次数
*/
public int countPrefix(String word) {
return countPrefix(root, word);
}
/**
* 统计以某个前缀开始的单词，它的出现次数(前缀本身不算在内)
*
* @param root
* 单词查找树节点
* @param word
* 前缀
* @return 出现次数
*/
private int countPrefix(Vertex vertex, String prefixSegment) {
if (prefixSegment.length() == 0) {
return vertex.prefixCount;
} else {
char c = prefixSegment.charAt(0);
int index = c - 'a';
if (null == vertex.vertexs[index]) {
return 0;
} else {
return countPrefix(vertex.vertexs[index], prefixSegment.substring(1));
}
}
}
/**
* 调用深度递归算法得到所有单词
* @return 单词集合
*/
public List<String> listAllWords() {
List<String> allWords = new ArrayList<String>();
return depthSearchWords(allWords, root, "");
}
/**
* 递归生成所有单词
* @param allWords 单词集合
* @param vertex 单词查找树的节点
* @param wordSegment 单词片段
* @return 单词集合
*/
private List<String> depthSearchWords(List<String> allWords, Vertex vertex,
String wordSegment) {
Vertex[] vertexs = vertex.vertexs;
for (int i = 0; i < vertexs.length; i++) {
if (null != vertexs[i]) {
if (vertexs[i].wordCount > 0) {
allWords.add(wordSegment + (char)(i + 'a'));
if(vertexs[i].prefixCount > 0){
depthSearchWords(allWords, vertexs[i], wordSegment + (char)(i + 'a'));
}
} else {
depthSearchWords(allWords, vertexs[i], wordSegment + (char)(i + 'a'));
}
}
}
return allWords;
}
}
public class Main {
public static void main(String[] args) {
Trie trie = new Trie();
trie.addWord("abc");
trie.addWord("abcd");
trie.addWord("abcde");
trie.addWord("abcdef");
System.out.println(trie.countPrefix("abc"));
System.out.println(trie.countWord("abc"));
System.out.println(trie.listAllWords());
}
}