插入排序(insertion sorts)算法大串讲
插入排序(insertion sorts)算法大串讲
本文内容框架:
§1 基本插入排序算法和折半插入排序算法
§2 希尔排序(shell sort)算法
§3 图书馆排序(library sort)算法
§4 耐心排序(patience sort)算法
§5 小结
§1 基本插入排序算法和折半插入排序算法
插入排序(insertion sort)
插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置,直到全部插入完毕。
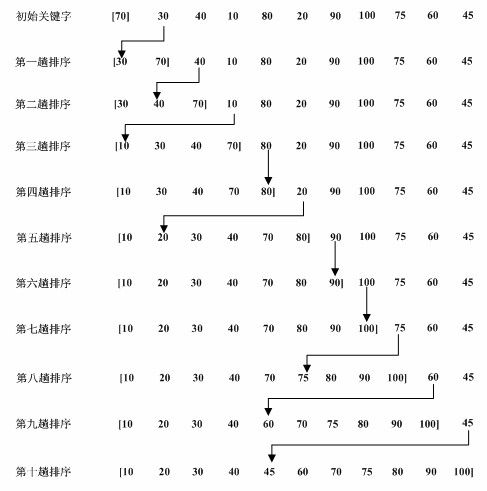
插入排序方法分直接插入排序和折半插入排序两种,下图是直接插入排序的例子
如果目标是把n个元素的序列按序排列,那么采用插入排序存在最好情况和最坏情况。最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需(n-1)次即可。最坏情况就是,序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数减去(n-1)次。平均来说插入排序算法复杂度为O(n²)。因而,插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,例如,量级小于千,那么插入排序还是一个不错的选择。
折半插入排序(binary insertion sort)
折半插入排序(binary insertion sort)是对插入排序算法的一种改进,由于排序算法过程中,就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列,这样我们不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度。
折半插入排序算法是一种稳定的排序算法,比直接插入算法明显减少了关键字之间比较的次数,因此速度比直接插入排序算法快,但记录移动的次数没有变,所以折半插入排序算法的时间复杂度仍然为O(n^2),与直接插入排序算法相同。
#include <stdio.h>
#include <stdlib.h>
void binary_insert_sort(int a[], int len) {
int key,i, j,low, high, mid;
for(i = 1; i < len; i++) {
if(a[i] < a[i-1]) {
low = 0;
high = i - 1;
key = a[i];
while(low <= high) {
mid = (low + high) / 2;
if(key < a[mid])
high = mid - 1;
else
low = mid + 1;
}
for(j = i; j > high + 1; j--)
a[j] = a[j - 1];
a[high + 1] = key;
}
}
}
int main(int argc, const char *argv[]) {
int i;
int tiny[] = {4, 9,7, 13, 0, 14, 2, 12, 8, 5};
binary_insert_sort(tiny, 10);
for(i = 0; i < 10; i++) {
printf("%d ", tiny[i]);
}
return 0;
}
§2 希尔排序(shell sort)算法
希尔排序(Shell Sort)
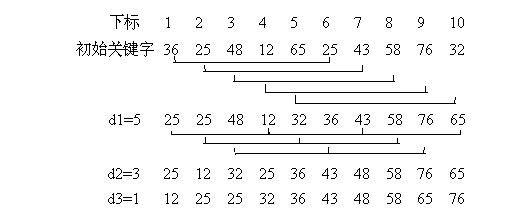
希尔排序(Shell Sort)又称为“缩小增量排序”。该方法的基本思想是:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序在对几乎已经排好序的数据操作时, 效率高, 即可以达到线性排序的效率
但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位
步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。
#include <stdio.h>
void output_array(int data[], int n)
{
int i;
for(i = 0; i < n; i++)
printf("%d ", data[i]);
printf("\n");
}
void swap(int *a, int *b)
{
int x;
x = *a;
*a = *b;
*b = x;
}
void insertion_sort(int data[], int n, int increment)
{
int i, j;
for(i = increment; i < n; i += increment)
for(j = i; j >= increment && data[j] > data[j - increment]; j -= increment)
swap(&data[j], &data[j - increment]);
}
void shellsort(int data[], int n)
{
int i, j;
for(i = n / 2; i > 2; i /= 2)
for(j = 0; j < i; j++)
insertion_sort(data + j, n - j, i);
insertion_sort(data, n, 1);
}
int main()
{
int data[] = {5, 3, 1, 665, 77, 66, 44, 11, 10, 9, 8, 6};
output_array(data, 12);
shellsort(data, 12);
output_array(data, 12);
return 0;
}
§3 图书馆排序(library sort)算法
图书馆(Library Sort)
图书馆(Library Sort)基于折半查找的插入排序,插入时在元素附近空出一定位置,这样推入后移动元素的复杂度由原来的O(n)下降为平均O(1),于是整个算法的复杂度达到O(nlogn)。当输入正序或倒序时,插入点都在同一位置,“留空位”的策略失效,这时就出现最坏复杂度O(n^2)。
特色:Library sort优于传统的插入排序(时间复杂度为O(n^2)),它的时间复杂度为O(nlogn),采用了空间换时间的策略。
思想:一个图书管理员需要按照字母顺序放置书本,当在书本之间留有一定空隙时,一本新书上架将无需移动随后的书本,可以直接插空隙。Library sort的思想就源于此。
实现:有n个元素待排序,这些元素被插入到拥有(1+e)n个元素的数组中。每次插入2^(i-1)个元素,总共需要插logn趟。这2^(i-1)个元 素将被折半插入到已有的2^(i-1)个元素中。因此,插入i趟之后,已有2^i个元素插入数组中。此时,执行rebalance操作,原有处在(1+ e)2^i个位置的元素将被扩展到(2+2e)2^i个位置。这样,在做插入时,由于存在gap,因此在gap未满之前无需移动元素。
#include <cstdio>
#include <cstdlib>
#include <ctime>
static unsigned int set_times = 0;
static unsigned int cmp_times = 0;
template<typename item_type> void setval(item_type& item1, item_type& item2) {
set_times += 1;
item1 = item2;
return;
}
template<typename item_type> int compare(item_type& item1, item_type& item2) {
cmp_times += 1;
return item1 < item2;
}
template<typename item_type> void swap(item_type& item1, item_type& item2) {
item_type item3;
setval(item3, item1);
setval(item1, item2);
setval(item2, item3);
return;
}
template<typename item_type> void library_sort(item_type* array, int size) {
item_type* bucket = new item_type[size * 3];
int* filled = new int[size * 3];
int i;
int l;
int m;
int r;
int ins_pos;
int bucket_size;
item_type tempitem;
if(size > 0) {
for(i = 1; i < size * 3; i++) {
filled[i] = 0;
}
filled[0] = 1;
bucket[0] = array[0];
bucket_size = 1;
}
for(i = 1; i < size; i++) {
l = 0;
r = bucket_size - 1;
while(l <= r) {
m = (l + r) / 2;
compare(array[i], bucket[m * 3]) ? r = m - 1 : l = m + 1;
}
ins_pos = (r >= 0) ? r * 3 + 1 : 0;
setval(tempitem, array[i]);
while(filled[ins_pos]) {
if(compare(tempitem, bucket[ins_pos])) {
swap(bucket[ins_pos], tempitem);
}
ins_pos++;
}
setval(bucket[ins_pos], tempitem);
filled[ins_pos] = 1;
if(i == bucket_size * 2 - 1) {
r = bucket_size * 6 - 3;
l = bucket_size * 4 - 3;
while(l >= 0) {
if(filled[l]) {
filled[l] = 0;
filled[r] = 1;
setval(bucket[r], bucket[l]);
r -= 3;
}
l -= 1;
}
bucket_size = i + 1;
}
}
for(i = 0, l = 0; l < size * 3; l++) {
if(filled[l]) {
setval(array[i++], bucket[l]);
}
}
return;
}
int main(int argc, char** argv) {
int capacity = 0;
int size = 0;
int i;
clock_t clock1;
clock_t clock2;
double data;
double* array = NULL;
// generate randomized test case
while(scanf("%lf", &data) == 1) {
if(size == capacity) {
capacity = (size + 1) * 2;
array = (double*)realloc(array, capacity * sizeof(double));
}
array[size++] = data;
}
// sort
clock1 = clock();
library_sort(array, size);
clock2 = clock();
// output test result
fprintf(stderr, "library_sort:\t");
fprintf(stderr, "time %.2lf\t", (double)(clock2 - clock1) / CLOCKS_PER_SEC);
fprintf(stderr, "cmp_per_elem %.2lf\t", (double)cmp_times / size);
fprintf(stderr, "set_per_elem %.2lf\n", (double)set_times / size);
for(i = 0; i < size; i++) {
fprintf(stdout, "%lf\n", array[i]);
}
free(array);
return 0;
}
§4 耐心排序(patience sort)算法
耐心排序(Patience Sorting)
这个排序的关键在建桶和入桶规则上
建桶规则:如果没有桶,新建一个桶;如果不符合入桶规则那么新建一个桶
入桶规则:只要比桶里最上边的数字小即可入桶,如果有多个桶可入,那么按照从左到右的顺序入桶即可
举个例子,待排数组[6 4 5 1 8 7 2 3]
第一步,取数字6出来,此时一个桶没有,根据建桶规则1新建桶,将把自己放进去,为了表述方便该桶命名为桶1或者1号桶
第二步,取数字4出来,由于4符合桶1的入桶规则,所以入桶1,并放置在6上边,如下图2所示
第三步,取数字5出来,由于5不符合桶1的入桶规则,比桶1里最上边的数字大,此时又没有其它桶,那么根据建桶规则新建桶2,放入住该桶
第四步,取数字1出来,1即符合入1号桶的规则,比4小嘛,也符合入2号桶的规则,比5也小,两个都可以入,根据入桶规则1入住1号桶(实际入住2号桶也没关系)
第五步,取数字8出来,8比1号桶的掌门1大,比2号桶的掌门5也大,而且就这俩桶,所以8决定自立门派,建立了3号桶,并入住该桶成为首位掌门
第六步,取数字7出来,1号桶,2号桶的掌门都不行,最后被3号桶收服,投奔了3号桶的门下
第七步,取数字2出来,被2号桶掌门收了
第八步,取数字3出来,被3号桶的现任掌门7收了
全部入桶完毕。
然后从第一个桶顺序取出数字1 4 6,2 5,3 7 8,然后再次进行插入排序,其实也是对插入排序的改进,不过这个改进对与求解连续递增子序列问题还是很便利,很直观。
#include <vector>
#include <algorithm>
#include <stack>
#include <iterator>
template<typename PileType>
bool pile_less(const PileType& x, const PileType& y)
{
return x.top() < y.top();
}
// reverse less predicate to turn max-heap into min-heap
template<typename PileType>
bool pile_more(const PileType& x, const PileType& y)
{
return pile_less(y, x);
}
template<typename Iterator>
void patience_sort(Iterator begin, Iterator end)
{
typedef typename std::iterator_traits<Iterator>::value_type DataType;
typedef std::stack<DataType> PileType;
std::vector<PileType> piles;
for (Iterator it = begin; it != end; it++)
{
PileType new_pile;
new_pile.push(*it);
typename std::vector<PileType>::iterator insert_it =
std::lower_bound(piles.begin(), piles.end(), new_pile,
pile_less<PileType>);
if (insert_it == piles.end())
piles.push_back(new_pile);
else
insert_it->push(*it);
}
// sorted array already satisfies heap property for min-heap
for (Iterator it = begin; it != end; it++)
{
std::pop_heap(piles.begin(), piles.end(), pile_more<PileType>);
*it = piles.back().top();
piles.back().pop();
if (piles.back().empty())
piles.pop_back();
else
std::push_heap(piles.begin(), piles.end(), pile_more<PileType>);
}
}
§5 小结
这篇博文对插入排序进行了全面的介绍,虽然讲解的相对简单,一方面是由于本身理论相对简单(直接插入排序算法),另一方面是由于理论还不确定(希尔排序算法的算法复杂度分析),还有就是理论相对较新颖,但还是通过实例图解和代码实现还是可以有一个不错的理解。如果你有任何建议或者批评和补充,请留言指出,不胜感激,更多参考请移步互联网。
参考:
①jxva: http://www.jxva.com/blog/201204/400.html
②银河使者: http://www.cnblogs.com/nokiaguy/archive/2008/05/16/1199359.html
③RichSelian: http://www.cnblogs.com/richselian/archive/2011/09/16/2179152.html
④zhangyu8374: http://zhangyu8374.iteye.com/blog/86317
⑤kkun: http://www.cnblogs.com/kkun/archive/2011/11/23/2260291.html
⑥更多资料参考——维基百科