1. A total order is a binary relation ≤ that satisfies
a) Antisymmetry: if v ≤ w and w ≤ v, then v = w.
b) Transitivity: if v ≤ w and w ≤ x, then v ≤ x.
c) Totality: either v ≤ w or w ≤ v or both.
2. Comparable API: Implement compareTo() so that v.compareTo(w)
a) Is a total order.
b) Returns a negative integer, zero, or positive integer if v is less than, equal to, or greater than w, respectively.
c) Throws an exception if incompatible types (or either is null).
3. Built-in comparable types. Integer, Double, String, Date, File, ...
4. Test if an array is sorted:
private static boolean isSorted(Comparable[] a)
{
for (int i = 1; i < a.length; i++)
if (less(a[i], a[i-1])) return false;
return true;
}
If the sorting algorithm passes the test, it doesn't mean that it correctly sort the array, we need to check whether each elements in the original array is still in the sorted array. ( i.e. the algorithm can return an arry with all zero.
5. Selection sort :
a) In iteration i, find index min of the smallest entry in the remaining ones.
b) Swap a[i] and a[min].
int N = a.length;
for (int i = 0; i < N; i++)
{
int min = i;
for (int j = i+1; j < N; j++)
if (less(a[j], a[min]))
min = j;
exch(a, i, min);
}
6. Selection sort uses (N – 1) + (N – 2) + ... + 1 + 0 ~ N^2 / 2 compares and N exchanges. Running time is insensitive to input. Quadratic time, even if input is sorted. Data movement is minimal. Linear number of exchanges.
7. Insertion sort :
a) In iteration i, swap a[i] with each larger entry to its left.
int N = a.length;
for (int i = 0; i < N; i++)
for (int j = i; j > 0; j--)
if (less(a[j], a[j-1]))
exch(a, j, j-1);
else break;
8. Proposition: To sort a randomly-ordered array with distinct keys, insertion sort uses ~ ¼ N^2 compares and ~ ¼ N^2 exchanges on average. Pf: Expect each entry to move halfway back.
9. An inversion is a pair of keys that are out of order. An array is partially sorted if the number of inversions is ≤ c N.
a) Ex 1. A subarray of size 10 appended to a sorted subarray of size N.
b) Ex 2. An array of size N with only 10 entries out of place.
10. Proposition: For partially-sorted arrays, insertion sort runs in linear time. Pf: Number of exchanges equals the number of inversions.
11. Shell sort : h-sort array for decreasing sequence of values of h.
a) Big increments ⇒ small subarray.
b) Small increments ⇒ nearly in order.
12. A g-sorted array remains g-sorted after h-sorting it.
int N = a.length;
int h = 1;
while (h < N/3) h = 3*h + 1; // 1, 4, 13, 40, 121, 364, ...
while (h >= 1)
{ // h-sort the array.
for (int i = h; i < N; i++)
{
for (int j = i; j >= h && less(a[j], a[j-h]); j -= h)
exch(a, j, j-h);
}
h = h/3;
}
13. Shuffle sort :
a) Generate a random real number for each array entry.
b) Sort the array.
Shuffle sort produces a uniformly random permutation of the input array, provided no duplicate values.
14. Knuth shuffle :
a) In iteration i, pick integer r between 0 and i uniformly at random.
b) Swap a[i] and a[r].
Knuth shuffling algorithm produces a uniformly random permutation of the input array in linear time.
int N = a.length;
for (int i = 0; i < N; i++)
{
int r = StdRandom.uniform(i + 1);
exch(a, i, r);
}
15. The convex hull of a set of N points is the smallest perimeter fence enclosing the points. Equivalent definitions:
a) Smallest convex set containing all the points.
b) Smallest area convex polygon enclosing the points.
c) Convex polygon enclosing the points, whose vertices are points in set.
Convex hull output: Sequence of vertices in counterclockwise order.
16. Convex hull application:
a) Find shortest path in the plane from s to t that avoids a polygonal obstacle. Shortest path is either straight line from s to t or it is one of two polygonal chains of convex hull.
b) Given N points in the plane, find a pair of points with the largest Euclidean distance between them. Farthest pair of points are extreme points on convex hull.
17. Fact of convex hull :
a) Can traverse the convex hull by making only counterclockwise turns.
b) The vertices of convex hull appear in increasing order of polar angle with respect to point p with lowest y-coordinate.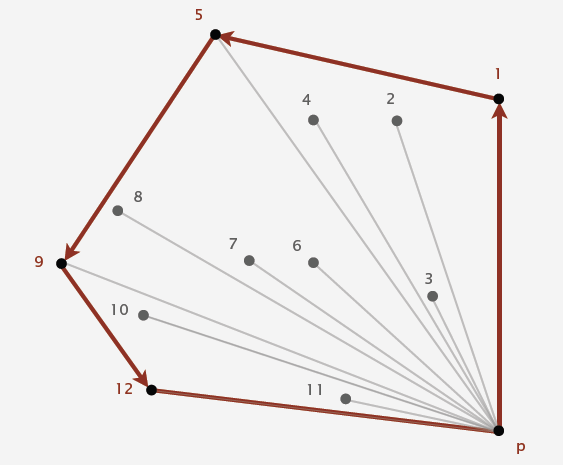
18. Graham scan :
a) Choose point p with smallest y-coordinate.
b) Sort points by polar angle with p.
c) Consider points in order; discard unless it create a ccw turn.
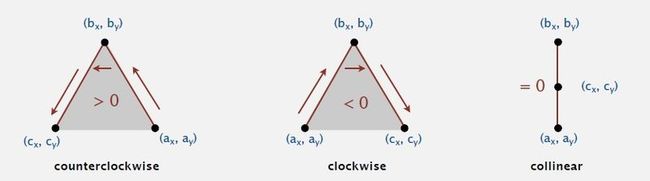
19. Given three points a, b, and c, is a → b → c a counterclockwise turn?
a) Determinant (or cross product) gives 2x signed area of planar triangle.

b) If signed area > 0, then a → b → c is counterclockwise.
c) If signed area < 0, then a → b → c is clockwise.
d) If signed area = 0, then a → b → c are collinear.
20. Polar order:
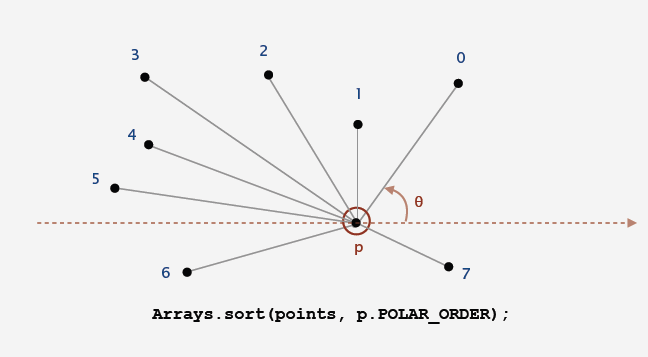
A ccw-based solution.
a) If q1 is above p and q2 is below p, then q1 makes smaller polar angle.
b) If q1 is below p and q2 is above p, then q1 makes larger polar angle.
c) Otherwise, ccw(p, q1, q2) identifies which of q1 or q2 makes larger polar angle.
private class PolarOrder implements Comparator<Point2D>
{
public int compare(Point2D q1, Point2D q2)
{
double dx1 = q1.x - x;
double dy1 = q1.y - y;
if (dy1 == 0 && dy2 == 0) { ... }
else if (dy1 >= 0 && dy2 < 0) return -1;
else if (dy2 >= 0 && dy1 < 0) return +1;
else return -ccw(Point2D.this, q1, q2);
}
}