1. Informal Goal: Connect a bunch of points together as cheaply as possible.
Blazingly Fast Greedy Algorithms:
- Prim's Algorithm
- Kruskal's algorithm
O(m log n) m is the # of edges and n is the # of vertices.
2. Problem Denition:
Input: Undirected graph G = ( V , E ) and a cost ce for each edge e in E.
- Assume adjacency list representation
- OK if edge costs are negative
Output: minimum cost ( sum of edge costs) tree T contained by E that spans all vertices .
Definition of spanning tree:
a) T has no cycles
b) The subgraph (V,T) is connected (i.e., contains path between each pair of vertices)
3. Standing Assumptions:
Assumption #1: Input graph G is connected.
- Else no spanning trees.
- Easy to check in preprocessing (e.g., depth-rst search).
Assumption #2: Edge costs are distinct.
- Prim + Kruskal remain correct with ties (which can be broken arbitrarily).
- Correctness proof a bit more annoying.
4. Prim's MST Algorithm:
- Initialize X = {s} [s in V chosen arbitrarily]
- T = empty set [invariant: X = vertices spanned by tree-so-far T]
- While X <> V
- Let e = (u, v) be the cheapest edge of G with u in X, v not in X.
- Add e to T
- Add v to X.
While loop: Increase # of spanned vertices in cheapest way possible.
5. Denition of Cut : A cut of a graph G = (V , E) is a partition of V into 2 non-empty sets. ( at most 2^(n-1) -1 cuts)
6. Empty Cut Lemma: A graph is not connected <==> exists a cut (A , B) with no crossing edges.
Proof : <== choose u in A and v in B , there is no path from u to v.
==> for (u, v) in G, that there is no path from u to v, Define :
A = {Vertices reachable from u in G}
B = V - A
So, no edge from A to B, otherwise A will be bigger
7. Double-Crossing Lemma: Suppose the cycle C in E has an edge crossing the cut (A , B): then so does some other edge of C. ( the crossing edge of C should be even)
8. Lonely Cut Corollary: If e is the only edge crossing some cut (A , B), then it is not in any cycle.
9. Claim: Prim's algorithm outputs a spanning tree.
Proof: (1) Algorithm maintains invariant that T spans X
(2) Can't get stuck with X <> V (other wise cut {X, V-X} has no crossing edge ==> G is disconnected
(3) No cycles ever get created in T. A newly added edge e is the 1st edge crossing (X , V - X) that gets added to T ==> its addition can't create a cycle in T
10. Cut Property: Consider an edge e of G. Suppose there is a cut (A , B) such that e is the cheapest
edge of G that crosses it. Then e belongs to the MST of G.
Proof : Suppose there is an edge e that is the cheapest one crossing a cut (A , B), yet e is not in the MST T*.
Idea: Exchange e with another edge in T* to make it even cheaper(contradiction).
Since T* is connected, must construct an edge f (<> e) crossing (A , B).
However exchange f with e may make T* not a spanning tree :
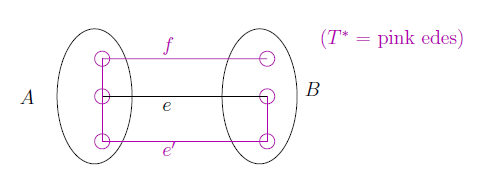
How to find e' : Let C = cycle created by adding e to T*. ( there is already path between the nodes connected by e, so adding e to T* constructs a cycle)
By the Double-Crossing Lemma: Some other edge e' of C [with e' <> e and e' in T] crosses (A , B).
T = T * U {e} - {e'} is also a spanning tree. Since ce < ce' , T cheaper than purported MST T*
11. Claim: Cut Property ==> Prim's algorithm is correct.
Proof: By previous video, Prim's algorithm outputs a spanning tree T*.
Key point: Every edge e in T* is explicitly justied by the Cut Property.
==> T* is a subset of the MST
==> Since T* is already a spanning tree, it must be the MST
12. Running time of straightforward implementation:
- O(n) iterations [where n = # of vertices]
- O(m) time per iteration [where m = # of edges]
==> O(mn) time
13. Prim's Algorithm with Heaps:
Invariant #1: Elements in heap = vertices of V - X.
Invariant #2: For v in V - X, key[v] = cheapest edge (u , v) with u in X (or infinitive if no such edges exist).
Given invariants, Extract-Min yields next vertex v not in X and edge (u , v) crossing (X , V - X) to add to X and T, respectively.
Can initialize heap with O( m + n log n ) = O(m log n) preprocessing. Inserts m >= n - 1 since G connected.
Pseudocode: When v added to X:
- For each edge (v , w) in E:
- If w in V - X ==> The only whose key might have changed (Update key if needed:)
- Delete w from heap
- Recompute key[w]:=min{key[w],cvw}
- Re-Insert into heap
14. Running Time with Heaps :
- Dominated by time required for heap operations
- (n - 1) Inserts during preprocessing
- (n - 1) Extract-Mins (one per iteration of while loop)
- Each edge (v , w) triggers one Delete/Insert combo
[When its 1rst endpoint is sucked into X]
==> O(m) heap operations [ m >= n - 1 since G connected]
==> O(m log n) time [As fast as sorting!]