前言
InsersionSort是一种很简单直观的排序方法。它本身的过程类似于我们我们玩扑克牌的时候一张张的从后面往前的调整顺序。而归并排序是另外一种典型思想的应用,divide and conquer。从表面上看起来,他们两者的联系也就在于都是排序的方法而已。如果这个时候我们把它们和常用的一个数学概念逆序联系起来,会发现他们之间有一些比较有意思的东西。
InsertionSort介绍
插入排序的过程非常简单,用通俗的语言来描述的话,则是如下的一个过程:
1. 从第二个元素开始向前比较,一直到最后一个元素。
2. 在比较的过程中,如果前面的元素比当前元素大,则将前面的元素往后面移动一位。这样直到一个元素,将目标元素放置进去。
因为整体过程比较简单,这里我们不作详细的描述。
一个参考的实现代码如下:
public static void sort(int[] a)
{
for(int i = 1; i < a.length; i++)
{
int key = a[i];
int j = i - 1;
while(j >= 0 && a[j] > key)
{
a[j + 1] = a[j];
j--;
}
a[j + 1] = key;
}
}
这里的一个比较元素和放置的方式是将当前需要参加比较的元素放到一个key元素里,然后每次比较的时候直接将前面大的元素覆盖后面的元素。这样直到循环外面的时候将key放置进去。还有一种实现的方式就是每次发现前面元素比较大的时候就直接和前面元素交换位置。这两者实现的最终结果是一样的。
总的来说,这个排序方法的实现没什么特殊的。我们这里的介绍相当于先埋下一个伏笔。
逆序的概念
我们现在来看看逆序的概念。一般来说,如果我们有这么一个数组a[n]。在这个数组里,则一般元素排列的位置i, j表示它们所在的索引位置。如果对于i < j这两个元素,a[i] > a[j],则表示它们两个构成一个逆序。
我们来看一个例子,比如说我们有数组{2, 3, 8, 6, 1}。 对于第一个元素2来说,排在它后面的元素而且比它还小的就和它构成了一个逆序。比如2和1。3和1, 8 和6以及1都构成逆序关系。这样,我们就很自然的会引申出一个问题,如果我们需要计算一个数组里所有逆序的关系,有什么好的办法吗?
统计法
第一个我们所能想到的方法就是前面按照定义所说明的过程。既然我们每个逆序都是一个前面元素比后面元素大,那么我们就从数组的开头每个元素向后比较,如果比当前元素小,就算累加一个逆序。这样我们可以得到一个很简单的方法:
public static int inversion(int[] a) {
int count = 0;
for(int i = 0; i < a.length - 1; i++) {
for(int j = i + 1; j < a.length; j++) {
if(a[i] > a[j])
count++;
}
}
return count;
}
从算法的时间复杂度来说,它的复杂度达到了o(n^2)。
除了这个方法外,我们还有其他的办法吗?我们再看看另外一个思路。
Insersion sort
现在我们再来回顾前面insersion sort的过程。每次一个元素都要和前面进行比较,如果前面的元素比当前元素大,他们就要交换位置。而前面的元素比当前元素,这不正说明他们构成了一个逆序吗?而我们交换他们的位置就消除了一个逆序。如此看来我们排序的过程就是一个消除逆序的过程。而且我们再来看,我们这个元素和前面的元素比较,他们交换位置之后并不会影响到数组后面的元素和前面元素的逆序关系。所以,我们只要把insersion sort里交换的次数统计出来就知道有多少个逆序了。按照这种思路,我们得到另外一种实现代码:
public static int inversion(int[] a)
{
int count = 0;
for(int i = 1; i < a.length; i++)
{
int key = a[i];
int j = i - 1;
while(j >= 0 && a[j] > key)
{
a[j + 1] = a[j];
j--;
count++;
}
a[j + 1] = key;
}
return count;
}
从前面对insersion sort的讨论知道,它的时间复杂度也是o(n^2)。看来这里只是体现了一种思路,但是算法性能上并没有什么改进。那么,我们还有没有更好的改进呢?
归并排序
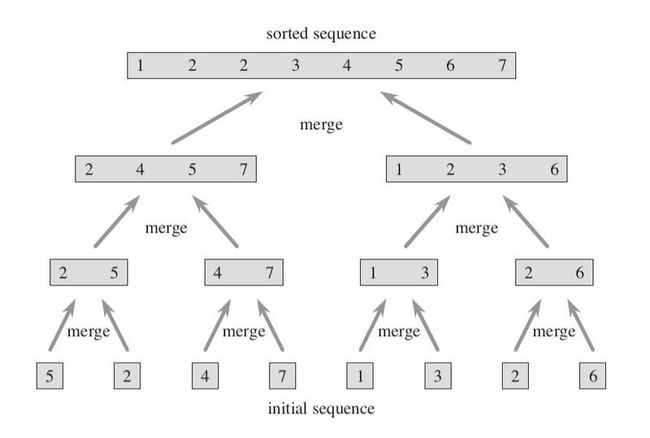
归并排序的过程主要是一种分治的思想。它首先将数组分解成两个部分,然后分别对每个部分进行排序。通过这么一个不断递归细分的过程达到排序的效果。一个典型的过程如下图:
这里只是展示了整体的排序过程。可是他们和逆序有什么关系呢?考虑到前面我们提到过,排序就是消除逆序的过程。如果每个独立的过程对逆序的计算不影响全局的话,我们可以有一个法子来处理。我们知道,在归并排序里,消除这些逆序的过程就在于merge这个步骤。而merge这里是要合并两个排好序的数组。在前面的示例里我们可以看到一个这样的场景,比如说当我们要归并数组[2, 4, 5, 7]和[1, 2, 3, 6]时。一旦前面的某个元素比后面元素大,则从该元素起到该子数组里所有的元素都和后面的元素构成逆序。而如果我们把后面的元素放入到合并后的数组中时,这些逆序都被消除了。注意到的是,这里消除的是若干个逆序而不止一个。比如说前面2, 4, 5, 7和后面数组里的1就构成了4个逆序,如果把1放到贵并的结果数组中,这些逆序就消除了。
因此,有了这些讨论之后,我们就知道该怎么来计算逆序了。只要在每次归并的时候看后面和前面元素的比较,如果后面的元素比前面元素小,则增加前面数组所有剩下元素的个数作为增加的逆序数。一个根据归并排序的修改版逆序统计方法就出来了:
public static void mergeSort(int[] array, int start, int end)
{
if(start < end)
{
int middle = start + (end - start) / 2;
mergeSort(array, start, middle);
mergeSort(array, middle + 1, end);
merge(array, start, middle, end);
}
}
public static void merge(int[] a, int start, int middle, int end)
{
int[] array = new int[end - start + 1];
int i = 0, j = start, k = middle + 1;
while(j <= middle && k <= end)
{
if(a[j] <= a[k])
array[i++] = a[j++];
else
{
count += middle - j + 1;
array[i++] = a[k++];
}
}
while(j <= middle)
array[i++] = a[j++];
while(k <= end)
array[i++] = a[k++];
for(i = 0; i < array.length; i++)
a[start + i] = array[i];
}
要注意到的一点就是,这里几乎和归并排序的代码一样,就是在里面增加了一行: count += middle - j + 1; 这里的count我们可以在具体实现的程序里定义成一个全局的静态变量。后面只需要取这个变量就可以了。
我们从归并排序的特性说明可以知道,该算法的时间复杂度为O(nlgn)。
总结
求逆序和排序算法有着比较紧密的联系。我们排序就是一个消除逆序的过程。对于这个话题在一年前的时候就已经想讨论一番了。因为除了前面的这几种方法以外还有一种比较巧妙的办法。可惜一直没有时间去体会也没有参透。等以后有时间的时候再好好的补充总结一下。
参考材料
http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=binaryIndexedTrees