算法 之 分治 - 快速排序
这篇文章介绍 一个非常流行并且高效的排序算法:QuickSort。
该算法优于 MergeSort 的一点是它在原位上排序,即对于被排序的元素,不需要辅助的存储空间。
在介绍 QuickSort 之前,需要先介绍划分算法,它是 QuickSort 的基础。
1. Split
设 A[low...high] 是一个包含 n 个数的数组,并且 x = A[low]。我们考虑重新安排数组 A 中的元素的问题,使得小于或等于 x 的元素在 x 的前面,随后 x 又在所有大于它的元素的前面。
经过数组中的元素改变排列后,对于某个 w,low ≤ w ≤ high,x 在 A[w] 中。
例如,假设 A = { 5, 3, 9, 2, 7, 1, 8 },low = 1,high = 7,则经过重新排列其中的元素后,得到 A = { 1, 3, 2, 5, 7, 9, 8 },这样元素重新排列后,w = 4.这种重排列行动也称为围绕 x 的拆分或划分,x 称为主元或拆分元素。
如果元素 A[j] 既不小于 A[low...j-1] 中的元素,也不大于 A[j+1...high]中的元素,则称其处在一个适当位置或正确位置。
用 x (x ∈ A) 作为主元划分数组 A 后,x 将处于一个正确位置。
过程 Split
输入 数组 A[low...high]
输出 (1) 如果有必要,输出重新排列的数组 A
(2) 划分元素 A[low] 的新位置 w
算法描述
i ← low
x ← A[low]
for j ← low + 1 to high
if A[j] ≤ x then
i ← i + 1
if i ≠ j then 互换 A[i] 和 A[j]
end if
end for
互换 A[low] 和 A[i]
w ← i
return A 和 w
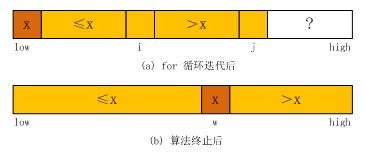
整个算法的执行过程中,始终保持两个索引 i 和 j,并在初始时分别设置为 low 和 low + 1,这两个索引从左向右移动,使得经过每个 for 循环迭代后,有:
(1) A[low] = x
(2) A[k] ≤ x,对于所有 k,low ≤ k ≤ i
(3) A[k] > x,对于所有 k,i < k ≤ j
算法对所有元素扫描后,用 A[i] 与主元交换,这样所有小于或等于主元的元素处在它的左边,并且所有大于主元的元素落在它的右边。
private static int split(int[] array, int low, int high)
{
int splitIndex = low;
int lowValue = array[low];
for (int i = low + 1; i <= high; i++)
{
if (array[i] > lowValue)
continue;
splitIndex++;
if (splitIndex != i)
{
array[splitIndex] = array[splitIndex] + array[i];
array[i] = array[splitIndex] - array[i];
array[splitIndex] = array[splitIndex] - array[i];
}
}
if (low != splitIndex)
{
array[low] = array[low] + array[splitIndex];
array[splitIndex] = array[low] - array[splitIndex];
array[low] = array[low] - array[splitIndex];
}
return splitIndex;
}
2. QuickSort
算法 QuickSort 在它的最简单的形式中能概括如下:
要排序的元素 A[low...high] 通过算法 Split 重新排列元素,使得原先在 A[low] 中的主元占据其正确的位置 A[w],并且所有小于或等于 A[w] 的元素所处的位置为 A[low...w-1],而所有大于 A[w] 的元素所处的位置是 A[w+1...high]。
子数组 A[low...w-1] 和 A[w+1...high] 递归地排序,产生整个排序数组。
过程 QuickSort
输入 n 个元素的数组 A[1...n]
输出 按非降序排列的数组 A
算法描述 quickSort(A, low, high)
if low < high then
w ← Split(A, low, high) { w 为 A[low] 的新位置}
quickSort(A, low, w-1)
quickSort(A, w+1, high)
end if
public static void quickSort(int[] array, int low, int high)
{
if (low > high)
return;
int splitIndex = split(array, low, high);
quickSort(array, low, splitIndex - 1);
quickSort(array, splitIndex + 1, high);
}