一致性hash算法 - consistent hashing
一致性hash算法(consistent hashing)
张亮
consistent hashing算法早在1997年就在论文Consistent hashing and random trees中被提出,目前在cache系统中应用越来越广泛;
1基本场景
比如你有N个cache服务器(后面简称cache),那么如何将一个对象object映射到N个cache上呢,你很可能会采用类似下面的通用方法计算object的hash值,然后均匀的映射到到N个cache;
hash(object)%N
一切都运行正常,再考虑如下的两种情况;
1一个cache服务器m down掉了(在实际应用中必须要考虑这种情况),这样所有映射到cache m的对象都会失效,怎么办,需要把cache m从cache中移除,这时候cache是N-1台,映射公式变成了hash(object)%(N-1);
2由于访问加重,需要添加cache,这时候cache是N+1台,映射公式变成了hash(object)%(N+1);
1和2意味着什么?这意味着突然之间几乎所有的cache都失效了。对于服务器而言,这是一场灾难,洪水般的访问都会直接冲向后台服务器;
再来考虑第三个问题,由于硬件能力越来越强,你可能想让后面添加的节点多做点活,显然上面的hash算法也做不到。
有什么方法可以改变这个状况呢,这就是consistent hashing...
2 hash算法和单调性
Hash算法的一个衡量指标是单调性(Monotonicity),定义如下:
单调性是指如果已经有一些内容通过哈希分派到了相应的缓冲中,又有新的缓冲加入到系统中。哈希的结果应能够保证原有已分配的内容可以被映射到新的缓冲中去,而不会被映射到旧的缓冲集合中的其他缓冲区。
容易看到,上面的简单hash算法hash(object)%N难以满足单调性要求。
3 consistent hashing算法的原理
consistent hashing是一种hash算法,简单的说,在移除/添加一个cache时,它能够尽可能小的改变已存在key映射关系,尽可能的满足单调性的要求。
下面就来按照5个步骤简单讲讲consistent hashing算法的基本原理。
3.1环形hash空间
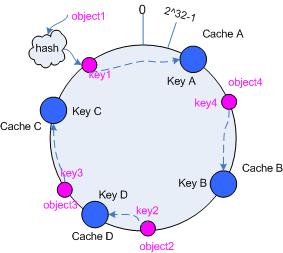
考虑通常的hash算法都是将value映射到一个32为的key值,也即是0~2^32-1次方的数值空间;我们可以将这个空间想象成一个首(0)尾(2^32-1)相接的圆环,如下面图1所示的那样。
图1环形hash空间
3.2把对象映射到hash空间
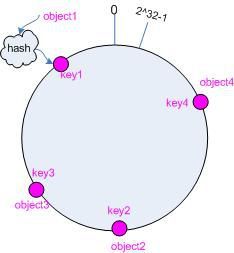
接下来考虑4个对象object1~object4,通过hash函数计算出的hash值key在环上的分布如图2所示。
hash(object1) = key1;
… …
hash(object4) = key4;
图2 4个对象的key值分布
3.3把cache映射到hash空间
Consistent hashing的基本思想就是将对象和cache都映射到同一个hash数值空间中,并且使用相同的hash算法。
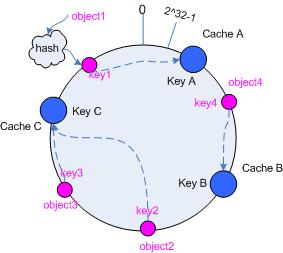
假设当前有A,B和C共3台cache,那么其映射结果将如图3所示,他们在hash空间中,以对应的hash值排列。
hash(cache A) = key A;
… …
hash(cache C) = key C;
图3 cache和对象的key值分布
说到这里,顺便提一下cache的hash计算,一般的方法可以使用cache机器的IP地址或者机器名作为hash输入。
3.4把对象映射到cache
现在cache和对象都已经通过同一个hash算法映射到hash数值空间中了,接下来要考虑的就是如何将对象映射到cache上面了。
在这个环形空间中,如果沿着顺时针方向从对象的key值出发,直到遇见一个cache,那么就将该对象存储在这个cache上,因为对象和cache的hash值是固定的,因此这个cache必然是唯一和确定的。这样不就找到了对象和cache的映射方法了吗?!
依然继续上面的例子(参见图3),那么根据上面的方法,对象object1将被存储到cache A上;object2和object3对应到cache C;object4对应到cache B;
3.5考察cache的变动
前面讲过,通过hash然后求余的方法带来的最大问题就在于不能满足单调性,当cache有所变动时,cache会失效,进而对后台服务器造成巨大的冲击,现在就来分析分析consistent hashing算法。
3.5.1移除cache
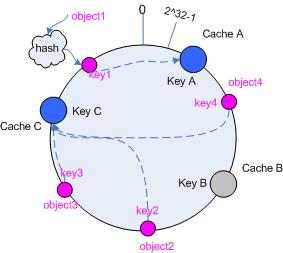
考虑假设cache B挂掉了,根据上面讲到的映射方法,这时受影响的将仅是那些沿cache B逆时针遍历直到下一个cache(cache C)之间的对象,也即是本来映射到cache B上的那些对象。
因此这里仅需要变动对象object4,将其重新映射到cache C上即可;参见图4。
图4 Cache B被移除后的cache映射
3.5.2添加cache
再考虑添加一台新的cache D的情况,假设在这个环形hash空间中,cache D被映射在对象object2和object3之间。这时受影响的将仅是那些沿cache D逆时针遍历直到下一个cache(cache B)之间的对象(它们是也本来映射到cache C上对象的一部分),将这些对象重新映射到cache D上即可。
因此这里仅需要变动对象object2,将其重新映射到cache D上;参见图5。
图5添加cache D后的映射关系
4虚拟节点
考量Hash算法的另一个指标是平衡性(Balance),定义如下:
平衡性
平衡性是指哈希的结果能够尽可能分布到所有的缓冲中去,这样可以使得所有的缓冲空间都得到利用。
hash算法并不是保证绝对的平衡,如果cache较少的话,对象并不能被均匀的映射到cache上,比如在上面的例子中,仅部署cache A和cache C的情况下,在4个对象中,cache A仅存储了object1,而cache C则存储了object2、object3和object4;分布是很不均衡的。
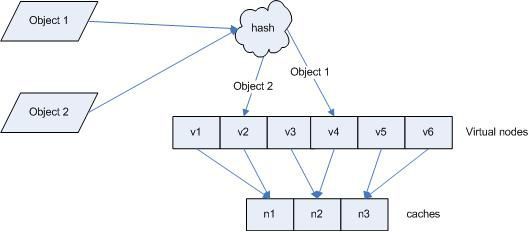
为了解决这种情况,consistent hashing引入了“虚拟节点”的概念,它可以如下定义:
“虚拟节点”(virtual node)是实际节点在hash空间的复制品(replica),一实际个节点对应了若干个“虚拟节点”,这个对应个数也成为“复制个数”,“虚拟节点”在hash空间中以hash值排列。
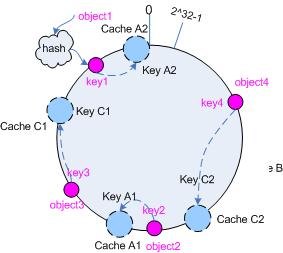
仍以仅部署cache A和cache C的情况为例,在图4中我们已经看到,cache分布并不均匀。现在我们引入虚拟节点,并设置“复制个数”为2,这就意味着一共会存在4个“虚拟节点”,cache A1, cache A2代表了cache A;cache C1, cache C2代表了cache C;假设一种比较理想的情况,参见图6。
图6引入“虚拟节点”后的映射关系
此时,对象到“虚拟节点”的映射关系为:
objec1->cache A2;objec2->cache A1;objec3->cache C1;objec4->cache C2;
因此对象object1和object2都被映射到了cache A上,而object3和object4映射到了cache C上;平衡性有了很大提高。
引入“虚拟节点”后,映射关系就从{对象->节点}转换到了{对象->虚拟节点}。查询物体所在cache时的映射关系如图7所示。
图7查询对象所在cache
“虚拟节点”的hash计算可以采用对应节点的IP地址加数字后缀的方式。例如假设cache A的IP地址为202.168.14.241。
引入“虚拟节点”前,计算cache A的hash值:
Hash(“202.168.14.241”);
引入“虚拟节点”后,计算“虚拟节”点cache A1和cache A2的hash值:
Hash(“202.168.14.241#1”);// cache A1
Hash(“202.168.14.241#2”);// cache A2
5小结
Consistent hashing的基本原理就是这些,具体的分布性等理论分析应该是很复杂的,不过一般也用不到。
http://weblogs.java.net/blog/2007/11/27/consistent-hashing上面有一个java版本的例子,可以参考。
http://blog.csdn.net/mayongzhan/archive/2009/06/25/4298834.aspx转载了一个PHP版的实现代码。
http://www.codeproject.com/KB/recipes/lib-conhash.aspxC语言版本
一些参考资料地址:
http://portal.acm.org/citation.cfm?id=258660
http://en.wikipedia.org/wiki/Consistent_hashing
http://www.spiteful.com/2008/03/17/programmers-toolbox-part-3-consistent-hashing/
http://weblogs.java.net/blog/2007/11/27/consistent-hashing
http://tech.idv2.com/2008/07/24/memcached-004/
http://blog.csdn.net/mayongzhan/archive/2009/06/25/4298834.aspx