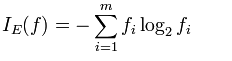Decision Tree:Analysis
大家有没有玩过猜猜看(Twenty Questions)的游戏?我在心里想一件物体,你可以用一些问题来确定我心里想的这个物体;如是不是植物?是否会飞?能游泳不?当你问完这些问题后,你就能得到这个物体的特征,然后猜出我心里想象的那个物体,看是否正确。
这个游戏很简单,但是蕴含的思想却是质朴的。每个问题都会将范围减少,直到特征显现,内蕴的思想就是Decision Tree算法。判定树(Decision Tree)算法是机器学习中很重要的一种算法,有文章声称该算法在ML学习中最为常用的算法,你不需要明白高深的知识就能明白算法的运行原理。
Decision Tree包括以下几个部分:
- Root:根节点,Decision Tree使用了树的概念,必然有Root属性。
- Decision Node:判定节点,该节点的数据会继续根据数据属性继续进行判定。
- Branch:从Decision Node迭代生成的子树是子树根节点的一个属性判断
- End Node:也称为Leaf Node,该节点实际上是做出决定的节点,对于样本属性的判断到Leaf Node结束。
Decision Tree分类:
Classification Tree:测试数据经过Classification Tree处理后,看结果归属于那个类别(Class)。
Regression Tree:如果测试数据的输出是数值类型,可以考虑使用Regression Tree。
CART(Classification And Regression Tree)s算法是对上面两种算法的术语涵盖。用来回归的树(Regression Tree)和用来分类的树(classification Tree)具有一定的相似性,不过其不同之处在于决定分裂(Split)的过程。
使用某些技术(Ensemble Methods),可以构建多个Decision Tree:
Bagging Decision Tree:创建多个Decision Tree,通过替换训练集合,得到多个Decision Tree,最终得到一致的结果。
Random Forest Classification Decision Tree:使用多个Decision Tree,提升分类的准确率。
Boosted Trees:可以使用于回归(Regression)和分类(Classification)的问题。
Rotation Forest:Decision Tree生成是从训练集合特征属性中随机选取,使用PCA分析方法来构建Decision Tree。
Gini Impurity
该Gini度量是指随机选择集合中的元素,根据集合中label的分布将该元素赋予分类,该元素分类错误的几率。Gini度量在CART算法中使用,其定义如下:
其中i为label标签,fi为label为i标签的比例(Fraction)
Information Gain
这个是比较常见的信息度量,在Information Theory中经常使用,基于熵(entropy)的概念。在ID3、C4.5、C5.0中使用。其定义如下:
i为label标签,fi为label标签的比例,和上面的定义一致。Information Gain的定义如下:
Entropy和Information Gain的定义还会在后面章节里用到,确保自己正确理解了Information Gain的定义。 本文最后会有个教程,帮助大家学习下Information Gain的概念。
Decision Tree的优点和缺点:
1:易于理解和解释,简单解释就能明白Decision Tree的模型和运行原理,对于结果也比较容易解释。
2:数据预处理少,其它算法需要处理Data Normalization、Dummy Variable、Blank Value都需要进行预处理。
3:能够处理数值数据和分类数据,能够使用Decision Tree和Regression Tree就是例证。
4:使用白盒(White Box)模型,使用白盒模型能够在给定测试数据下解释测试结果分类,NN(Neural Network)分类就难以解释,至少没有Decision Tree模型明晰。
5:易于使用统计数据验证模型,能够解释模型的可用性和可信赖度
6:健壮,数据假设比较少,该模型仅仅依赖于观察到的数据,归于数据生成模型假设比较少。
7:在大数据量情况下也能很快给出结果,根据Decision Tree抽取出来的规则能够很快的运用于测试数据,运行快速。
缺点:
1:最优Decision Tree是NP难题,所以使用的Decision-Tree算法都是基于启发式(Heuristic)算法,如Greedy Algorithm等,在每个节点判断都是根据局部最优解来进行操作。启发式算法不能保证返回全局最优的Decision Tree。
2:容易产生过于复杂的树,不能很好地获得数据的通用模型,这个实际上是被称为是Overfitting,剪枝技术能够很好的避免这个问题。
3:Decision Tree的表示能力有限,只能表示有限的数据操作,如XOR、Parity、Multiplexer等操作就不易表示;导致Decision Tree变得特别大,解决方法可以使用改变问题域的表示(Propositionalisation),或者使用更加复杂的表示方法,如Statistical Relational Learning、Inductive Logic Programming等。
4:对于包含分类变量(Categorical Variable)的数据,使用Information Gain分裂会造成较大的偏差
Extension:
Decision Tree使用And或者是Conjunction来在Decision Node进行判断,逐步得到结果;Decision Graph则是使用Or或者Disjunction来连接路径(判断条件)。在Decision Graph中,使用MML(Minimum Message length)来对Path进行处理,更细节的内容请自行查找。
关于Decision Tree的实现比较多,其中Weka中有一部分Decision Tree的经典算法实现,大家可以将weka的源码下载下来,仔细阅读下。
参考文献:
http://www.comp.lancs.ac.uk/~kc/Lecturing/csc355/DecisionTrees_given.pdf