对于很多元素为零的稀疏矩阵,仅存储非零元素可使矩阵操作效率更高。现有许多种稀疏矩阵的存储方式,但是多数采用相同的基本技术,即存储矩阵所有的非零元素到一个线性数组中,并提供辅助数组来描述原数组中非零元素的位置。
以下是几种常见的稀疏矩阵存储格式:
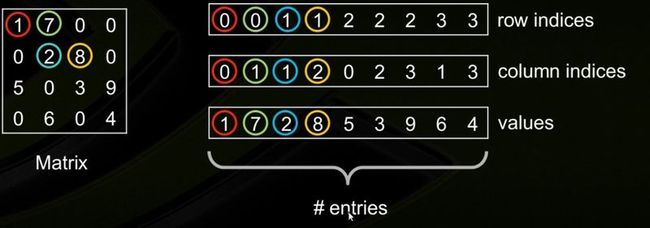
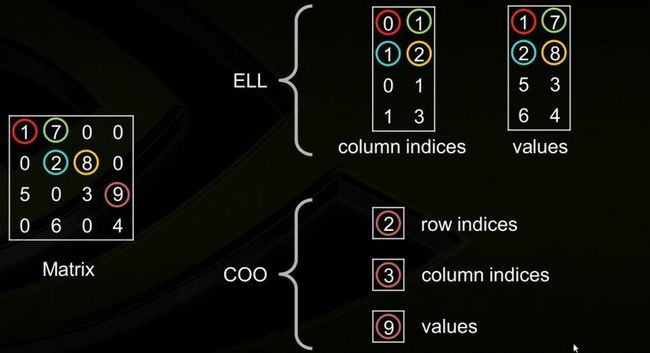
1. Coordinate Format (COO)
这种存储方式的主要优点是灵活、简单。仅存储非零元素以及每个非零元素的坐标。
使用3个数组进行存储:values, rows, andcolumn
参数:矩阵中非零元素的数量 nnz,3个数组的长度均为nnz.
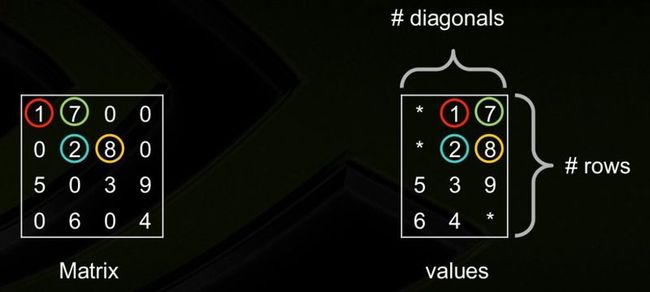
2. Diagonal Storage Format (DIA)
If the sparse matrix has diagonals containing only zero elements, then the diagonal storage format can be used to reduce the amount of information needed to locate the non-zero elements. This storage format is particularly useful in many applications where the matrix arises from a finite element or finite difference discretization.
The Intel MKL diagonal storage format is specified by two arrays:values anddistance, and two parameters:ndiag, which is the number of non-empty diagonals, andlval, which is the declared leading dimension in the calling (sub)programs.
A real or complex two-dimensional array is dimensioned aslval byndiag. Each column of it contains the non-zero elements of certain diagonal ofA. The key point of the storage is that each element invalues retains the row number of the original matrix. To achieve this diagonals in the lower triangular part of the matrix are padded from the top, and those in the upper triangular part are padded from the bottom. Note that the value ofdistance(i) is the number of elements to be padded for diagonali.
An integer array with dimension ndiag. Elementi of the arraydistance is the distance betweeni-diagonal and the main diagonal. The distance is positive if the diagonal is above the main diagonal, and negative if the diagonal is below the main diagonal. The main diagonal has a distance equal to zero.
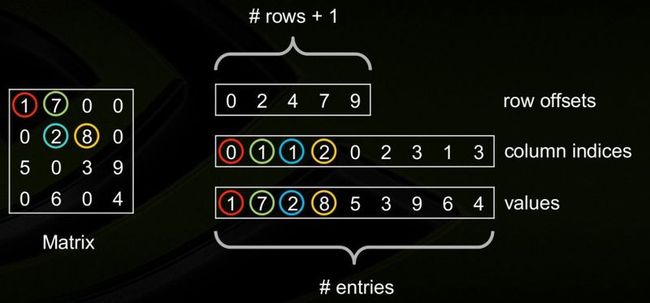
3. Compressed Sparse Row Format (CSR)
The Intel MKL compressed sparse row (CSR) format is specified by four arrays: thevalues,columns,pointerB, andpointerE. The following table describes the arrays in terms of the values, row, and column positions of the non-zero elements in a sparse matrixA.
A real or complex array that contains the non-zero elements ofA. Values of the non-zero elements ofA are mapped into thevalues array using the row-major storage mapping described above.
Element i of the integer array columns is the number of the column inA that contains thei-th value in thevalues array.
Element j of this integer array gives the index of the element in thevalues array that is first non-zero element in a rowj ofA. Note that this index is equal topointerB(j) -pointerB(1)+1.
An integer array that contains row indices, such thatpointerE(j)-pointerB(1)is the index of the element in thevalues array that is last non-zero element in a row j of A.
4. Compressed Sparse Column Format (CSC)
The compressed sparse column format (CSC) is similar to the CSR format, but the columns are used instead the rows. In other words, the CSC format is identical to the CSR format for the transposed matrix. The CSR format is specified by four arrays: values, columns, pointerB, and pointerE. The following table describes the arrays in terms of the values, row, and column positions of the non-zero elements in a sparse matrixA.
A real or complex array that contains the non-zero elements ofA. Values of the non-zero elements ofA are mapped into thevalues array using the column-major storage mapping.
Element i of the integer array rows is the number of the row inA that contains thei-th value in thevalues array.
Element j of this integer array gives the index of the element in thevalues array that is first non-zero element in a columnj ofA. Note that this index is equal topointerB(j) -pointerB(1)+1.
An integer array that contains column indices, such thatpointerE(j)-pointerB(1)is the index of the element in thevalues array that is last non-zero element in a column j ofA.
5. Skyline Storage Format
The skyline storage format is important for the direct sparse solvers, and it is well suited for Cholesky or LU decomposition when no pivoting is required.
The skyline storage format accepted in Intel MKL can store only triangular matrix or triangular part of a matrix. This format is specified by two arrays:values andpointers. The following table describes these arrays:
A scalar array. For a lower triangular matrix it contains the set of elements from each row of the matrix starting from the first non-zero element to and including the diagonal element. For an upper triangular matrix it contains the set of elements from each column of the matrix starting with the first non-zero element down to and including the diagonal element. Encountered zero elements are included in the sets.
An integer array with dimension(m+1), where m is the number of rows for lower triangle (columns for the upper triangle).pointers(i) -pointers(1)+1gives the index of element invalues that is first non-zero element in row (column)i. The value ofpointers(m+1)is set tonnz+pointers(1), wherennz is the number of elements in the arrayvalues.
6. Block Compressed Sparse Row Format (BSR)
The Intel MKL block compressed sparse row (BSR) format for sparse matrices is specified by four arrays:values,columns,pointerB, andpointerE. The following table describes these arrays.
A real array that contains the elements of the non-zero blocks of a sparse matrix. The elements are stored block-by-block in row-major order. A non-zero block is the block that contains at least one non-zero element. All elements of non-zero blocks are stored, even if some of them is equal to zero. Within each non-zero block elements are stored in column-major order in the case of one-based indexing, and in row-major order in the case of the zero-based indexing.
Element i of the integer array columns is the number of the column in the block matrix that contains thei-th non-zero block.
Element j of this integer array gives the index of the element in thecolumns array that is first non-zero block in a rowj of the block matrix.
Element j of this integer array gives the index of the element in thecolumns array that contains the last non-zero block in a rowj of the block matrix plus 1.
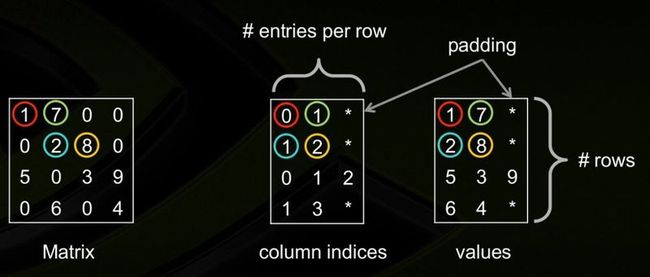
7. ELLPACK (ELL)
8. Hybrid (HYB)
由ELL+COO两种格式结合而成。
选择稀疏矩阵存储格式的一些经验:
1. DIA和ELL格式在进行稀疏矩阵-矢量乘积(sparse matrix-vector products)时效率最高,所以它们是应用迭代法(如共轭梯度法)解稀疏线性系统最快的格式;
2. COO和CSR格式比起DIA和ELL来,更加灵活,易于操作;
3. ELL的优点是快速,而COO优点是灵活,二者结合后的HYB格式是一种不错的稀疏矩阵表示格式;
4. 根据Nathan Bell的工作,CSR格式在存储稀疏矩阵时非零元素平均使用的字节数(Bytes per Nonzero Entry)最为稳定(float类型约为8.5,double类型约为12.5),而DIA格式存储数据的非零元素平均使用的字节数与矩阵类型有较大关 系,适合于StructuredMesh结构的稀疏矩阵(float类型约为4.05,double类型约为8.10),对于Unstructured Mesh以及Random Matrix,DIA格式使用的字节数是CSR格式的十几倍;
5. 从我使用过的一些线性代数计算库来说,COO格式常用于从文件中进行稀疏矩阵的读写,如matrix market即采用COO格式,而CSR格式常用于读入数据后进行稀疏矩阵计算。
其他相关链接:
1. Intel MKL 库中使用的稀疏矩阵格式
http://software.intel.com/sites/products/documentation/hpc/mkl/mklman/GUID-9FCEB1C4-670D-4738-81D2-F378013412B0.htm
2. Sparse Matrix Representations & Iterative Solvers, Lesson 1 by Nathan Bell
http://www.bu.edu/pasi/files/2011/01/NathanBell1-10-1000.pdf
欢迎来到我的CSDN博客:http://blog.csdn.net/anshan1984/