简介
杨氏矩阵是在很多面试和讨论中用到比较多的一个话题。它本身独特的构造使得它的一些增删查改的操作和堆排序以及二分搜索的思想很类似。它本身问题不难,实际操作的时候会稍微有点繁琐。
问题
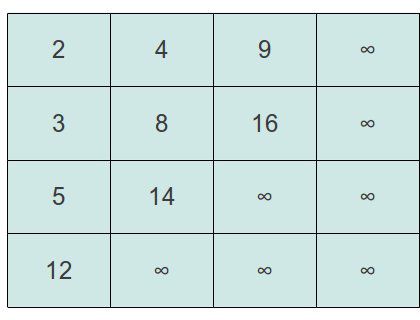
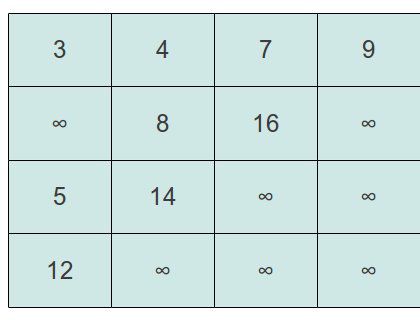
假定我们有一个mxn的矩阵,它的每一行以及每一列都是排好序的。我们可以称这个矩阵为Young tableaus(杨氏矩阵)。在这个矩阵里,可以有某些元素不存在的情况,也就是说,这些位置的值被设置为无穷大(∞)。我们以元素按照非递减的顺序为例,假设我们有这么一组数字{9, 16, 3, 2, 4, 8, 5, 14, 12},我们可以构造一个如下的杨氏矩阵:
由前面的基本定义,我们发现几个很直观的特性:
一、对于每个元素,如果不是值为∞的,它的右边和下面的元素都大于或者等于它。那么,对于整个矩阵来说,它最小的元素肯定在最左上角,也就是元素a[0][0]。
二、由于整个矩阵可以有空缺的元素,我们用∞来表示。那么,如果它最右下角的元素a[m][n]不是∞的话,我们可以推断这个矩阵是满的矩阵,也就是说不存在∞的元素。
ok,有了前面的这部分定义,我们来看看矩阵的几个常见操作吧。
增(insert)
insert元素的过程就是我要新增加一个元素到矩阵中,保证我插入的这个元素最后要放在一个适当的位置以满足杨氏矩阵的特性。这里最关键的就是有两个点:1. 找到一个初始插入的点。 2. 调整,将元素放到合适的位置上。
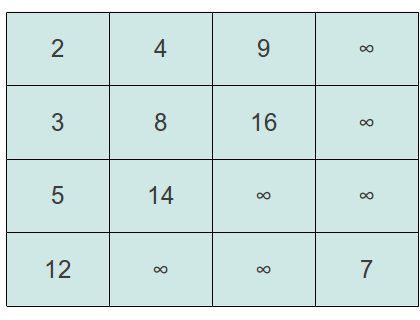
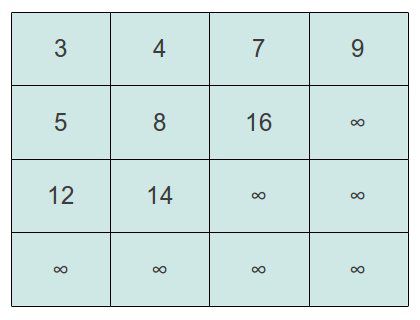
放元素的话,我们可以考虑到,只要这个矩阵不是满的,那么他最后的那个放置元素的点应该是最右下角的那个。我们可以考虑先把元素放到这个点。然后再来调整。以前面给出的矩阵为例,假设我们要插入一个元素7,我们插入元素后的矩阵结果如下:
调整的话,我们考虑,假设它左边的元素和上面的元素都存在,而且比自己大的话,我们就需要取中间最大的那个元素,和当前元素交换位置。对于两边元素一样大的情况,先比较同行的或者同列的都可以。假定我们先比较同一列的,然后比较同一行的,则位置调整的步骤如下:
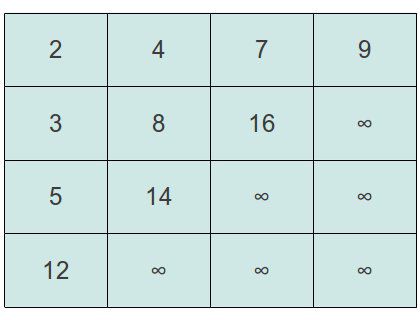
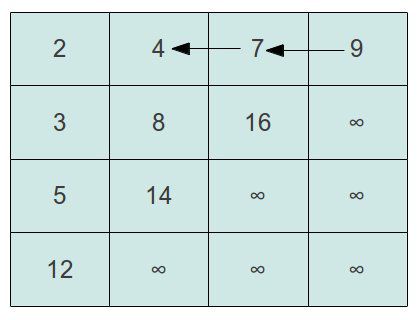
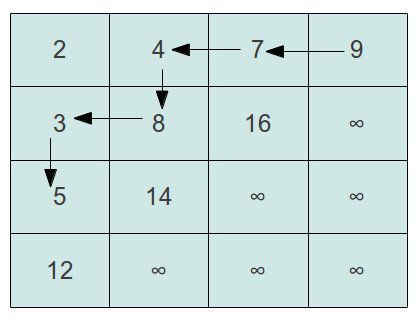
1. 7 和上面的∞比较,因为7小于∞,根据先和同列元素比较的方式,则先将7与它上面的元素交换。这样一直将7交换到了最右上角。如下图:
2. 现在,我们再来比较。7已经到了最右上角,它往上没有元素了,往左有一个9。所以在往左或者往上的方向上比它大的最大元素为9。它需要和9交换。如下图:
前面不断比较交换的过程终止条件是要么元素已经遍历到了矩阵的边角了,要么就是它所有左边和上面的元素都比它要小了。我们可以得出如下的代码:
public static void insert(int[][] a, int k) throws Exception
{
int i = a.length - 1;
int j = a[0].length - 1;
decreaseKeyRec(a, i, j, k);
}
public static void decreaseKeyRec(int[][] a, int i, int j, int k) throws Exception
{
if(a[i][j] < k)
throw new Exception("Invalid key");
a[i][j] = k;
int largesti = i;
int largestj = j;
if(i - 1 >= 0 && a[i - 1][j] > a[i][j])
{
largesti = i - 1;
largestj = j;
}
if(j - 1 >= 0 && a[i][j - 1] > a[largesti][largestj])
{
largesti = i;
largestj = j - 1;
}
if(i != largesti || j != largestj)
{
swap(a, i, j, largesti, largestj);
decreaseKeyRec(a, largesti, largestj, k);
}
}
这里代码实现的一个要点就是比较a[i][j]和a[i-1][j]以及a[i][j-1],找到他们中间最大的那个,然后再将a[i][j]和最大的元素交换。前面decreaseKeyRec()方法用了递归的方式实现。我们也可以写出一个非递归的方法:
public static void decreaseKey(int[][] a, int i, int j, int k) throws Exception
{
if(a[i][j] <= k)
throw new Exception("Invalid key");
a[i][j] = k;
int largesti = i;
int largestj = j;
while(true)
{
if(i - 1 >= 0 && a[i - 1][j] > a[i][j])
{
largesti = i -1;
largestj = j;
}
if(j - 1 >= 0 && a[i][j - 1] > a[largesti][largestj])
{
largesti = i;
largestj = j - 1;
}
if(largesti == i && largestj == j)
break;
swap(a, i, j, largesti, largestj);
i = largesti;
j = largestj;
}
}
这个方法的时间复杂度为O(m+n)。我们在实现中还要考虑的一个点就是,既然我们用∞来表示空缺的元素,在实际实现中该用什么值呢?很多版本的实现用一个特殊的数值。这里假定所有值都在int范围,用Integer.MAX_VALUE来表示这个∞的特殊值。
删(delete)
删除一个元素的过程也可以类似的考虑如下。假定我们要把矩阵中指定的一个元素去掉,那么,我们就需要将它右边或者下面的元素进行调整,来填补原来的位置以保证后续的矩阵符合杨氏矩阵的特性。那么这里就有这么一种思路:
1. 将要删除的元素设置为∞。
2. 再通过将∞的这个元素向友和向下调整,最终移到矩阵满足条件为止。
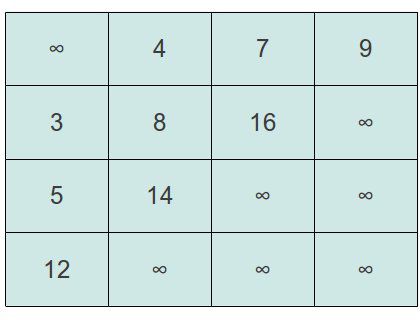
以下图为例,假设我们删除a[0][0]这个点的元素。
在将a[0][0]删除后我们要比较它右边和下面的元素,如果哪个小就交换它和这个最小元素的位置。在这个问题中,a[0][1]为4,a[1][0]为3.所以交换a[0][0]和a[1][0]的位置,如下图:
根据前面的推导,先后交换的元素为5, 12.最终得到如下图的结果:
我们调整的过程称为youngify,代码实现如下:
public static void youngify(int[][] a, int i, int j)
{
int minI = i;
int minJ = j;
if(i + 1 < a.length && a[i + 1][j] < a[i][j])
{
minI = i + 1;
minJ = j;
}
if(j + 1 < a[0].length && a[i][j + 1] < a[minI][minJ])
{
minI = i;
minJ = j + 1;
}
if(minI != i || minJ != j)
{
swap(a, i, j, minI, minJ);
youngify(a, minI, minJ);
}
} 要写一个非递归版的也很容易:
public static void youngifyIter(int[][] a, int i, int j)
{
int minI = i;
int minJ = j;
while(true)
{
if(i + 1 < a.length && a[i + 1][j] < a[i][j])
{
minI = i + 1;
minJ = j;
}
if(j + 1 < a[0].length && a[i][j + 1] < a[minI][minJ])
{
minI = i;
minJ = j + 1;
}
if(i == minI && j == minJ)
break;
swap(a, i, j, minI, minJ);
i = minI;
j = minJ;
}
} 如果我们还记得heapsort里面的heapify,会觉得他们的思想简直是太像了。没错,这就相当于一个heapify的过程。我们进行youngify的时间复杂度为O(m+n)。
查(find)
查找元素有几种办法。一个比较直接的办法就是逐行逐列的去查找,找到之后就返回。这种方法的时间复杂度为O(mxn)。
还有一种就是利用了矩阵的一个性质,他的每行每列都是排序的。那么我们可以用二分查找的办法来做。这样查找的话就需要逐行的去查,时间复杂度大致为O(mlogn)。在这里,前面两种办法就不再详细实现了。
我们来考虑第三种方法。我们的矩阵小的元素在左上方向,大的元素在右下方向。如果我们考虑矩阵的左下角或者右上角的话,会发现一个有意思的事情。就是他们的一个方向的元素大于等于自己而另外一个方向的元素小于等于自己。假定我们从右上角开始来查找,目的元素比当前元素大则向下查,比当前元素小则向左查。这样最终可以找到元素或者遍历到元素的对角位置。以下图为例,假设我们要找元素5,则起始点是在元素9,比较发现5小于9,则找9左边的元素。
我们再依次比较下去,5<7,则比较7左边的元素4,5>4,则再比较4下面的元素8,这样依次下去,形成一个如下图的比较过程:
很显然,有了这么一番分析,我们查找的代码也就出来了:
public static boolean find(int[][] a, int k)
{
int j = a[0].length - 1;
int i = 0;
while(i < a.length && j >= 0)
{
if(a[i][j] > k)
j--;
else if(a[i][j] < k)
i++;
else
return true;
}
return false;
}
这里也可以返回找到元素的坐标。为了偷个懒就直接用有没有查到来作为结果了。 我们也可以很明显的看到,find方法的时间复杂度为O(m+n)。
改(modify)
modify的过程基于前面的讨论其实已经很明了了。我们看,如果我们修改的值比当前值大,就相当于一个youngify的过程,进行调整就可以了。如果修改的值比当前的值小,则利用insert里面的decreaseKey方法,向左上角调整。
总而言之,言而总之,这个过程该怎么做,你懂的。
总结
关于杨氏矩阵本身的问题不多,很多都是通过它的一些应用来讨论。比如说一个这样的矩阵里,有正整数和负整数,那么有多少个正整数呢?这一类的问题挺多的,无非是一些常用特性的变体。大家可以私底下去考虑考虑。