问题描述
假定我们要在一个巨大的数组上面实现一个直接寻址的字典。因为这个数组非常的大,而且一开始可能还包含一些垃圾信息,也就是说,这个建立了的数组是没有被初始化的,它里面可能含有的值不是被都设置为0,而是可能为任意值。而且,如果从头到尾的将这个数组初始化一遍开销太大了,这样又不太现实。现在,假设我们要实现这么一个字典,里面每一个保存的对象使用O(1)的空间,保证search, insert和delete这几种操作的时间复杂度为O(1)。
分析
我们先来简单的看一下这几种操作方法面临的问题。我们采用的是直接寻址的映射方式,比如说,我们给定一个整数k值,那么这个值就是字典里一个名值对的key。所以要找到对应的地址,直接访问数组的k下标就可以了。这样,我们的search, insert, delete方法要跳到对应的位置只需要O(1)的时间。既然前面提到过我们不能遍历整个数组去初始化它,那么这个数组里就包含有不确定的值。如果我们search来查找某个值的时候,我们是没办法确定这个值是不是已经在字典里头了的。所以我们需要某种手段来做一个验证,保证我们找到的数据是合法的。这样,问题的核心就是我们怎么找到一种高效的验证方法。
书上当时还给出了一个提示,使用一个额外的数组当作一个stack来使用。stack的长度表示数组里key的个数。这样,在stack里保存的就是有效的元素。
实现细节
那么,具体验证的细节是怎么安排的呢?这里采用的一个方法叫做“验证环”。假设我们有数组T,它就是这个原始的大数组,我们再定义一个数组S,它作为一个栈来保存合法元素的索引。这样,假定数值k是保存到T中的一个key值,那么T[k]就保存一个对应到栈中间该元素对应的索引值j。同时,我们在栈S[j]这个位置设置的值是k。这样,我们就可以发现两个比较有意思的关系:S[T[k]] = k T[S[j]] = j。因为定义的这两个数据结构可以相互验证,这种对应的关系称之为“验证环”。因为现在所有有效的元素都在栈里,而T[k]保存的是对应栈里面的索引,所以对于任意一个合法的k来说,它有一个这样的对应关系:0 <= T[k] <= top[S]。这里的top[S]表示的是栈S中top元素的索引,也就是最顶端的元素索引值。
按照前面的讨论,我们既然是定义一个字典,也需要一个保存值的地方。我们可以再定义一个数组V,它保存值对象。保存的可以是具体的数值也可以是具体的对象。V的长度和S一样,只是S[T[k]]保存的是key值,而V[T[k]]保存的就是对应的value值。
前面对验证环的描述不太容易让人明白,总感觉有点绕。我们来看看具体的对应实现描述:
Initialization
初始化是最简单的一个过程,既然没法初始化数组T,我们只要设置一下栈的顶就可以了。top = -1。这表示整个栈是空的。在栈不为空的情况下,top指向的是栈最顶端的元素。所以,这一步的操作也是一个O(1)时间复杂度的。
Search
search的过程也相对比较简单。假设我们要找对应key为k的元素。如果它在数组里,则它必须满足0 <= t[k] <= top[S]这一点。而且保证S[T[k]] = k。如果满足的话,我们返回V[T[k]]对应的值,否则返回null。经过这一番讨论我们可以得到下面一段简单的代码:
Object search(int k) {
if(T[k] >= 0 && T[k] <= S.size() && S[T[k]] == k) { // 这里用S.size()来表示S有效元素的长度相当于top[S]
return V[T[k]];
}
else
return null;
}
Insert
插入元素牵涉到一系列栈和元素的调整,我们可以先结合具体的图来讨论。
首先,我们插入元素前有如下三个数组:
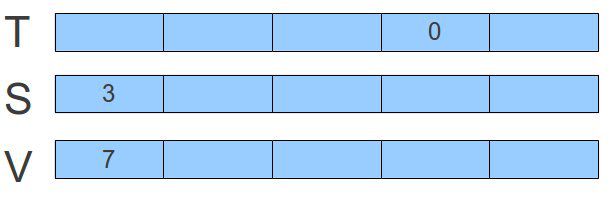
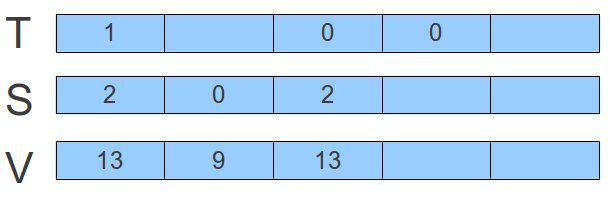
现在,假设我们要在数组T中间插入名值对<3, 7>。按照我们的想法,过程应该如下,1. 首先将key3加入到栈S中。2. 此刻加入的元素肯定是在栈顶,再将栈顶的索引top[s]赋值给T[k]。假定此时栈是空的,则top[S]为0. 3. 再设置V中间对象的值,对应的为V[0] = 7.这样,第一轮插入值之后的结果如下图:
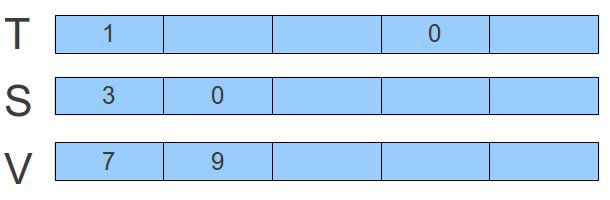
按照前面的思路,如果我们再加入一组数据<0, 9>,则结果如下:
经过这么一番走下来,我们也就可以很容易的写出insert的代码了:
void insert(int k, Object v) {
if(search(k) != null) {
V[T[k]] = v;
}
else {
S.top++; // top为S最顶端元素的index
S[top] = k;
V[top] = v;
T[k] = S.top;
}
}
Delete
delete方法也是一个比较复杂的过程。假定我们要删除某个元素,我们需要首先判断元素是否在字典中。如果该元素在字典中, 这个元素不一定就对应到栈顶,所以我们可以根据k找到栈中间的索引T[k],也可以根据这个T[k]找到对应的值V[T[k]]。找到这个值之后,我们会把这个值删除,一般就是将对应的值置为null。在删除了这个元素之后,我们会发现还有一个问题,这个被删除的元素可能是在栈中间的,这样会形成了一个空洞。既然我们要保证栈里面所有的元素都是有效的,就需要采取一种手段来填补它。一种典型的做法就是取栈顶的元素放到这个空洞里,再将栈长度减一。
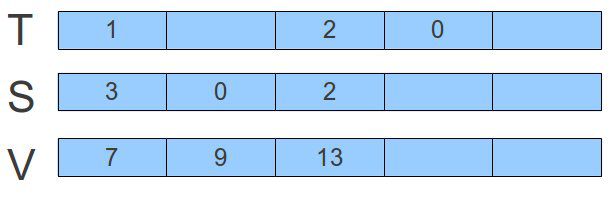
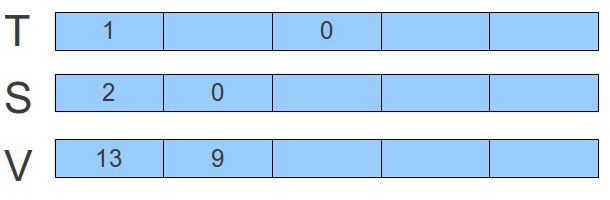
我们再结合图描述一下。假设我们已经有了如下的数据分布:
现在假设我们要删除名值对<3, 7>。我们将做如下的转换:
因为我们的本质上是用栈顶的元素来替换需要被删除的元素,所以对应的步骤如下:
1. 对应k,设置S[T[k]] = S[TOP[S]]
2. 设置对应的value值:V[T[k]] = V[TOP[S]]
3. 因为新的Stack中值已经指向TOP对应的那个元素了,所以有T[S[T[k]]] = T[k]
4. 再将T[k]位置清除,可以设置为T[k] = 0
5. S.top--
这里,我们清除了T[k]的位置,至于V[TOP[S]]则可清也可不清。因为后面如果增加元素就会将它重新置为新的值。
前面的那个图看起来有点模糊,假设我们对应的top元素被移动之后就不显示,则对应的结果如下图:
这样,对应delete的代码如下:
void delete(int k, Object v) {
if(search(k) == null)
return;
else {
S[T[k]] = S[S.top]; // 改变s对应的key
V[T[k]] = V[S.top];
T[S[T[k]]] = T[k]; // s对应的key变了之后,对应的key相应的索引也要更新
T[k] = 0;
S.top--;
}
}
总结
这种验证环的方式粗粗看起来有点绕。刚开始看的时候也是感觉有点扯不清。最好的办法就是画一个图,把他们之间的对应关系描述一下,这样很快就能整理出来了。这里用一个栈来保存有效的元素,同时用另外一个数组来保存对应的值。它能实现一个对元素的快速存取。当然,这也是通过付出额外两个数组的代价得到的。典型的空间换时间思想。