draw2d中的数学公式
图形就必然会存在几何的数学问题:点的旋转,求交点。
1、求点A(a,b)旋转β弧度后B的坐标:
/**
* Returns a new transformed Point of the input Point based on the
* transformation values set.
*/
public Point getTransformed(Point p) {
double x = p.x;
double y = p.y;
double temp;
x *= scaleX;
y *= scaleY;
temp = x * cos - y * sin;
y = x * sin + y * cos;
x = temp;
return new Point(Math.round(x + dx), Math.round(y + dy));
}
a = cosα
b = sinα
x = cos(α + β) = cosα*cosβ - sinα*sinβ
y = sin(α + β) = sinα*cosβ + cosα*sinβ
=>
x = acosβ - bsinβ
y = bcosβ + asinβ
2、计算交点
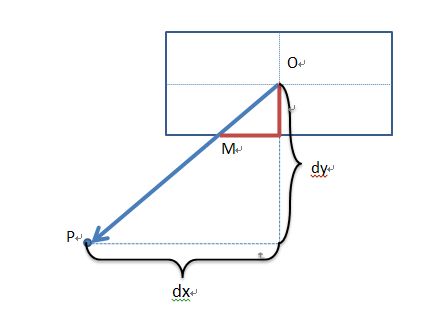
(1)长方形外一点P以及长方形中心O,求PO的连线与长方形的交点:
/**
* Gets a Rectangle from {@link #getBox()} and returns the Point where a
* line from the center of the Rectangle to the Point <i>reference</i>
* intersects the Rectangle.
*/
public Point getLocation(Point reference) {
Rectangle r = Rectangle.SINGLETON;
r.setBounds(getBox());
r.translate(-1, -1);
r.resize(1, 1);
getOwner().translateToAbsolute(r);
float centerX = r.x + 0.5f * r.width;
float centerY = r.y + 0.5f * r.height;
if (r.isEmpty() || (reference.x == (int) centerX && reference.y == (int) centerY))
return new Point((int) centerX, (int) centerY); // This avoids divide-by-zero
float dx = reference.x - centerX;
float dy = reference.y - centerY;
// r.width, r.height, dx, and dy are guaranteed to be non-zero.
float scale = 0.5f / Math.max(Math.abs(dx) / r.width, Math.abs(dy) / r.height);
dx *= scale;
dy *= scale;
centerX += dx;
centerY += dy;
return new Point(Math.round(centerX), Math.round(centerY));
}
1> 判断象限(dx,dy的符号可以确定)
2> 与那条边相交:
float scale = 0.5f / Math.max(Math.abs(dx) / r.width, Math.abs(dy) / r.height);
根据比例算出大边!然后通过相似三角形进行计算。
(2) 椭圆外一点P以及椭圆中心O,求PO的连线与椭圆的交点:
/**
* Returns a point on the ellipse (defined by the owner's bounding box)
* where the connection should be anchored.
*/
public Point getLocation(Point reference) {
Rectangle r = Rectangle.SINGLETON;
r.setBounds(getOwner().getBounds());
r.translate(-1, -1);
r.resize(1, 1);
getOwner().translateToAbsolute(r);
// 相当于
// ref.x = reference.x - r.getCenter().x;
// ref.y = reference.y - r.getCenter().y;
Point ref = r.getCenter().negate().translate(reference);
if (ref.x == 0)
return new Point(reference.x, (ref.y > 0) ? r.bottom() : r.y);
if (ref.y == 0)
return new Point((ref.x > 0) ? r.right() : r.x, reference.y);
float dx = (ref.x > 0) ? 0.5f : -0.5f;
float dy = (ref.y > 0) ? 0.5f : -0.5f;
// ref.x, ref.y, r.width, r.height != 0 => safe to proceed
float k = (float) (ref.y * r.width) / (ref.x * r.height);
k = k * k;
return r.getCenter().translate((int) (r.width * dx / Math.sqrt(1 + k)),
(int) (r.height * dy / Math.sqrt(1 + 1 / k)));
}
1>计算角度θ;
2>通过椭圆的三角坐标代换算出坐标值。