Mathematica分形源码
Mandelbrot分形:
Mandelbrot[zc_] := Module[{z = 0, i =0}, While[i < 100 && Abs[z] < 2, z = z^2 + zc; i++]; i];
DensityPlot[Mandelbrot[xc + I yc], {xc, -2,1}, {yc, -1.5, 1.5}, PlotPoints -> 275,
Mesh -> False, Frame -> False, ColorFunction -> (If[# ≠ 1,
Hue[#], Hue[0, 0, 0]] &)];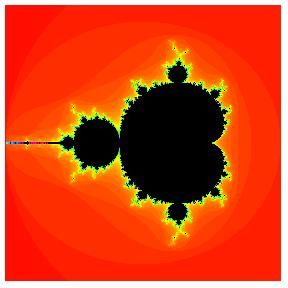
Spirals:
Show[Graphics[RasterArray[Table[r1 = (x - 1)^2 + y^2; r2 = (x +
1)^2 + y^2; Hue[(Sign[y]ArcCos[(x^2 + y^2 -
1)/Sqrt[r1 r2]] - Log[r1/r2])/(2Pi)], {x, -2, 2, 4/
274}, {y, -2, 2, 4/274}]], AspectRatio -> 1]];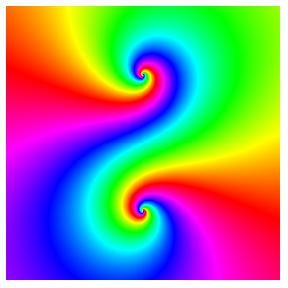
DLA:
n = 100; ix = iy = n/2; i = 0; SeedRandom[0]; image = Table[0, {n}, {n}];
Do[{ix, iy} = Floor[n(0.5 + 0.1{Cos[theta], Sin[theta]})] + 1; image[[ix,
iy]] = 1, {theta, 0, 2 Pi, Pi/180}];
While[(ix - n/2)^2 + (iy - n/2)^2 < (n/2)^2, theta = 2 Pi Random[]; {ix, iy} =
Floor[n(1 + {Cos[theta], Sin[theta]})/2]; drift =
True; While[drift, {ix, iy} = Mod[{ix + Random[Integer, {-1, 1}], iy +
Random[Integer, {-1, 1}]}, n]; drift = Plus @@ Flatten[
image[[Mod[ix + {-1,
0, 1}, n] + 1, Mod[iy + {-1, 0, 1}, n] + 1]]] == 0]; image[[ix + 1,
iy + 1]] = 1 - i/n^1.5; i++];
ListDensityPlot[image, Mesh -> False, Frame -> False];