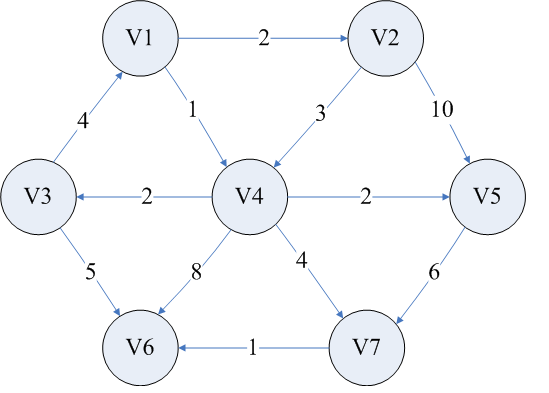
Dijkstra算法分析以及源码
Dijkstra算法 :
时间复杂度O(n*n),空间复杂度O(n*n)。解决单源节点最短路径问题,OSPF动态路由协议应用。
import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
/**
* 贪婪算法
*
*/
public class Dijkstra {
private static final int ENDLESS = Integer.MAX_VALUE/2;
public static int[] dijkstra(int data[][],int vertex){
int result[] = new int[data.length];
for (int i = 1; i < data.length; i++) {
result[i] = data[vertex][i];
}
//初始化S集合
List<Integer> u = new ArrayList<Integer>();
for (int i = 1; i < data.length; i++) {
u.add(i);
}
u.remove(new Integer(vertex));
//初始化U集合
List<Integer> s = new ArrayList<Integer>();
s.add(vertex);
while (!u.isEmpty()) {
int min = ENDLESS;
int minVertex = -1;
//找到U集合中距离【起始点】最近的点,然后将该点从U集合中remove
for (Iterator<Integer> iterator = u.iterator(); iterator.hasNext();) {
Integer integer = (Integer) iterator.next();
if (result[integer] <= min) {
minVertex = integer;
min = result[integer];
}
}
u.remove(new Integer(minVertex));
//更新最短路径
for (Iterator<Integer> iterator = u.iterator(); iterator.hasNext();) {
Integer integer = (Integer) iterator.next();
if (result[minVertex] + data[minVertex][integer] < result[integer]) {
result[integer] = result[minVertex] + data[minVertex][integer];
}
}
}
return result;
}
public static void main(String[] args) {
int data[][] = {
{ENDLESS,ENDLESS,ENDLESS,ENDLESS,ENDLESS,ENDLESS,ENDLESS,ENDLESS},
{ENDLESS,0,2,ENDLESS,1,ENDLESS,ENDLESS,ENDLESS},
{ENDLESS,ENDLESS,0,ENDLESS,3,10,ENDLESS,ENDLESS},
{ENDLESS,4,ENDLESS,0,ENDLESS,ENDLESS,5,ENDLESS},
{ENDLESS,ENDLESS,ENDLESS,2,0,2,8,4},
{ENDLESS,ENDLESS,ENDLESS,ENDLESS,ENDLESS,0,ENDLESS,6},
{ENDLESS,ENDLESS,ENDLESS,ENDLESS,ENDLESS,ENDLESS,0,ENDLESS},
{ENDLESS,ENDLESS,ENDLESS,ENDLESS,ENDLESS,ENDLESS,1,0},
};
int result[] = dijkstra(data, 1);
for (int i = 1; i < result.length; i++) {
System.out.println(result[i]);
}
}
}
运行结果为:
0
2
3
1
3
6
5