1121. Tri Tiling

显然 n 为奇数时，无法拼成。

2*3 有3种排法，设f[n]为方案数，显然可以从前一个状态得到 f[n-2]*3 个排列。

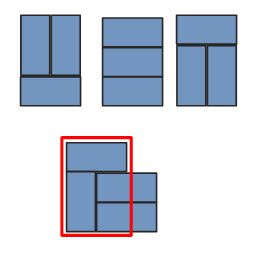
通过观察，比较麻烦的是除了从 f[n-2] 能排出 f[n],另外一种情况是 f[n-2]再加上2格突出（如上图）。此时有2种排法能拼出 f[n]（因为这两格突出可以上下翻转，共两种情况）。

所以我定义了两个数组,re 和unre，分别代表规则的3*n矩形的排列数和不规则（多出2格）矩形的排列数(后者不考虑上下翻转的情况）。

re[2]=3;

unre[2]=1;

re[n]=re[n-2]*3+unre[n-2]*2;

unre[n]=unre[n-2]+re[n-2];

n=0 的时候答案为1。。。。。。。。(╬▔ ω▔)我又wa了。。

#include <stdio.h> const int N=15; int n; int re[N],unre[N]; void pre() { re[0]=3; unre[0]=1; for (int i=1; i<15; ++i) { re[i]=re[i-1]*3+unre[i-1]*2; unre[i]=re[i-1]+unre[i-1]; } } int main(int argc, char *argv[]) { pre(); /* for (int i=0; i<15; ++i) { printf("%d/n", re[i]); }*/ while ( scanf("%d", &n), n!=-1 ) { if ( n==0 ) { printf("1/n"); } else if ( n & 1 ) { printf("0/n"); } else { printf("%d/n", re[ (n>>1) -1 ]); } } return 0; }