世界名画陈列馆问题(回溯法)
一、算法问题描述:
世界名画陈列馆问题。世界名画陈列馆由m×n个排列成矩形阵列的陈列室组成。为了防止名画被盗,需要在陈列室中设置警卫机器人哨位。每个警卫机器人除了监视它所在的陈列室外,还可以监视与它所在的陈列室相邻的上、下、左、右4 个陈列室。试设计一个安排警卫机器人哨位的算法,使得名画陈列馆中每一个陈列室都在警卫机器人的监视之下,且所用的警卫机器人数最少。
二、算法问题形式化表示
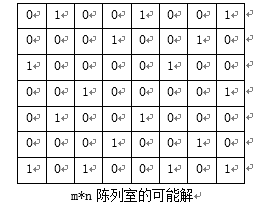
本问题的m*n的陈列室的解可表示如下图所示。其中1代表在该陈列室设置警卫机器人哨位,0表示未在该陈列室设置警卫机器人哨位。
最为极端的情况是所有元素的值为1。那什么情况下是最优解呢?就是设置警卫机器人哨位数最少即为最优。因为每个矩阵中的值都可以为1或0,有m*n个元素,有 种可能满足约束条件的矩阵,要从 种可能中遍历找到满足约束条件的1的个数最小的矩阵。由此可见这是一个NP问题。这里的约束条件就是当某一个元素为1时,相邻的4个方向上的元素值可以为0。
三、期望输入与输出
输入:
第一行有2 个正整数m和n (1≤m,n≤20)
输出:
将计算出的警卫机器人数及其最佳哨位安排输出。第一行是警卫机器人数;接下来的m行中每行n个数,0 表示无哨位,1 表示哨位。
样例输入:
4 4
样例输出:
4
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
四、算法分析与步骤描述
从上到下、从左到右的顺序依次考查每一个陈列室设置警卫机器人哨位的情况,以及该陈列室受到监视的情况,用[i,j]表示陈列室的位置,用x[i][j]表示陈列室[i,j]当前设置警卫机器人哨位的状态。当x[i][j]=1时,表示陈列室[i,j]设置了警卫机器人,当x[i][j]=0时,表示陈列室[i,j]没有设置了警卫机器人。用y[i][j]表示陈列室[i,j]当前受到监视的的警卫机器人的数量。当y[i][j]>0时,表示陈列室[i,j]受到监视的警卫机器人的数量,当y[i][j]=0时,表示陈列室[i,j]没有受到监视。设当前已经设置的警卫机器人的哨位数为k,已经受到监视的陈列室的数量为t,当前最优警卫机器人哨位数为bestc。
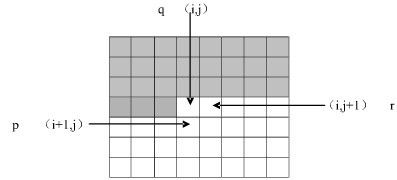
设回溯搜索时,当前关注的陈列室是[i,j],假设该陈列室已经受到监视,即y[i][j]==1,
此时在陈列室[i,j]处设置一个警卫机器人哨位,即x[i][j]==1,相应于解空间树的一个节点q,在陈列室[i+1,j]处设置一个机器人哨位,x[i+1][j]==1,相应于解空间树的另一个节点p。容易看出,以q为根的子树的解,不优于以p为根的子树的解,以q为根的子树可以剪去。因此,在以从上到下,从左到右的顺序依次考察每一个陈列室时,已受监视的陈列室不必设置警卫机器人哨位。
设陈列室[i,j]是从上到下、从左到右搜索到的第一个未受监视的陈列室,为了使陈列室[i,j]受到监视,可在陈列室[i+1,j]、[i,j]、[i,j+1]处设置警卫机器人哨位,在这3处设置哨位的解空间树中的结点分别为p、q、r。
当y[i][j+1]==1时,以q为根的子树的解,不优于以p为根的子树的解,当y[i][j+1]==1且y[i][j+2]==1时,以r为根的子树的解,不优于以p为根的子树的解。搜索时应按照p、q、r的顺序来扩展结点,并检测节点p对节点q和节点r的控制条件。
int [][]bestx=new int[MAX][MAX]; //x用来设置当前警卫,y用来表示监控//情况,bestx返回最终结果
int n, m, best, k = 0, t = 0; //当前已设置的警卫数为k,受监视的陈列室//数为t,当前最少警卫数为best
void change(int i, int j) { //在(i, j)处设置一个警卫,并改变其周围受//监控情况
x[i][j] = 1;
k++;
for (int r = 1; r <= 5; r++) { //在自己本身跟上下左右五个地方设置受控
int p = i + d[r][1];
int q = j + d[r][2];
y[p][q]++;
if (y[p][q] == 1)
t++;
}
}
void restore(int i, int j){} //撤销在(i, j)处设置的警卫,并改变其周围//受监控情况
void search(int i, int j){} //回溯搜索, 从上到下、从左至右搜索没被监控的//位置
五、问题实例及算法运算步骤
首先先说一下监控安置的策略,本思想是安置监控的数量由少到多的策略。
然后用一维数组来记录监控的安装位置
4*4矩阵相应的一维数组就是array[16]一共16个空间,转换成矩阵坐标也比较简单如在array数组中坐标array[8]则对应的矩阵坐标是Matrix[8%4][8/4]所以完全可以用一维数组来替代矩阵;
再根据一维数组来计算所有安置的可能情况如2*3矩阵共6个空间,假如我要在6个空间安置3个监控则相当于离散数学中组合的概念即C(6,3) = 20;
设陈列馆由m*n个陈列室组成,因为不存在重复监视,所以很多情况下都无解,我们采用的做法是根据m和n的值进行分类讨论。首先,先比较m、n大小,使m始终大于n,方面程序书写。分三种情况讨论:
n=1 这时可以直接写出最优解:
当m mod 3=1时,将哨位置于(1,3k+1);
当m mod 3=0或2时,将哨位置于(2,3k+2),其中k=0、1、…、m/3。
n=2 这种情形下必须2端分别设置2个哨位,他们各监视三个陈列室。那么当m为偶数时问题就无解了。
当m为奇数时,将哨位分别至于(1,4k+3)和(2,4k+1),k=0、1、…、m/4。
n>2 容易验证
当n=3,m=3和n=3,m=4时无解,n=4,m=4有解。
设置哨位时,允许在的n+1行和m+1列设置哨位,但不要求的第n+1行和m+1列陈列室受到监视,那么当n>=3且m>=5时在不重复监视下有解那么n=3,m=5的不可重复监视问题一定有解。但是通过验证n=3,m=5的不可重复监视哨位设置问题无解,那么当n>=3且m>=5时在不重复监视下无解。
通过以上讨论就将所有情况分析完全了,简单写一个包含多个条件判断的程序就可以实现该算法。
六、算法运行截图
七、算法复杂度分析
回溯法需要为问题定义一个解空间,这个解空间必须至少包含问题的一个解(可能是最优的)。使用递归回溯法解决问题的优点在于它算法思想简单,而且它能完全便利搜索空间,肯定能找到问题的最优解;但是由于此问题解的总组合数有 个,因此,随着物件数n的增大,其解的空间将以 级增长,因此时间复杂度为:O(n )。
下面是完整代码:
import java.util.Scanner;
public class Test5 {
static final int MAX = 1000;
static int d[][] = { {0,0,0}, {0,0,0}, {0,0,-1}, {0,-1,0}, {0,0,1}, {0,1,0} };
static int [][]x=new int[MAX][MAX];
static int [][]y=new int[MAX][MAX];
static int [][]bestx=new int[MAX][MAX]; //x用来设置当前警卫,y用来表示监控情况,bestx返回最终结果
static int n, m, best, k = 0, t = 0; //当前已设置的警卫数为k,受监视的陈列室数为t,当前最少警卫数为best
static int t1, t2, more; //判断下界剪枝的条件参数
boolean p;
/**
* 世界名画陈列馆问题(回溯法)
*/
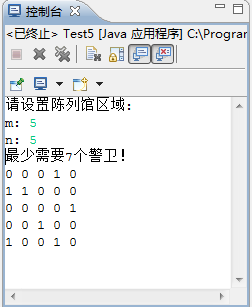
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println("请设置陈列馆区域:");
System.out.print("m: ");
Scanner sc1=new Scanner(System.in);
m=Integer.parseInt(sc1.next());
System.out.print("n: ");
sc1=new Scanner(System.in);
n=Integer.parseInt(sc1.next());
compute(); //计算
System.out.println("最少需要"+best+"个警卫!");
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++)
System.out.print( bestx[i][j]+" ");
System.out.println();
}
}
static void change(int i, int j) { //在(i, j)处设置一个警卫,并改变其周围受监控情况
x[i][j] = 1;
k++;
for (int r = 1; r <= 5; r++) { //在自己本身跟上下左右五个地方设置受控
int p = i + d[r][1];
int q = j + d[r][2];
y[p][q]++;
if (y[p][q] == 1)
t++;
}
}
static void restore(int i, int j) { //撤销在(i, j)处设置的警卫,并改变其周围受监控情况
x[i][j] = 0;
k--;
for (int r = 1; r <= 5; r++) {
int p = i + d[r][1];
int q = j + d[r][2];
y[p][q]--;
if (y[p][q] == 0)
t--;
}
}
static void search(int i, int j) { //回溯搜索
do { //从上到下,从左至右搜索没被监控的位置
j++;
if (j > m) {
i++;
j = 1;
}
} while (!((y[i][j] == 0) || (i > n)));
if (i > n) {
if (k < best) { //刷新警卫值
best = k;
for (int p = 1; p <= n; p++)
for (int q = 1; q <= m; q++)
bestx[p][q] = x[p][q];
return;
}
}
if (k + (t1 - t)/5 >= best) return; //警卫数下界 = 还需设置的最少警卫数 + 现有的警卫数
if ((i < n - 1) && (k + (t2 - t)/5 >= best)) return; //如果比最优警卫数多的话,就剪去这一分枝
if (i < n) { //结点p
change(i + 1, j);
search(i, j); //递归搜索下一个点
restore(i + 1,j); //恢复
}
if (y[i][j + 1] == 0) { //结点q
change(i, j);
search(i, j);
restore(i, j);
}
if ((j < m) && ((y[i][j + 1] == 0) || (y[i][j + 2] == 0))) { //结点r
change(i, j + 1);
search(i, j);
restore(i, j + 1);
}
}
static void compute() {
more = m/4 + 1;
if (m % 4 == 3)
more++;
else if (m % 4 == 2)
more += 2;
t2 = m * n + more + 4;
t1 = m * n + 4;
best = 65536;
if (m == 1 && n == 1) {
System.out.println(1);
System.out.println(1);
}
for (int i = 0; i <= m + 1; i++) { //在整个外面加上一圈,便于处理边界情况
y[0][i] = 1;
y[n + 1][i] = 1;
}
for (int i = 0; i <= n + 1; i++) {
y[i][0] = 1;
y[i][m + 1] = 1;
}
search(1, 0);
}
}