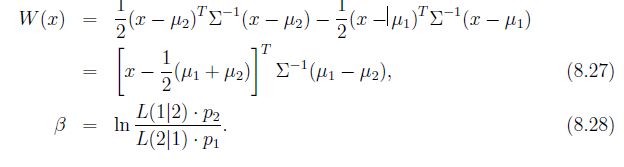R语言 分类算法

一、线性分类法

通俗点理解线性分类法就是画条线，尽量的使同样类别的点，落在线的同一边。如果是三维的，那么画一个面。当不同类样本的协方差矩阵相同时，我们可以在R中使用MASS包的lda函数实现线性判别。lda函数以Bayes判别思想为基础。当分类只有 两种且总体服从多元正态分布条件下，Bayes判别与Fisher判别、距离判别是等价的。
本例使用iris数据集来对花的品种进行分类。首先载入 MASS包，建立判别模型，其中的prior参数表示先验概率。然后利用table函数建立混淆矩阵，比对真实类别和预测类别。
当样本的协方差矩阵相同时用lda函数判别

#用线性判别法，来对鸢尾花数据集进行判别。
> library(MASS)
> model <- lda(Species ~ ., data=iris,prior=c(1,1,1)/3) #prior是先验概率。
> predict(model,iris)$class  #利用模型预测
  [1] setosa     setosa     setosa     setosa     setosa     setosa     setosa    
  [8] setosa     setosa     setosa     setosa     setosa     setosa     setosa    
 [15] setosa     setosa     setosa     setosa     setosa     setosa     setosa    
 [22] setosa     setosa     setosa     setosa     setosa     setosa     setosa    
 [29] setosa     setosa     setosa     setosa     setosa     setosa     setosa    
 [36] setosa     setosa     setosa     setosa     setosa     setosa     setosa    
 [43] setosa     setosa     setosa     setosa     setosa     setosa     setosa    
 [50] setosa     versicolor versicolor versicolor versicolor versicolor versicolor
 [57] versicolor versicolor versicolor versicolor versicolor versicolor versicolor
 [64] versicolor versicolor versicolor versicolor versicolor versicolor versicolor
 [71] virginica  versicolor versicolor versicolor versicolor versicolor versicolor
 [78] versicolor versicolor versicolor versicolor versicolor versicolor virginica 
 [85] versicolor versicolor versicolor versicolor versicolor versicolor versicolor
 [92] versicolor versicolor versicolor versicolor versicolor versicolor versicolor
 [99] versicolor versicolor virginica  virginica  virginica  virginica  virginica 
[106] virginica  virginica  virginica  virginica  virginica  virginica  virginica 
[113] virginica  virginica  virginica  virginica  virginica  virginica  virginica 
[120] virginica  virginica  virginica  virginica  virginica  virginica  virginica 
[127] virginica  virginica  virginica  virginica  virginica  virginica  virginica 
[134] versicolor virginica  virginica  virginica  virginica  virginica  virginica 
[141] virginica  virginica  virginica  virginica  virginica  virginica  virginica 
[148] virginica  virginica  virginica 
Levels: setosa versicolor virginica

当样本的协方差矩阵不同时，使用qda()函数判别

>model2=qda(Species~.,data=iris,cv=T) #cv使用留一交叉检验（leave-one-out cross-validation），并自动生成预测值
>predict(model)$posterior  #查看后验概率

使用这两种线性判别法，需要总体服从多元正态分布。

二、距离判别法

算距离，某个样本点离哪个类比较近，就判断为哪个类别。但这里计算的不是欧氏距离，而是马氏距离。

distinguish.distance <- function(TrnX, TrnG, TstX = NULL, var.equal = FALSE){
  if(is.factor(TrnG) == FALSE){         #如果传入的trnG 不是因子，就当成第二个类别看待
    mx <- nrow(TrnX); mg <- nrow(TrnG)  #把他们放到一起，总共两个分类
    TrnX <- rbind(TrnX, TrnG)
    TrnG <- factor(rep(1:2, c(mx, mg)))
  }
  if(is.null(TstX)){
    TstX <- TrnX
  }
  if(is.vector(TstX)){                 #如果传入的测试集是向量，变成矩阵并且竖起来
    TstX <- t(as.matrix(TstX))
  }else if(is.matrix(TstX) != TRUE){   #不是矩阵的变成矩阵
    TstX <- as.matrix(TstX)
  }
  if(is.matrix(TrnX) != TRUE){         #把训练集当矩阵对待
    TrnX <- as.matrix(TrnX)
  }
  nx <- nrow(TstX)                             #测试集总共有行
#生成一个只有一行的矩阵，长度为要预测的数据的个数，这个用来存测试集的分类
  blong <- matrix(rep(0, nx), nrow=1, dimnames=list("blong", 1:nx))
  g <- length(levels(TrnG)) #有多少分类
  mu <- matrix(0, nrow=g, ncol=ncol(TrnX)) #生成列方向上的平均值矩阵，行数为类别数量
  for (i in 1:g){
    mu[i,] <- colMeans(TrnX[TrnG==i,])   #求每一列数据，每一个水平的平均值
  }
  D <- matrix(0, nrow=g, ncol=nx)        #新建一个矩阵用来存 待测样本点到个类别的距离。行数是类别数，
  if(var.equal == TRUE || var.equal == T){
    for(i in 1:g)｛
      D[i,] <- mahalanobis(TstX, mu[i,], var(TrnX))
    ｝
  }else{
    for (i in 1:g)｛
      D[i,] <- mahalanobis(TstX, mu[i,], var(TrnX[TrnG==i,]))
    ｝
  }
  for (j in 1:nx){
    dmin <- Inf
    for (i in 1:g)
      if (D[i,j] < dmin){                 #循环着跑一下，比较各个类别见哪个距离是最短的。就属于哪个类别
        dmin <- D[i,j]; blong[j] <- i
      }
    }
  blong #输出
}
#上面程序中mahalanobis（向量或矩阵，样本中心，协方差矩阵）是用来求马氏距离的。

> source("E:hutao\\learning\\rscript\\myR.R")
> x <- iris[,1:4]
> g <- gl(3,50)
> distinguish.distance(x,g)
      1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
blong 1 1 1 1 1 1 1 1 1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1
      31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57
blong  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  2  2  2  2  2  2  2
      58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84
blong  2  2  2  2  2  2  2  2  2  2  2  2  2  3  2  3  2  2  2  2  2  2  2  2  2  2  3
      85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108
blong  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2   2   3   3   3   3   3   3   3   3
      109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128
blong   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3
      129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148
blong   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3
      149 150
blong   3   3

三、贝叶斯分类器

前提假设，总体是正态分布的。
记 统计量ECM(R1, R2) = L(2|1)P(2|1)p1 + L(1|2)P(1|2)p2， 前面是明明是1类，却被判定为2类的概率乘以损失L(2|1)
，后面是另一种损失。 我们要划定分类，使得这个ECM最小。数学上可以证明，在上面这个值达到最小的情况下划分出来的R1、R2，f1(x)/f2(x) 和 L(1|2)p2/L(2|1)p1的大小关系是这2个类的分界。前者大于后者的时候是R1类，另一种情况是R2类。其中f1(x)是R1类的概率密度函数。p是先验概率，L是损失。对上面两个值同时取对数，然后进行约简，得到左边的w 和右边的 β。在两个类别总体协方差相同和不同的情况下，分别求的下面的值

现在变成了 W（x）>=β是 R1类，另一个是R2类。神奇的事情发生了，w统计量和我们在距离判别法里算的距离的差值是一样的。所以贝叶斯可以看成是距离判别法的推广。当β值 = 0 的时候，贝叶斯就是距离判别。
上面是只有两种类型的情况。如果有多种类型，我们先假设，误判的损失是相同的。然后计算d统计量 ，即
dj(x) =(1/2)(x − μj)T Σ^(−1) (x − μj) − ln pj (协方差不同时还要− (1/2)ln(|Σj |)), 计算每个样本到各个分类的d统计量，谁最小就把样本判到谁的类里。根据这个办法写R函数

distinguish.bayes <- function(TrnX, TrnG, p = rep(1, length(levels(TrnG))),
  TstX = NULL, var.equal = FALSE){         #p是先验概率，默认都是1
  if(is.factor(TrnG) == FALSE){
    mx <- nrow(TrnX); mg <- nrow(TrnG)
    TrnX <- rbind(TrnX, TrnG)
    TrnG <- factor(rep(1:2, c(mx, mg)))
  }                        #上面的代码还是老意思，如果分别传入两个类别的数据，就合成一个。并给因子
  if(is.null(TstX) == TRUE){
    TstX <- TrnX         #没给测试集，就用训练集代替
  }
  if(is.vector(TstX) == TRUE){
    TstX <- t(as.matrix(TstX))   #变成竖着的一维矩阵
  }else if(is.matrix(TstX) != TRUE){
    TstX <- as.matrix(TstX)      #给了测试集 就变成矩阵
  }
  if(is.matrix(TrnX) != TRUE){
    TrnX <- as.matrix(TrnX)    #变成矩阵
  }
  nx <- nrow(TstX)      #测试集样本数
  blong <- matrix(rep(0, nx), nrow=1,  
  dimnames=list("blong", 1:nx))
  g <- length(levels(TrnG))
  mu <- matrix(0, nrow=g, ncol=ncol(TrnX))
  for(i in 1:g){
    mu[i,] <- colMeans(TrnX[TrnG==i,])
  }
  D <- matrix(0, nrow=g, ncol=nx)
  if(var.equal == TRUE || var.equal == T){
    for(i in 1:g){
      d2 <- mahalanobis(TstX, mu[i,], var(TrnX))
      D[i,] <- d2 - 2*log(p[i])
    }
  }else{
    for(i in 1:g){
      S <- var(TrnX[TrnG==i,])
      d2 <- mahalanobis(TstX, mu[i,], S)
      D[i,] <- d2 - 2*log(p[i])-log(det(S))
    }
  }
  for(j in 1:nx){
    dmin <- Inf
    for(i in 1:g){
      if(D[i,j] < dmin){
        dmin <- D[i,j]
        blong[j] <- i
      }
    }
  }
  blong
} #跟上面的距离判别法比较雷同

> source("E:\\hutao\\learning\\rscript\\myR.R")
> distinguish.bayes(iris[1:4],gl(3,50))
      1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
blong 1 1 1 1 1 1 1 1 1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1
      28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
blong  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  2
      52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
blong  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  3  2  3  2  3  2  2
      76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
blong  2  2  3  2  2  2  2  2  3  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2
      100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117
blong   2   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3
      118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135
blong   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3
      136 137 138 139 140 141 142 143 144 145 146 147 148 149 150
blong   3   3   3   3   3   3   3   3   3   3   3   3   3   3   3

四、Fisher判别

discriminiant.fisher <- function(TrnX1, TrnX2, TstX = NULL){
  if(is.null(TstX) == TRUE){
    TstX <- rbind(TrnX1,TrnX2)
  }
  if(is.vector(TstX) == TRUE){
    TstX <- t(as.matrix(TstX))
  }else if(is.matrix(TstX) != TRUE){
    TstX <- as.matrix(TstX)
  }
  if(is.matrix(TrnX1) != TRUE){
    TrnX1 <- as.matrix(TrnX1)
  }
  if(is.matrix(TrnX2) != TRUE){
    TrnX2 <- as.matrix(TrnX2)
  }
  nx <- nrow(TstX)
  blong <- matrix(rep(0, nx), nrow=1, byrow=TRUE,
  dimnames=list("blong", 1:nx))
  n1 <- nrow(TrnX1); n2 <- nrow(TrnX2)
  mu1 <- colMeans(TrnX1); mu2 <- colMeans(TrnX2)
  S <- (n1-1)*var(TrnX1) + (n2-1)*var(TrnX2)
  mu <- n1/(n1+n2)*mu1 + n2/(n1+n2)*mu2
  w <- (TstX-rep(1,nx) %o% mu) %*% solve(S, mu2-mu1);
  for (i in 1:nx){
    if(w[i] <= 0){
      blong[i] <- 1
    }else{
      blong[i] <- 2
    }
  }
  blong
}

五、决策树

http://www.statmethods.net/advstats/cart.html
照着敲一把

> library(rpart)
> fit <- rpart(Kyphosis ~ Age + Number + Start, method="class", data=kyphosis)
> fit
> plot(fit,uniform=T,main="myTree")
> text(fit,use.n=T,all=T,cex=0.8)