几何之美(二)
在Processing中,最常用也是最常见的当属点,线,圆等的坐标了,那么先从坐标讲起。目前使用最广泛的度量体系就属笛卡尔坐标系统了。笛卡尔数学由著名的法国哲学家、物理学家、生理学家、数学家勒奈·笛卡尔(1596-1650)发明,并以他的名字命名。笛卡尔不仅创立了解析几何,将当时完全分离的代数学和几何学联系到了一起,还在回答“怎样判断某件事物是真的?”这个哲学问题上迈出了一大步。
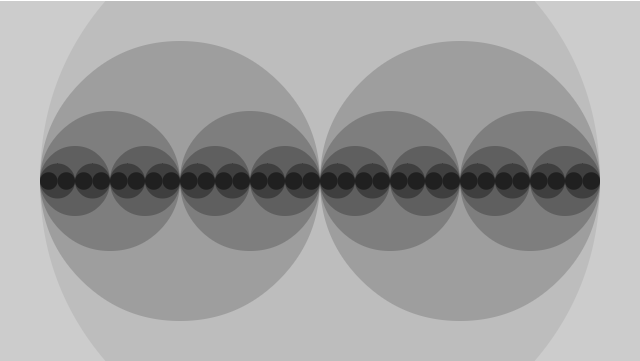
大家看下图:
void setup() {
size(640, 360);
noStroke();
noLoop();
}
void draw() {
drawCircle(width/2, 280, 6);
}
void drawCircle(int x, int radius, int level) {
float tt = 126 * level/4.0;
fill(tt);
ellipse(x, height/2, radius*2, radius*2);
if(level > 1) {
level = level - 1;
drawCircle(x - radius/2, radius/2, level);
drawCircle(x + radius/2, radius/2, level);
}
}
通过了简短的代码,绘制了很多对称呈灰度显示的大圆和小圆。通过在draw()方法中调用drawCircle()这个画圆的工具,我们轻松地生产出他们。不知道大家有没有发现,我可以将两个同级对称的圆用坐标轴进行分割,那么两个圆就是相对于y轴镜面对称,每两个同级圆其实就是共享一个坐标系统。那么其实我这里就是绘制了31个嵌套的坐标系统(除最外面的大圆)。
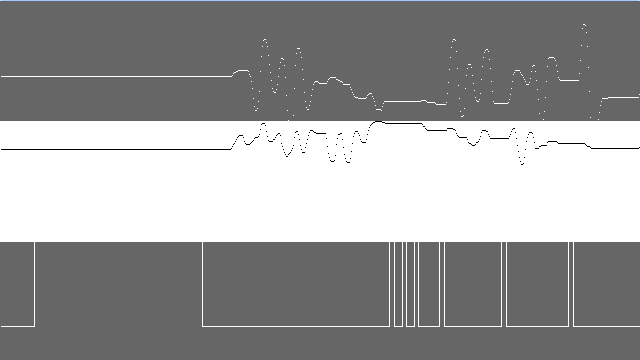
再如下图:
一上来大家可能看的不是太明白。这是什么呀?可能有些人会发问。其实这是三张频谱图。用来分别映射我们鼠标的动作:最上面那张是表示鼠标在x轴上的运动情况,中间那幅表示鼠标在y轴上的运动情况,而最下面那张表示鼠标点击这个动作的发生和延迟情况。
下面是他的代码实现:
int[] xvals;
int[] yvals;
int[] bvals;
void setup()
{
size(640, 360);
noSmooth();
xvals = new int[width];
yvals = new int[width];
bvals = new int[width];
}
int arrayindex = 0;
void draw()
{
background(102);
for(int i = 1; i < width; i++) {
xvals[i-1] = xvals[i];
yvals[i-1] = yvals[i];
bvals[i-1] = bvals[i];
}
// Add the new values to the end of the array
xvals[width-1] = mouseX;
yvals[width-1] = mouseY;
if(mousePressed) {
bvals[width-1] = 0;
} else {
bvals[width-1] = 255;
}
fill(255);
noStroke();
rect(0, height/3, width, height/3+1);
for(int i=1; i<width; i++) {
stroke(255);
point(i, xvals[i]/3);
stroke(0);
point(i, height/3+yvals[i]/3);
stroke(255);
line(i, 2*height/3+bvals[i]/3, i, (2*height/3+bvals[i-1]/3));
}
}
不知道大家有没有发现,前面两张图很像我们中学时代学的正弦与余弦曲线。上面的白色平行线和中间那条黑色平行线就是他们分别对应的x轴,神奇吧。如果你鼠标移动的越快,这些曲线的幅宽则越小。同样道理,如果你停留在鼠标上的时间越长,那么当你点击之后移开鼠标之前产生的直方图的跨度则越大。
这些都是几何学中坐标轴的妙用,通过坐标轴的变换我们还可以得出很多很多有趣的2D和3D图形。大家还不赶快开动脑筋和双手来创造他们吧。
这一节就先讲到这里,欢迎关注本连载博文《几何之美》的下一篇。谢谢大家!