北大ACM暑期培训课程目录
本文出自:http://blog.csdn.net/svitter
目录:
北大ACM暑期培训课程目录(二)(搜索)
北大ACM暑期培训课程目录(三)(图论)
北大ACM暑期培训课程目录(四)(计算几何)
北大ACM暑期培训课程目录(五)(网络流)
今天ACM暑期实训开始了,今天讲述的内容是:(点击下载课程资源)
7.18 依然是动态规划
7.17 动态规划
7.16 数学题:组合数学,数论等
7.15 数据结构(二): 并查集, DFA, Trie图等
7.14 数据结构(一): 线段树,树状数组,二维线段树。
一.线段树,树状数组,二维线段树:
1.线段树:invertal tree (称为区间树更加合适)
作用:快速区间查询,用于解决区间统计的有关问题。
重点:同层节点不重叠。
每层最多有两个终止节点。
更新和进行区间分解的时间复杂度均为log(n);
方法:调用会多次使用递归更新插入查询;
空间:开空间的时候,一般情况下开4n大小,2*2log[n] - 1 <= 4n;
关键在于是否接近2的幂。如果不超过2的幂一般开3n即可,超过开4n
不同的情况可能MLE,
具体的资料可以网上查询。
参考题目:
POJ3264——Balanced Lineup(线段树)
POJ3468__A Simple Problem with Integers (线段树)
hdu1754___I Hate It (线段树)
2.树状数组:
作用:与线段树相同,快速求出任意区间的和。但是相对于线段树,更加容易编写,速度也有优势。
单个元素修改,反复求区间。
参考题目:树状数组_POJ树状数组初探
3.二维线段树,二维树状数组:
二维二叉树是一棵4叉树。也可以用树套树实现,两层线段树。
整个线段树使用二维数组实现。
用完全二叉树,一般情况下3倍即可。
二维即对应之前的数字找对应的数组编号(省略了l,r)
更新时只需要对相应的行列更新即可。
二.并查集,DFA,Trie树
1.并查集
1.改进1:
较小的rank挂在较大的rank根部,这样新生成的树的深度也不会超过原来较大的rank(树的深度)。平衡就是log量级的。
小记:STL中的set函数,进行查找,量级同样是log(N),set是使用平衡二叉树实现的,左右子树高度相同。
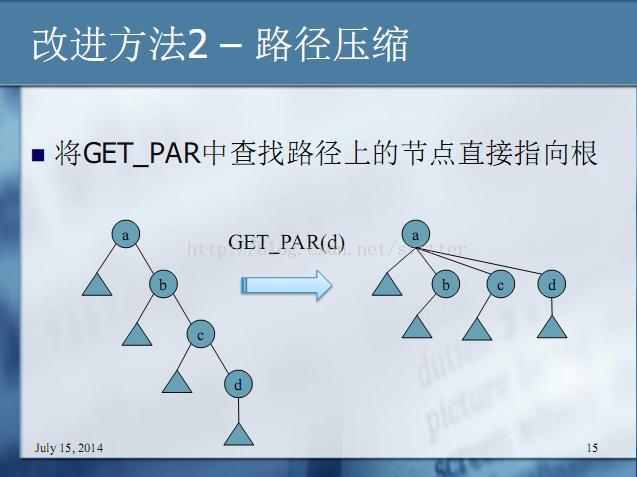
2.改进2:
路径压缩,即
以此来缩短路径。
示例题目:
POJ1611 The Suspects (并查集)
POJ2492 A Bug's Life (并查集)
POJ1182 食物链 (并查集)*新方法
POJ1988 CubeStacking (并查集)
POJ1291 This Sentence is False (并查集 || 哈希)
确定的有穷自动机。在编译原理中有所讲述。Compiler_词法分析_表驱动法_分析文件
3.Trie树
Trie图是一种特殊的DFA。通过遍历字符串来建立,可以由Trie构造出来。
KMP+Trie图即为AC自动机。
危险节点(终止节点,循环便利所有前缀节点,均为终止节点)。
关于时间复杂度:
层次代表长度,往上走的都是后缀,最多往下走一层,trie图中移动一层。
基础题目:HihoCoder——Trie树
三.数论,组合数学,博弈,群(置换群),数学问题
1.数论,组合数学
数论内容:扩展gcd,裴蜀定理,模线性方程,中国剩余定理,高斯消元法,线性筛素数,欧拉函数,欧拉定理。
1)扩展gcd与裴蜀定理
注意:d为公约数,直接加(L)表示(mod L),不再赘述。
gcd(a,b) = 1 说明 a,b互素。
au + bv = 1 ==> au + bv = gcd(a,b)
因为(a = d*a', b = d*b')
int gcd(int a, int b)
{
//b == 0 means that a is b's cd;
return b == 0 ? a : gcd(b, a%b);
}
int ex_gcd(int a, int b, int &u, int &v)
{
if(b == 0)
{
u = 1, v = 0;
return a;
}
/*
* prove:
* au + bv = d;
* (a - b)u + b(u + v) = d
* a' = a % b;
* a = b * t + a'
* a'u + b(tu + v) = d
* v' = b(tu + v)
* a'u + bv' = d
*/
int d = ex_gcd(b, b%a, v, u); //翻转u, v
v = v - a/b * u; //容易溢出
return d;
}
2 )模线性方程
ax = d (mod b) 可以转换成为 ax + by = d .
3)中国剩余定理
1.一般情况
n组数字(ai, bi),其中bi两两互素。
求x使得
x = a1 mod b1
x = a2 mod b2
...
x = an mod bn
类似思想有拉格朗日差值公式。
证明:
B = b1 * b2 * b3 ... *bi
ci = B / bi
mi * ci = 1 (bi)
ai* ci * mi = ai (bi)
...得证
x = a1b1m1 + a2b2m2 + ... anbnmn;
2.特殊情况
bi两两不互素,则化为一个式子。
~ x = a1 (b1)
~ x = a2 (b2)
~ x = a1 + b1 * u x = a2 + b2 * v
~ b1*u + b2*v = (a2 - a1) 化为裴蜀定理一般情况au+bv=d, d = gcd(a,b),有解当且仅当gcd(a,b) | (a1-a2)
4)高斯消元法
5)线性筛素数
减少筛的次数,只筛一次素数。
void getPrime(int n)//n为最大数
{
int num = 0;
memset(Prime, 0, sizeof(Prime));
memset(isPrime, 1, sizeof(isPrime));
for(int i = 2; i <= n; i ++)
{
if(isPrime[i])
Prime[num++] = i;
for(int j = 0; j < num && i * Prime[j] <= n; j++)
{
isPrime[i*Prime[j]] = 0;
if(i % Prime[j] == 0) break;
}
}
6 ) 欧拉函数,欧拉定理
欧拉函数
= n - n / pi = n ( 1 - 1/p1) ( 1 / p2) ... 相当于素因子展开 + 容斥原理
p为质因数
可以从(1 - 1/p1 - 1/p2 + 1/p1*p2)看出。
参考题目:hdu1286 找新朋友 (欧拉函数法)
欧拉定理:
a^φ(n) = 1 (mod n) => a^x = a ^ ( x mod φ(n) + φ(n)) (mod n) (不需要互素)
2.博弈
主要讨论了SP函数。
3.群
主要讨论了置换群的问题,在离散数学中有所涉及。着色定理可以有费马小定理推导出。
4.数学问题
杂题_POJ上的过桥问题
四.动态规划
递归一般转换方法。
递归函数有n个参数,就定义一个n维的数组,数组的下标是递归函数参数的取值范围,数组元素的值是递归函数的返回值,这样就可以从边界值开始,逐步填充数组,相当于计算递归函数值的逆过程。