Learning Theory
Empiricial Risk Minimization
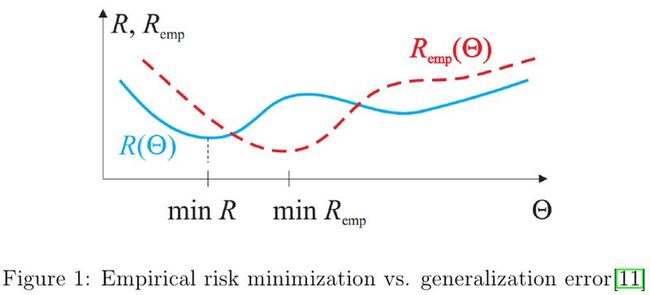
统计学习理论是整个机器学习到框架。试想我们学习的目的是什么呢?当然是为了具备用合理的方式处理问题的能力。统计学习理论要解决的问题就是基于数据找到一个预测函数。经验风险最小化(Empiricial Risk Minimization,ERM)[2]是统计学习理论中准则之一,常用于给出学习算法(learning algorithms)性能的理论边界。 假定给定两个数据空间\(X\)和\(Y\), 我们想学习到一个假设函数(hypothesis function)\(h:X\rightarrow Y\)。对于任意的\(x\in X\), 我们可用假设函数求得\(x\)在空间\(Y\)中对应的映射\(y\in Y\),即\(y=h(x)\)。假设\(X\)和\(Y\)之间存在联合概率分布\(P(x,y)\),注意在联合概率的假设下,\(x\)和\(y\)之间不存在单一映射关系。具体而言,即使给定\(x\),\(y\)依然是个随机变量,最合理的\(y\)就是使不确定性最小的:\(y=arg\underset{y\in Y}{\max}\;P(y|x)\)。如何衡量我们预测的结果好不好呢?损失函数(loss function)登场了,损失函数\(L(y,\hat{y})\)度量预测值\(\hat{y}\)与真实值\(y\)之间的差距,两者越相近,对应的损失也就越小。在二分类问题中,损失函数常定义为\(L(y,\hat{y})=I(y\neq\hat{y})\);在回归问题中,损失函数更倾向于\(L(y,\hat{y})=(y-\hat{y})^2\)。假设函数\(h(x)\)的风险(泛化误差)定义为损失函数的期望: \begin{equation} R(h)=\mathbb{E}\left[L(h(x),y)\right]=\int L(h(x),y)d P(x,y) \end{equation} 学习算法的终极目标是在假设集合\(\mathcal{H}\)中找到最优的假设函数\(h^{\star}\),使得风险\(R(h)\)最小: \begin{equation} h^{\star}=arg \underset{h\in\mathcal{H}}{\min}\;R(h) \end{equation} 绝大多数情形下,我们不知道概率分布\(P(x,y)\),使得学习算法无法计算\(R(h)\)。但是我们可以通过在\(P(x,y)\)上采样的方式来计算\(R(h)\)的近似值。假设我们从\(P(x,y)\)采样得到的\(m\)个独立同分布的样本组成训练集\(\mathcal{S}=\{(x^{(i)},y^{(i)})\}_{i=1}^m\),那么风险\(R(h)\)对应的近似值\(\hat{R}(h)\)只需在训练集上计算损失函数的均值即可: \begin{equation} \hat{R}(h)=\frac{1}{m}\sum_{i=1}^mL(h(x^{(i)},y^{(i)}) \end{equation} 其中\(\hat{R}(h)\)即为经验风险(empirical risk)。经验风险最小化准则阐述的规律就是使经验风险最小的假设函数对应实际的最优假设函数\(h^{\star}\)的近似值\(\hat{h}^{\star}\): \begin{equation} \hat{h}^{\star}=arg\underset{h\in\mathcal{H}}{\min}\;\hat{R}(h) \end{equation} 根据大数定理可知,在训练数据足够多的情况下(\(n\rightarrow\infty\)),经验风险是可以收敛到真实的泛化误差的。但在大多实际应用中,可用于训练模型的样本却往往非常有限。因此,在有限的训练数据情形下,使经验风险最小的假设函数,其对应的泛化误差不一定是最小的,即可能不是泛化能力最强的假设函数,如图1所示。
Probabilistic Inequalities
在展开学习理论之前,非常有必要简单回顾并证明一下相关的概率不等式,这是进一步讨论学习理论的基础。
定理一(Jensen's Inequality)[4]
假设\(X\)为随机变量,\(f:X\rightarrow\mathbb{R}\)为凸函数(convex),有 \begin{equation} f\left(\mathbb{E}[X]\right)\leq \mathbb{E}\left[f(x)\right] \end{equation} 如果\(f\)为凹函数(concave)则有相反的结论 \begin{equation} f\left(\mathbb{E}[X]\right)\geq \mathbb{E}\left[f(x)\right] \end{equation}
定理二(Markov's Inequality)[5]
假设\(X\)为非负的随机变量,对任意的\(t>0\),有 \begin{equation} P(X>t)\leq\frac{\mathbb{E}[X]}{t} \end{equation}
证明: \begin{equation} \begin{array}{rl} \mathbb{E}[X]&=\int_{0}^{+\infty}xp(x)dx=\int_{0}^{t}xp(x)dx+\int_{t}^{+\infty}xp(x)dx\\ &\geq \int_{t}^{+\infty}xp(x)dx \geq t\int_{t}^{+\infty}p(x)dx=tP(X>t) \end{array} \end{equation}
定理三(Chernoff Bound)[1]
假设\(X\)为随机变量,有 \begin{equation} P(X>\epsilon)\leq\underset{t\geq 0}{\inf}\exp(-t\epsilon)\mathbb{E}[\exp(tX)] \end{equation} 其中\(inf\)表示函数的最大下界。
证明: \begin{equation} \begin{array}{rl} P(X>\epsilon)&=P\left(\exp(X)>\exp(\epsilon)\right)\\ &=\underbrace{P\left(\exp(tX)>\exp(t\epsilon)\right)\leq\exp(-t\epsilon)\mathbb{E}[\exp(tX)]}_{Markov's \; inequality} \end{array} \end{equation}
定理四
假设随机变量\(X\in[a,b]\),\(\mathbb{E}[X]=0\),有 \begin{equation} \mathbb{E}[\exp(tX)]\leq\exp\left(\frac{t^2(b-a)^2}{8}\right) \end{equation}
证明: 在\(a\neq 0,b\neq 0\)时,我们可以将\(X\)表示成\(a\)和\(b\)的线性组合\(X=\alpha b+(1-\alpha)a\),其中\(\alpha=(X-a)/(b-a)\in[0,1]\)。对于凸函数\(f(x)=\exp(tx)\),如果我们将\(X\)视为一个Bernoulli分布的随机变量(即\(P(X=b)=\alpha,P(X=a)=1-\alpha\)),那么根据Jensen不等式,有 \begin{equation} f(X)=f(\alpha x+(1-\alpha)b)\leq\alpha f(x)+(1-\alpha)f(b) \end{equation} 将\(X=\alpha b+(1-\alpha)a\)带入上述不等式中,得 \begin{equation} \exp(tX)\leq\frac{X-a}{b-a}\exp(tb)+\frac{b-X}{b-a}\exp(ta) \end{equation} 在上式左右两边求期望值,结合\(\mathbb{E}[X]=0\),有 \begin{equation} \mathbb{E}[\exp(tX)]\leq-\frac{a}{b-a}\exp(tb)+\frac{b}{b-a}\exp(ta)=\exp(g(u)) \end{equation} 其中\(u=t(b-a)\),\(g(u)=-\theta u+\log(1-\theta+\theta\exp(u))\),\(\theta=-a/(b-a)\in(0,1)\)。 根据二阶Taylor展开公式,存在\(v\in(0,u)\)使得下式成立: \begin{equation} g(u)=g(0)+ug'(0)+\frac{u^2}{2}g''(v) \end{equation} 接下来,对\(g(u)\)求一阶倒数和二阶倒数 \begin{equation} g'(0)=-\theta+\frac{\theta\exp(u)}{1-\theta+\theta\exp(u)}\vert_{u=0}=0 \end{equation} \begin{equation} g''(v)=\frac{\theta\exp(v)}{1-\theta+\theta\exp(v)}\left(1-\frac{\theta\exp(v)}{1-\theta+\theta\exp(v)}\right)\leq\frac{1}{4} \end{equation} 该不等式成立,因为对任意\(s\in[0,1]\),有函数\(s(1-s)\leq\frac{1}{4}\)。将\(g(0)=0\),\(g'(0)=0\),\(g''(v)\leq 1/4\)和\(u\)带入Taylor展开式中,得到以下不等式: \begin{equation} g(u)=\frac{u^2}{2}g''(v)\leq\frac{u^2}{8}=\frac{t^2(b-a)^2}{8} \end{equation} 由上式可得 \begin{equation} \mathbb{E}[\exp(tX)]\leq\exp\left(\frac{t^2(b-a)^2}{8}\right) \end{equation} 我们可以验证,在\(a=b=0\)时,上述不等式仍然是成立的。
定理五(Hoeffding's Inequality)[3]
假设\(X_1,\cdots,X_n\)为\(n\)个相互独立的随机变量,且\(X_i\in[a_i,b_i]\),\(\bar{X}=\sum_{i=1}^nX_i/n\),则对任意的\(\epsilon>0\)有 \begin{equation} P\left(|\bar{X}-\mathbb{E}[\bar{X}]|>\epsilon\right)\leq 2\exp\left(\frac{2n^2\epsilon^2}{\sum_{i=1}^n(b_i-a_i)^2}\right) \end{equation}
证明:根据对称性、Chernoff边界定理、定理四以及随机变量间的相互独立性质,可推导出下式 \begin{equation} \begin{array}{rl} &P\left(|\bar{X}-\mathbb{E}[\bar{X}]|>\epsilon\right)\\ =&2P\left(\bar{X}-\mathbb{E}[\bar{X}]>\epsilon\right)\\ \leq& 2\underset{t\geq 0}{\inf}\exp(-t\epsilon)\mathbb{E}[\exp(t\bar{X})]\\ =& 2\underset{t\geq 0}{\inf}\exp(-t\epsilon)\mathbb{E}[\exp(t\sum_{i=1}^nX_i/n)]\\ =& 2\underset{t\geq 0}{\inf}\exp(-t\epsilon)\mathbb{E}[\prod_{i=1}^n\exp(tX_i/n)]\\ =& 2\underset{t\geq 0}{\inf}\exp(-t\epsilon)\prod_{i=1}^n\mathbb{E}[\exp(tX_i/n)]\\ \leq & 2\underset{t\geq 0}{\inf}\exp(-t\epsilon)\prod_{i=1}^n\exp(t^2(b_i-a_i)^2/(8n^2))\\ =& 2\underset{t\geq 0}{\inf}\exp(-t\epsilon+\sum_{i=1}^nt^2(b_i-a_i)^2/(8n^2)) \end{array} \end{equation} 为了得到尽可能接近真实值的上阶,我们还剩最后一步,即求出上式最右侧函数的最大下界。定义函数\(p:\mathbb{R}\rightarrow\mathbb{R}\)为 \begin{equation} p(t)=-t\epsilon+\sum_{i=1}^n\frac{t^2(b_i-a_i)^2}{8n^2} \end{equation} 很显然\(p(t)\)是一个二次函数,其最大下界可在极值点出取得: \begin{equation} p'(t)=-\epsilon+\frac{t\sum_{i=1}^n(b_i-a_i)^2}{4n^2}=0 \end{equation} 解上式可得 \begin{equation} t=\frac{4n^2\epsilon}{\sum_{i=1}^n(b_i-a_i)^2} \end{equation} 将\(t\)带入\(p(t)\)即可得Hoeffding不等式: \begin{equation} P\left(|\bar{X}-\mathbb{E}[\bar{X}]|>\epsilon\right)\leq 2\exp\left(-\frac{2n^2\epsilon^2}{\sum_{i=1}^n(b_i-a_i)^2}\right) \end{equation}
定理六(Union Bound)[8]
对于有限个事件\(A_1,A_2,\cdots,A_n\),有 \begin{equation} P\left(\bigcup_{i=1}^nA_i\right)\leq\sum_{i=1}^nP(A_i) \end{equation}
证明: 我们用归纳法来证明该定理。在\(n=1\)时,显然\(P(A_1)\leq P(A_1)\);假设在\(n=k\)时,\(P\left(\bigcup_i^kA_i\right)\leq\sum_{i=1}^nP(A_i)\)成立;那么在\(n=k+1\)时,结合\(P(A\cup B)=P(A)+P(B)-P(A\cap B)\),有 \begin{equation} \begin{array}{rl} P\left(\bigcup_{i=1}^{k+1}A_i\right)&=P\left(\bigcup_{i=1}^{k}A_i\right)+P(A_{k+1})-P\left(\bigcup_{i=1}^{k}A_i\cap A_{k+1}\right)\\ &\leq\sum_{i=1}^kP(A_i)+P(A_{k+1})=\sum_{i=1}^{k+1}P(A_i) \end{array} \end{equation} 综上所述,可知该定理成立。
Model complexity and Generalization Error
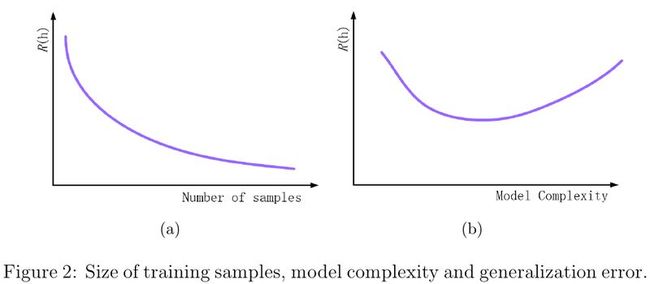
机器学习求解的假设函数不是单纯为了拟合已有的数据,其最终目标是准确预测未知数据的输出。经验风险最小化存在过拟合的风险,其目的在于找到一个可以很好与训练数据匹配的假设函数,而该假设函数不一定能预测未知数据的输出。如图2所示,训练数据的规模\(m\)、模型复杂度和泛化误差\(R(h)\)三者间存在一定的关系。我们如何避免过拟合?我们可以从两方面应对这个问题。 从图2(a)中可知,增加训练数据的规模有利于降低泛化误差。但也不是训练数据越多越好,因为当训练数据达到一定规模后,泛化误差的变化趋于平缓。那么一定的规模到底是个什么概念呢?这对应我们后面即将说明的算法的样本复杂度。观察图2(b),可知模型复杂度太大或者太小都会导致泛化误差过大。因此,另一个避免模型过拟合的方法就是控制模型复杂度。 机器学习领域有个警句,"Sometimes it's not who has the best algorithm that wins;it's who has the most data"。现在大数据也吵得火热,图2也可以帮助我们理解为什么大量的训练数据加上一般的模型产生的威力可能要强于少量的训练数据加上优秀的模型。但是呢,纵然现在有分布式计算作为支撑,过多的训练数据还是会带来很大的存储、通信和计算开销,但在有些情形下盲目增大训练数据的规模意义不大;另一方面,在某些领域想要获取足够多的训练数据不是那么容易的。在研究机器学习算法时,模型的复杂度是我们更为关心的问题。
The case of finite \(\mathcal{H}\)
我们用\(|\mathcal{H}|\)表示假设集合\(\mathcal{H}\)中包含的假设函数的数目,有限个假设函数组成假设集合\(\mathcal{H}=\{h_1,h_2,\cdots,h_{|\mathcal{H}|}\}\),根据经验风险最小化的原则,从假设集合\(\mathcal{H}\)中估计出的最优假设函数满足训练误差最小的条件: \begin{equation} \hat{h}=arg\underset{h_i\in\mathcal{H}}{\min}\hat{R}(h_i) \end{equation} 下面要证明的是使训练误差较小的假设函数\(\hat{h}\),其泛化误差也不至于太大。我们分两步完成这个证明:首先,对任意假设函数\(h\)而言,\(\hat{R}(h)\)都是\(R(h)\)的一个可靠的近似值;其次,给出\(\hat{h}\)的泛化误差\(R(\hat{h})\)的上界。 我们在样本空间内根据样本的概率分布\(\mathcal{D}\)进行采样,得到训练集\(\mathcal{S}=\{(x^{(i)},y^{(i)})\}_{i=1}^m\)。给定任意假设函数\(h_i\in\mathcal{H}\),定义服从Bernoulli分布的随机变量\(Z_j=I\{h_i(x^{(j)})\neq y^{(j)}\}\in\{0,1\}\),则\(Z_j\)表示\(h_i\)是否将样本\((x^{(j)},y^{(j)})\)误分类了,\(h_i\)的泛化误差\(R(h_i)=P(z_j=1)\)。因为所有样本都是从同一个概率分布中独立采样的,所以\(\{Z_j\}_{j=1}^m\)中的都是满足独立同分布的Bernoulli随机变量。\(h_i\)的训练误差形式为: \begin{equation} \hat{R}(h_i)=\frac{1}{m}\sum_{j=1}^mI\{h_i(x^{(j)})\neq y^{(j)}\}=\frac{1}{m}\sum_{j=1}^mz_j \end{equation} 显然\(\hat{R}(h_i)\)为\(m\)个独立同分布的Bernoulli随机变量的均值,且这些随机变量的期望值都为\(R(h_i)\)。根据Hoeffding不等式,得到如下规律: \begin{equation} P\left(|R(h_i)-\hat{R}(h_i)|>\gamma\right)\leq 2\exp(-2\gamma^2m) \end{equation} 上述规律说明:对特定假设函数\(h_i\)而言,在样本数目\(m\)足够大时,训练误差和泛化误差近似相等的概率可以非常大,这也证明了\(\hat{R}(h)\)都是\(R(h)\)的一个可靠的近似值。 但我们想要保证的不仅仅是这种近似的可靠性只对特定的假设函数成立,而是对假设集合\(\mathcal{H}\)中的所有假设函数都成立。现将事件\(A_i\)定义为\(|R(h_i)-\hat{R}(h_i)|>\gamma\),则由上一个结论可得\(P(A_i)\leq 2\exp(-2\gamma^2m)\)。 \begin{equation} \begin{array}{rl} &P\left(\exists h\in\mathcal{H}.|R(h_i)-\hat{R}(h_i)|>\gamma\right)\\ =&P(\bigcup_{i=1}^{|\mathcal{H}|}A_i)\\ \leq & \sum_{i=1}^{|\mathcal{H}|}P(A_i)\\ \leq & 2\sum_{i=1}^{|\mathcal{H}|}\exp(-2\gamma^2m)\\ =& 2|\mathcal{H}|\exp(-2\gamma^2m) \end{array} \end{equation} 上述事件的对立事件对应的概率为: \begin{equation} \begin{array}{rl} &P\left(\neg\exists h\in\mathcal{H}.|R(h_i)-\hat{R}(h_i)|>\gamma\right)\\ =&P\left(\forall h\in\mathcal{H}.|R(h_i)-\hat{R}(h_i)|\leq\gamma\right)\\ \geq & 1-2|\mathcal{H}|\exp(-2\gamma^2m) \end{array} \end{equation} 上式被成为一致性收敛(uniform convergence),因为这个边界值对\(\mathcal{H}\)中的所有假设函数都成立。由此可知,\(\mathcal{H}\)中的所有假设函数的训练误差与泛化误差偏离范围在\(\gamma\)以内的概率至少为\(1-2|\mathcal{H}|\exp(-2\gamma^2m)\)。 现在,我们已经得到了训练样本数目\(m\)、训练误差与泛化误差间的偏离上限\(\gamma\)及其发生最大偏差时的的概率下限\(1-2|\mathcal{H}|\exp(-2\gamma^2m)\)三者间的关系,在给定其中两个值的情况下我们可以推出第三个变量需要满足的条件。比如说,为了确保所有假设函数的训练误差和泛化误差间的偏差范围都在\(\gamma\)以内的概率至少为\(1-\delta\),至少需要多少个训练样本?这个问题对应的数学表述为: \begin{equation} P\left(\forall h\in\mathcal{H}.|R(h_j)-\hat{R}(h_j)|\leq\gamma\right)\geq 1-2|\mathcal{H}|\exp(-2\gamma^2m)\geq 1-\delta \end{equation} 求解上述不等式,可得训练样本数目\(m\)的下界: \begin{equation} m\geq\frac{1}{2\gamma^2}\log\frac{2|\mathcal{H}|}{\delta}=O\left(\frac{1}{\gamma^2}\log\frac{|\mathcal{H}|}{\delta}\right) \end{equation} 这条规律对我们是非常有用的,由此我们可以推测算法性能要达到某种水平,至少需要多少个样本就足够了,这也称为算法的样本复杂度(sample complexity)。一般而言,\(\log |\mathcal{H}|\)增长很慢,据CMU的Andrew Moore所说,\(\log |\mathcal{H}|\leq 30\)。样本数目太少不能保证训练出来的模型有较优的性能,样本数目也没必要太多太多,尤其在样本的收集比较困难的情况下,只要能在模型性能达到期望的效果,样本越少越好。 同样地,假设样本数目\(m\)和\(\delta\)都确定了,我们想知道假设集合\(\mathcal{H}\)中所有假设函数的训练误差和泛化误差间偏离程度\(\gamma\): \begin{equation} |R(h_j)-\hat{R}(h_j)|\leq\gamma\leq\sqrt{\frac{1}{2m}\log\frac{2|\mathcal{H}|}{\delta}} \end{equation} 接下来,我们即将给出\(\hat{h}\)的泛化误差上界。定义假设集合\(\mathcal{H}\)中的最优假设函数为: \begin{equation} h^{\star}=arg\underset{h\in\mathcal{H}}{\min}\;R(h) \end{equation} 由于\(h^{\star}\)训练误差小于\(\hat{h}\),结合\(|R(h)-\hat{R}{h}|\leq\gamma\),可得到\(\hat{h}\)的泛化误差上界: \begin{equation} R(\hat{h})\leq\hat{R}(\hat{h})+\gamma\leq\hat{R}(h^{\star})+\gamma\leq R(h^{\star})+2\gamma \end{equation} 上式说明,训练误差最小的假设函数\(\hat{h}\)的泛化误差顶多比假设集合中最优的假设函数\(h^{\star}\)高\(2\gamma\),即: \begin{equation} R(\hat{h})\leq\left(\underset{h\in\mathcal{H}}{\min}\;R(h)\right)+2\sqrt{\frac{1}{2m}\log\frac{2|\mathcal{H}|}{\delta}} \end{equation} 如果扩大模型的复杂度,即假设空间增大为\(\mathcal{H}'\supset\mathcal{H}\)。在\(\mathcal{H}'\)中,我们可能找到泛化误差更小的假设函数,因此第一项不可能增大;\(\mathcal{H}'\)中假设函数的数目\(k\)增大,必然使得第二项增大。 根据如下关系: \begin{equation} R(\hat{h})\leq \hat{R}(\hat{h})+\sqrt{\frac{1}{2m}\log\frac{2|\mathcal{H}|}{\delta}} \end{equation} 我们可以总结出如下规律:在\(|\mathcal{H}|\)有限的情况下,只要样本数目\(m\)足够大,就有\(R(\hat{h})\approx \hat{R}(h)\);此时若有\(\hat{R}(\hat{h})\approx 0\),必然有\(R(\hat{h})\approx 0\),即通过经验风险最小化得到的最优假设函数是可靠的。但实际情况并非如此简单:如果\(|\mathcal{H}|\)有限,在大多数情况下我们无法保证从\(\mathcal{H}\)中选择出来的假设函数的经验风险趋近于0(少数时候可以碰巧找到经验风险为0的假设函数),此时\(\hat{h}\)的泛化误差可能无法令人满意;如果\(|\mathcal{H}|\)趋于无限,我们虽可以保证\(\hat{R}(\hat{h})\approx 0\),但根据上式又无法得到\(R(\hat{h})\approx \hat{R}(h)\),使得无法确保\(\hat{h}\)的泛化误差足够小。在\(|\mathcal{H}|\)趋于无限时,是否真的无法保证\(R(\hat{h})\approx \hat{R}(h)\)呢?请看下面\(|\mathcal{H}|=\infty\)的情况。
The case of infinite \(\mathcal{H}\)
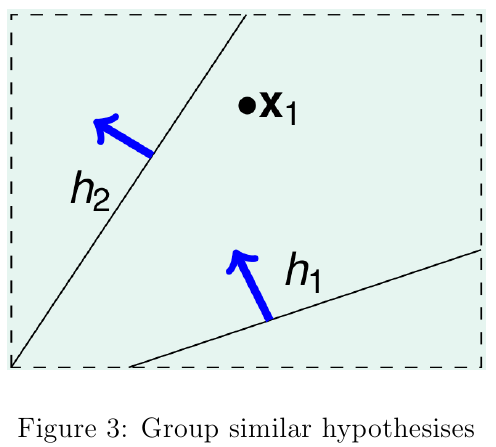
为什么前面推导出的\(R(\hat{h})\)的泛化误差的上界在\(|\mathcal{H}|=\infty\)时没多少用呢?因为在推导过错中用到了union bound的性质,而且union bound定理中给出的上界是在假设所有假设函数\(h_i\)之间都相互独立的前提下给出的。在实际情况中,\(\mathcal{H}\)有不少假设函数都是相似的。任意相似的两个假设函数\(h_i\approx h_j\),两者有很多地方都是重叠的,也就说\(\hat{R}(h_i)=\hat{R}(h_j)\)的概率很大。显然,\(h_i\)和\(h_j\)不可能相互独立,此时还用相互独立的假设计算union bound会把重叠部分重复计算多次,致使给出的上界太过松弛。举个简单的例子,假设\(\mathcal{H}\)为二维平面上所有直线的集合,显然\(|\mathcal{H}|=\infty\)。如图3中的\(x_i\)看来,二维平面中所有假设直线只有两种,在\(x_1\)上面或下面的直线。
既然如此,我们能否找到一种策略,将所有相似的假设函数归为有限的若干组呢?为了说明这个问题,下面我们简要介绍VC维。
VC Dimension
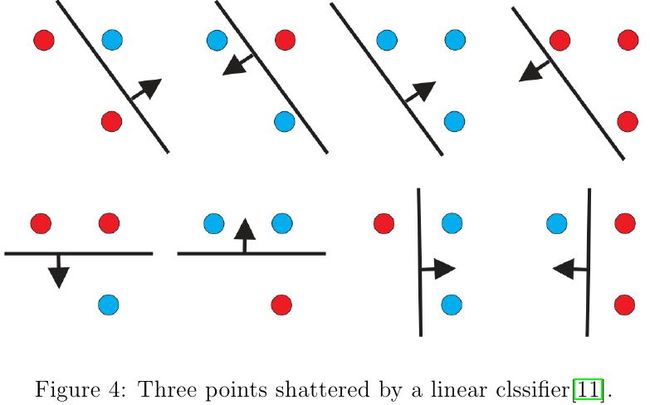
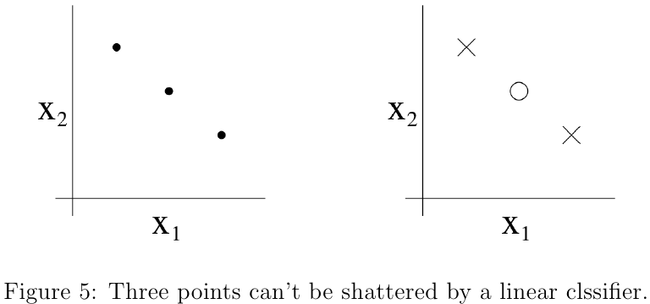
VC维(Vapnik-Chervonenkis dimension)[9]用于度量分类算法的复杂度。介绍VC维之前,先引入shatter(分散)这个概念。给定\(n\)个数据组成的集合\(\mathcal{X}=\{x^{(1)},x^{(2)},\cdots,x^{(d)}\}\),若对任意的标签集合\(\mathcal{Y}=\{y^{(1)},y^{(2)},\cdots,y^{(d)}\}\),都存在假设函数\(h\in\mathcal{H}\)可以完全正确分类,即\(h(x^{(i)})=y^{(i)}\)对\(\mathcal{X}\)中的所有数据都成立,则称\(\mathcal{H}\)可以分散\(\mathcal{X}\)。假设集合\(\mathcal{H}\)的VC维\(VC(\mathcal{H})\)定义为\(\mathcal{H}\)可以分散的集合的能包含的数据的最大数目;若\(\mathcal{H}\)足以分散任意大的集合,则\(VC(\mathcal{H})=\infty\)。需要注意的是,为了证明\(VC(\mathcal{H})\)至少为\(d\),我们只需要找到一个包含\(d\)个数据的集合能被\(\mathcal{H}\)分散即可;为了证明\(VC(\mathcal{H})\)最多为\(d\),我们要证明不存在包含\(d+1\)个数据的集合能被\(\mathcal{H}\)分散。 为了更为直观解释VC维的概念,我们以只包含线性分类器(即感知机,Perceptron)的\(\mathcal{H}\)在二维平面中的情况为例进行说明。在图4中,无论三个数据的标签如何变化,总能找到线性分类器实现无误差的分类。但在图5中,三点共线,线性分类器无法完全正确处理任意的分类任务。除此之外,对于包含至少4个数据的集合,再也无法在\(\mathcal{H}\)中找到可以完美分类的线性分类器。由此可见,\(\mathcal{H}\)能分散的集合最多只能包含三个数据,因此\(VC(\mathcal{H})=3\)。实际上,在\(d\)维空间里,线性分类器的VC维是\(d+1\)。看到这里,我们可能会非常气愤,好不容易抽出时间学习VC维,竟然被告知\(d\)维空间中的线性分类器顶多可以完全正确对\(d+1\)个数据正确分类,要它有何用?值得庆幸的是,现实世界的变化还是趋于平滑的,相邻的数据大多时候都属于相同类别,并不需要处理所有数据都是任意类别的情形。所以即使是VC维较小的分类器也是有用武之地的。
在统计学习理论中,VC维可用于给出分类模型的泛化误差的概率性的上界,并且该上界独立于样本的分布情况。如果分类模型集合\(\mathcal{H}\)对应的VC维为\(d\),以经验风险最小化为最优准则,经过\(m\)个服从独立同分布的数据训练后得到分类模型的\(\hat{h}\in\mathcal{H}\),\(\hat{h}\)的训练误差和泛化误差间的关系为: \begin{equation} P\left(R(\hat{h})\leq \hat{R}(\hat{h})+\sqrt{\frac{d}{m}\left(\log\frac{2m}{d}+1\right)+\frac{1}{m}\log\frac{4}{\delta}}\right)\geq 1-\delta \end{equation} 其中,带根号的那一项我们在此称之为VC置信度(也可视为模型复杂度对应的惩罚项)。具体的证明过程本想亲自推导一遍的,只是看了Vapnik的大作后顿时有了力不从心的感觉,目前肯起来太吃力,所有有兴趣的人士请参见[12,13]。 VC维可被有效应用于为线性分类器的泛化误差确定一个上界,SVM就是一个成功的应用典范。但其他场合下也许行不通,我们可以用以下三中情形来简单说明:
- 对于诸如神经网络等非线性模型,无法较为准确估计对应的VC维;
- 对于KNN(k=1)和采用高斯核函数的SVM模型等,VC维是无穷的;
- 上界有时不能提供任何指导意义,比如分类错误率的上界大于1时。
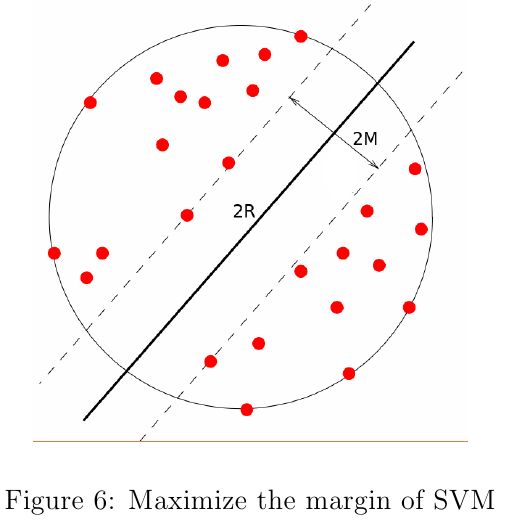
假设函数的VC维越大,表明其模型越复杂,对应的表达能力也越强!复杂模型的经验风险很小,同时也会因过于复杂带来较大的惩罚成分。如果最后泛化误差的上界增大,意味着泛化误差很小的概率越来越小,模型不稳定的几率会大大增加。奥卡姆剃刀(Occam's razor)原理提倡在多个具有处于竞争地位的可得出相同结论的理论中选择最简单的那个。换到我们这个语境中,可以理解成,在经验风险最小的若干个假设函数中,优先选择复杂度最低的模型。顺带提一下,为什么SVM要选择间隔最大的超平面?其实这背后也是和VC维有关系的。如图6所示,在\(n\)维空间里,如果所有数据点都可用一个半径至少为\(R\)的球面包围,超平面间的几何间隔为\(2M\),那么SVM的VC维的上界为[12]: \begin{equation} VC(\mathcal{H})\leq\min\left\lbrace\lceil\frac{R^2}{M^2},n\rceil\right\rbrace+1 \end{equation} 由上式可知,最大化几何间隔实际上实在降低SVM的VC维;此外,对线性可分的数据而言,这些超平面对应的经验风险为0,所以最大化几何间隔也是在直接降低泛化误差的上界。我以前经常在想,SVM的泛化性能和支持向量的数目是否有关系呢?这次我终于得到答案了。如果我们用留一法对SVM进行交叉验证,那么还有一个实际风险的上界[10]: \begin{equation} \mathbb{E}[P(error)]\leq\frac{\mathbb{E}[Number\;of\;support\;vectors]}{Number\;of\;training\;samples} \end{equation} 其中\(\mathbb{E}[P(error)]\)是在\(m-1\)个样本上训练后用剩下的一个样本测试得到的风险期望,\(\mathbb{E}[Number\;of\;support\;vectors]\)是支持向量的期望值。这个上界的产生是出于这样的一个思想:仅仅支持向量的变化才会引起超平面的变动,致使在最坏的情况下所有的支持向量都被误分类。但是据[10]指出:很多情形下即使支持向量数目减少了,实际的误差也还是会增大。所以,该上界不能提供准确的错误信息。即便如此,我们却可以根据这个现象得出一个结论:支持向量的数目不能作为衡量SVM泛化性能的指标。
那么在实际应用中,我们又如何选择合适的模型?模型选择[6]方法很多,大家最为熟悉的交叉验证(Cross Validation)就是其中之一。下面只简要介绍结构风险最小化的内容。
Structure Risk Minimization
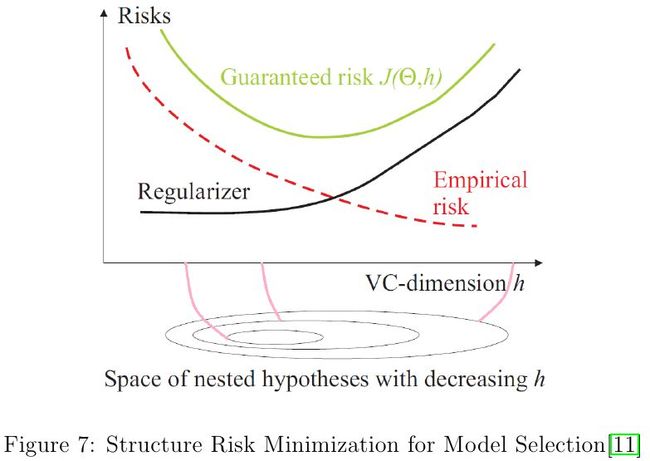
在机器学习中,我们必须根据有限的训练数据选择一个泛化模型(假设函数)来完成后续的预测任务,而选出来的这个泛化模型很有可能存在过拟合问题,即在训练数据上能很好拟合数据,但是在新数据上的预测结果却非常糟糕。结构风险定义为经验风险与VC置信度之和,构成了泛化误差的上界。结构风险最小化(Structure Risk Minimization, SRM)[7]通过在模型复杂度和训练数据上的拟合程度之间寻找一个平衡点,以解决过拟合问题,这也是VC维的一个应用场合。 结合图7,我们将结构风险最小化的步骤简要描述为如下四步:
- 根据先验知识选择一种类型的假设函数形成假设集合\(\mathcal{H}\),比如\(n\)次多项式或者有\(n\)个隐含结点的三层神经网络;
- 根据模型复杂度(VC维)递增的顺序将\(\mathcal{H}\)划分成若干逐层嵌套的假设集合\(\mathcal{H}_1\subseteq\mathcal{H}_2\subseteq\mathcal{H}_3\subseteq\cdots\subseteq\mathcal{H}\),比如\(\mathcal{H}_t\)可以是对应\(t\)次多项式的假设函数集合;
- 依次在每个\(\mathcal{H}_t\)上以经验风险最小化为原则选择假设函数\(\hat{h}_t\in\mathcal{H}_t\);
- 选择使泛化误差上界(经验风险+VC置信度)最小的模型为最优模型,在上界相同的情形下优先选择复杂度最低的模型。
References
[1] Chernoff bound. http://en.wikipedia.org/wiki/Chernoff_bound.
[2] Empirical risk minimization. http://en.wikipedia.org/wiki/Empirical_risk_minimization.
[3] Hoeffding’s inequality. http://en.wikipedia.org/wiki/Hoeffding’s_inequality.
[4] Jensen’s inequality. http://en.wikipedia.org/wiki/Jensen’s_inequality.
[5] Markov’s inequality. http://en.wikipedia.org/wiki/Markov_inequality.
[6] Model selection. http://en.wikipedia.org/wiki/Model_selection.
[7] Structural risk minimization. http://www.svms.org/srm/.
[8] Union bound. http://en.wikipedia.org/wiki/Boole’s_inequality.
[9] VC dimension. http://www.svms.org/vc-dimension/.
[10] Christopher JC Burges. A tutorial on support vector machines for pattern recognition. Data mining and knowledge discovery, 2(2):121–167, 1998.
[11] Vapnik-chervonenkis learning theory. http://cmp.felk.cvut.cz/~hlavac/TeachPresEn/31PattRecog/27VapnikChervonenkis.pdf